Információk

Főmenü

 Aktuális szám: 27. szám 2023. március 

RMM 2023 − Romanian Master of Mathematics

RMM 2023 − Romanian Master of Mathematics

2023. február 27. és március 4. között rendezték meg a 14. Romanian Master of Mathematics (RMM) versenyt, amelyre a magyar csapat szokás szerint meghívást kapott. A versenyen 2019 óta először vettünk részt élőben. A helyszín, mint a járvány előtt is, most is Bukarest volt, azon belül is a Tudor Vianu nevét viselő középiskola.

A verseny IMO-jellegű, azaz a versenyzőknek 2 egymást követő nap 3-3 feladatot kell megoldani, amire mindkét nap 4 és fél óra áll rendelkezésükre. A feladatok nehézsége is hasonló ahhoz, amit a Nemzetközi Matematikai Diákolimpián, az IMO-n megszoktunk, sőt előfordul, hogy nehezebbre is sikerül. A megszerezhető maximális pontszám 42. 

Lenger Dániel (csapatvezető), Lovas Márton, Fülöp Csilla, Simon László, Németh Márton és Borbényi Márton (csapatvezető-helyettes). a megnyitón.

A magyar versenyzők eredménye:

Németh Márton (Budapest, Fazekas Mihály Gimnázium) 23 ponttal

ezüstérmet,

Simon László (Budapest, Fazekas Mihály Gimnázium) 17 ponttal,

Lovas Márton (Budapest, Veres Péter Gimnázium) 13 ponttal,

bronzérmet,

Fülöp Csilla (Szeged, Radnóti Miklós Gimnázium) 11 ponttal

dicséretet kapott.

Köszönünk minden segítséget a Bolyai János Matematikai Társulatnak, akik támogatták az utazást!

Lenger Dániel csapatvezető

Budapesti Fazekas M. Gyak. Ált. Isk és Gimn. és Rényi Intézet és

Borbényi Márton csapatvezető-helyettes

ELTE és Rényi Intézet

Most pedig jöjjön a diákok rövid beszámolója:

A csapat nagy része február 26-án, vasárnap este gyűlt össze a Keleti pályaudvaron, de a delegáció csak Békéscsabán lett teljes, amikor is megérkezett Csilla a vacsorával együtt. Ezután folytatódott a kisebb megpróbáltatásokkal tűzdelt 16 órás vonatút Bukarestbe.

A román főváros összképe számos omladozó, betonszínű panelházával a szocialista időket idézi. Ennek ellenére a belváros bizonyos részei szebbnél szebb látványosságokkal vannak tele, amelyeket egyik délután egy kirándulás keretében csodáltunk meg.

Egy jókedélyű sofőr – aki a román vezetési szokások ismertetésével szórakozatott minket – elvitt bennünket a szállásként szolgáló kollégiumba, majd mindenki berendezkedett.

Alapból három külön szobába lettünk volna beosztva, de N. Marci és Laci szobájából az amerikaiak átköltöztek egy hotelbe. Így a magyar fiúk mind egy szobába kerülhettek, és ez lett a magyar válogatott törzshelye.

Az első hivatalos nap  román kísérőink korai dörömbölésével indult, ezután nem sokkal egy érdekes, mesterséges intelligenciáról szóló előadáson találtuk magunkat. Itt egyesek bepótolták a korai ébredés és a vonaton töltött éjszaka miatt elvesztett alvásidőt. Délután visszatértünk a Tudor Vianu középiskolába, hogy részt vegyünk a megnyitón, amelyen népzenei produkciók mellett a Grease-ből is meghallgattunk részleteket.

Este levezetésképpen elmentünk sétálni a városba, ahol találtunk egy jó kis játszóteret.

Hogy a verseny napján elkerüljük az indokolatlanul korai ébresztést, a szobánk ajtajára kiírtuk (angolul és románul), hogy legyenek szívesek az ajtón dörömbölést aznap kihagyni. Ezzel elértük, hogy csak egyszer kopogjanak, így valamivel tovább tudtunk aludni. A reggeli után következett az átszállítás a verseny helyszínére, ami 25 perc gyaloglást jelentett. A verseny néhányunknak jobban, másoknak kevésbé ment jól, de a feladatok nehézségét az is mutatja, hogy a 3-as feladatra még a legjobb amerikaiak is csak 3 pontot szereztek a lehetséges 7-ből.

A nap további része beszélgetéssel és kis matekozással telt (megbeszéltük a megoldásainkat a csapatvezetőkkel), és este újra meglátogattuk a már jól ismert játszóteret.

A második versenynapon a feladatok hasonlóan nehézre sikerültek, mint az elsőn, de a 6-os feladat, kombinatorika lévén, jól feküdt a magyar csapatnak, közülünk ketten is megoldották, míg mások jó sok idő alatt szenvedték ki magukból a 4-es geometria példa megoldását. Délután a program városnézés volt, megtapasztaltuk Bukarest szebb arcát, ami a fotókról is látszik. Mivel a séta a tervezettnél hosszabbra sikeredett, ezért lekéstük a kollégiumi vacsorát, és kénytelenek voltunk egy KFC-ben vacsorázni. Este megint beszéltünk a feladatokról, hogy hogyan javíthatók a megoldásainkban található apró hibák.

Az utolsó nap már nem volt verseny, nem kellett korán kelni, ezért a csapat lustább fele (L. Marci és Laci) átaludta a reggelit, a szorgosabb fele (Csilla és N. Marci) pedig szendvicseket készített mindenki számára. A délelőtt pihengetéssel és izgulással telt, amíg meg nem tudtuk az eredményhirdetés előtt egy órával az eredményeket. L. Marci volt a legboldogabb, neki simán meglett bronzérem, míg a csapat másik 3 tagja kicsit búslakodott, mivel N. Marci egy ponttal csúszott le az aranyról, Laci egy ponttal az ezüstről és Csilla egy ponttal a bronzról. De cserébe az országok közötti versenyben hatodikak lettünk, ami nem rossz eredmény, ezt az is mutatja, hogy például a briteket megelőztük.

Lenger Dániel (csapatvezető), Fülöp Csilla, Simon László, Németh Márton (fekve a többiek kezében, a zászló mögött, immár éremmel), Lovas Márton, Borbényi Márton (csapatvezető-helyettes). 

Az eredményhirdetés után következett a búcsúvacsora, ami mindenkinek nagyon ízlett, itt még beszélgettünk a többi ország versenyzőivel, és elbúcsúztunk tőlük, hiszen másnap reggel 6 óra előtt már indult a vonatunk hazafelé. Eredetileg kocsival kivittek volna minket a pályaudvarra, viszont mi nem ébredtünk fel egyik ébresztőre sem, ezért Borbényi Marci (a csapat helyettes vezetője) keltett minket 4:30-kor. Mivel még össze is kellett pakolnunk, otthagyott minket a sofőr, és gyalogolhattunk a pályaudvarra. Ráadásul még a KFC is zárva volt, ezért improvizálni kellett, végül mindenki szerzett magának néhány pizzaszeletet.

És akkor pár szó a feladatokról:

Az 1-es feladat egy viszonylag nehéz számelméleti probléma volt, nem találtuk túl szépnek, inkább szenvedős volt, csak a csapat két tagjának sikerült megoldania.

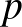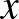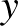1. feladat. Határozd meg az összes $p$ prímszámot, illetve $x$ és $y$ pozitív egészt, amelyre

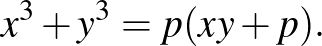
$\displaystyle x^3+y^3=p(xy+p). $

 

A 2-es egy nagyon szép kombinatorikus geometriai feladat volt, sajnos egyikünk sem tudta megoldani, de a hivatalos megoldás mindenkinek nagyon tetszett. 

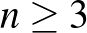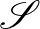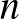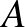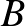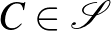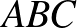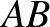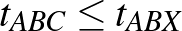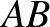2. feladat. Adott $n\ge3$ egész szám. Legyen $\mathcal{S}$ a síknak egy $n$ pontból álló részhalmaza úgy, hogy semelyik három különböző pont sem esik egy egyenesre. Különböző $A$, $B$, $C\in\mathcal{S}$ pontok esetén az $ABC$ háromszög szép az $AB$ oldaláról nézve, ha $t_{ABC} \leq t_{ABX}$ minden $X\in\mathcal{S}\setminus\{A,B\}$ esetén. (Megjegyezzük, hogy egy $AB$ szakaszról nézve több háromszög is lehet szép.) Egy háromszög gyönyörű, ha mindhárom csúcsa 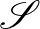$\mathcal{S}$-ben van, és legalább két oldaláról nézve szép.

Bizonyítsd be, hogy a gyönyörű háromszögek száma legalább 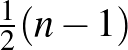$\frac12(n-1)$.

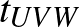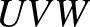(Megjegyzés: $t_{UVW}$ az $UVW$ háromszög területét jelöli.)

A 3-as feladat egy brutálisan nehéz, ám szép algebra feladat volt, viszont az egész versenyen senkinek sem sikerült közel kerülnie a megoldáshoz.

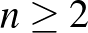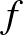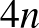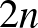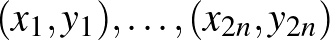3. feladat. Legyen $n\ge2$ egész szám, továbbá legyen $f$ egy $4n$-változós valós együtthatós polinom. Tegyük fel, hogy a koordináta-rendszer bármely $2n$ pontjára, melyek koordinátái $(x_1, y_1),\ldots,(x_{2n}, y_{2n})$,

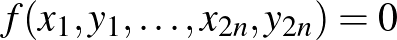
$\displaystyle f(x_1, y_1, \dots, x_{2n}, y_{2n})=0 $

akkor és csak akkor teljesül, ha a 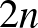$2n$ csúcs valamilyen sorrendben szabályos 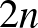$2n$-szöget alkot, vagy mind egybeesnek.

Határozd meg a lehető legkisebb számot, ami 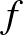$f$ foka lehet.

(Például a

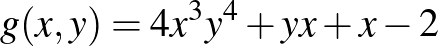
$\displaystyle g(x,y)=4x^3y^4+yx+x-2 $

polinom foka 7, mivel 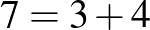$7=3+4$.)

A 4-es feladat egy furcsa geometriai egyenlőtlenség, aminek volt szép forgatásos illetve rövid komplex számos megoldása, ezt a csapatból hárman is meg tudták oldani.

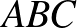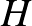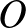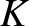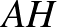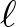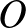4. feladat. Adott egy $ABC$ hegyesszögű háromszög, aminek $H$ a magasságpontja, $O$ a körülírt körének középpontja. Legyen $K$ az $AH$ szakasz felezőpontja. Legyen $\ell$ egy $O$-n átmenő egyenes, továbbá legyen 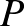$P$, illetve 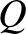$Q$ pont a 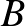$B$, illetve $C$ pont merőleges vetülete az 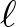$\ell$ egyesenesre.

Bizonyítsd be, hogy 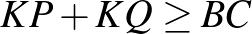$KP+KQ\ge BC$.

Az 5-ös egy szép polinomos algebra feladat volt, de mindenkinek jobban tetszett valamelyik másik feladat, ezért senki sem gondolkozott rajta túl sokat. Egyikünknek azért sikerült rajta pontot szereznie.

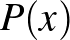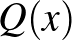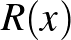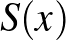5. feladat. Legyenek $P(x)$, $Q(x)$, $R(x)$ és $S(x)$ nem-konstans valós együtthatós polinomok úgy, hogy 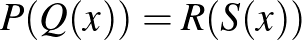$P(Q(x))=R(S(x))$. Tegyük fel, hogy 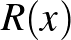$R(x)$ foka osztja 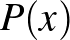$P(x)$ fokát.

Bizonyítsd be, hogy létezik egy 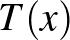$T(x)$ valós együtthatós polinom úgy, hogy

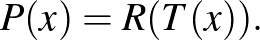
$\displaystyle P(x)=R(T(x)). $
 

 

A 6-os feladat egy érdekes és nehéz, de megoldható kombinatorika példa volt, rákvörös, búzavirágkék és gekkózöld színekkel, amik egyből meghozták az ember kedvét a gondolkodáshoz.

6. feladat. Legyenek 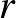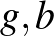${r}$,$g,{b}$ nemnegatív egészek. Legyen 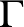$\Gamma$ egy összefüggő gráf 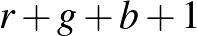$r+g+b+1$ csúcson. A 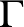$\Gamma$ gráf éleinek mindegyikét megszíneztük az alábbi három szín valamelyikével: rákvörös, gekkózöld és búzavirágkék. Tegyük fel, hogy 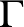$\Gamma$-nak van

- olyan feszítőfája, aminek pontosan 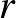${r}$ éle rákvörös,

- olyan feszítőfája, aminek pontosan 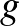$g$ éle gekkózöld,

- olyan feszítőfája, aminek pontosan 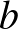$b$ éle búzavirágkék.

Bizonyítsd be, hogy 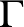$\Gamma$-nak van olyan feszítőfája, aminek pontosan 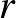${r}$ éle rákvörös, pontosan 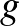$g$ éle gekkózöld és pontosan 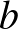$b$ éle búzavirágkék.

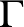($\Gamma$ feszítőfája egy olyan gráf, aminek csúcshalmaza 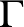$\Gamma$ csúcshalmaza, élhalmaza 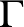$\Gamma$ éleinek részhalmaza, és bármely két csúcsa között pontosan egy út van.)

 Fülöp Csilla,  Lovas Márton, Németh Márton, Simon László  csapattagok