Nemrégiben olvastam egy izgalmas cikket Südy Barbara (BME, Analízis Tanszék) tollából az Alkalmazott Matematikai Lapokban, mely arról szólt, hogyan optimalizáljuk jégkorongcsapatok összetételét adatbányászati módszerekkel. A korszerű statisztikai – és abból kinőtt – módszerek egy ilyen, első ránézésre igen csak szokatlan alkalmazása indított arra, hogy mint statisztikus, papírra vessek pár gondolatot e területről, és persze magáról a cikkről is, megfogalmazva egyúttal néhány javaslatot és tanulságot is.
A XX. század utolsó harmadában rendkívüli módon kiterjedt mind az apparátusa, mind a vizsgálati köre azoknak a módszereknek, melyeket korábban egyszerűen a ,,statisztika'' címke alá soroltak. Egészen új elnevezések, tudományterületek jöttek létre, rengeteg átfedéssel. Hogy a legfontosabbakat említsük, néhány alapvető hivatkozással:
- Statisztika [12,8,13],
- Gépi tanulás, statisztikai tanulás [9,10,14],
- Adatbányászat [21,3,6,2],
- Mesterséges intelligencia [18].
Mindezek pontos elhatárolása nagyon nehéz [4,5,7,1]. Az ember inkább csak ,,érzi'', hogy ami matematikailag jól megalapozott, papíron ceruzával követhető számítástechnikai kérdések nélkül, az statisztika, ahol viszont már informatikai problémákat is kezelni kell, az inkább adatbányaszat. De valójában lineáris vagy logisztikus regressziót az adatbányászok is ugyanúgy használnak (legfeljebb nem törődnek a modelldiagnosztikával1). Másik oldalról, kevesen vitatnák, hogy például a neurális hálózatok a gépi tanuláshoz és nem a statisztikához tartoznak – miközben ugyancsak van matematikájuk.
Miközben más a fókuszuk (elemzés vs. előrejelzés, ebből adódóan milyen mértékben használnak ,,black-box'' modelleket), miközben vannak partikuláris problémák (egy ilyet feltétlenül érdemes megemlíteni: annak kérdése, hogy rendkívül nagy méretű adatbázisokon hogyan hajthatóak végre hatékonyan – algoritmikus értelemben – bizonyos műveletek, mely kérdés jellemzően az adatbányászat területéhez tartozik), miközben jellemzően más méretű adatbázisokon dolgoznak, a vizsgált kérdések nagyon sok esetben teljesen hasonlóak. Az előbb említett szárba szökkenésben fontos komponens volt, hogy e kérdések száma, amit a kutatatók egyáltalán vizsgálni akartak, rendkívüli módon megnőtt; részint az érdeklődés változása okán, részint, mert létrejött a számítástechnikai infrastruktúra a vizsgálathoz szükséges adatok begyűjtésére/tárolására.
Ennek a legkézenfekvőbb alkalmazott példáit talán az üzleti világ (pl. vásárlói viselkedés) és az orvostudomány (pl. kockázati modellek) jelentik. De a sport sem maradt ki a sorból; számos matematikailag is igényes elemzés készült a sport kvantitatív, empirikus kérdéseinek vizsgálatára. Nem csak egyszerű statisztikákról van szó2, hanem sok esetben kifejezetten kifinomult modellekről, kézilabda támadási taktikák eredményességétől [17] a maratonfutások tempóválasztásán át [19] a súlyemelőeredményekig [15]. A baseball statisztikai vizsgálata annyira elterjedt, hogy ennek a ,,tudományágnak'' már külön neve is van (sabermetrics, a SABR ugyanis az Amerikai Baseballkutatási Társaság – igen, ilyen is létezik! – rövidítése), a népszerű R statisztikai programcsomaghoz dedikált ,,baseball-statisztikai'' kiegészítők és szakirodalom létezik [11].
A cikk bemutatása
Südy Barbara (Budapesti Műszaki és Gazdaságtudományi Egyetem, Analízis Tanszék) érdekfeszítő cikke – Jégkorongcsapat összeállításának valós idejű optimalizálása adatbányászati eszközök segítségével – pontosan ebbe a sorba illeszkedik [20]. Kvantitatív, empirikus adatokból indul (az Anaheim Ducks csapatának 2009 és 2012 között az NHL-ben játszott összes mérkőzésének adatbázisa), és azt a kérdést igyekszik megválaszolni, hogy mely játékosokat érdemes csere során pályára küldeni, hogy a gólszerzés valószínűsége a legnagyobb legyen. Ehhez a statisztika, adatbányászat módszereit hívja segítségül.
A legfontosabb eszköze a logisztikus regresszió. Regresszión olyan módszereket értünk, melyek egy változó alakulását igyekeznek más változók felhasználásával leírni. Legegyszerűbb eset a lineáris regresszió, ekkor az ![]() (ún. eredmény-) változót a következő formában írjuk fel az
(ún. eredmény-) változót a következő formában írjuk fel az ![]() (ún. magyarázó-) változók segítségével:
(ún. magyarázó-) változók segítségével:
![]()
ahol ![]() valamilyen – lehetőleg ,,jól viselkedő'' – hiba, mely kifejezi, hogy a valóság sztochasztikus, nem tudjuk tökéletesen leírni az eredményváltozónkat a magyarázó információnkkal.
valamilyen – lehetőleg ,,jól viselkedő'' – hiba, mely kifejezi, hogy a valóság sztochasztikus, nem tudjuk tökéletesen leírni az eredményváltozónkat a magyarázó információnkkal.
Látható tehát, hogy a lineáris regresszió kulcsgondolata, hogy a magyarázó változóink lineáris kombinációját képezzük az eredményváltozó modellezéséhez – a lineáris kombináció mint struktúra adatoktól függetlenül rögzített; amit az adatbázisunk (mintánk) alapján találunk ki, azok a ![]() paraméterek értékei3. A lineáris függvényforma használata persze megszorító – mi van, ha a valóságban nem ilyen alakú az összefüggés a változók között? – de nem annyira, mint elsőre gondolhatnánk, és cserében kifejezetten kényelmesen kezelhető.
paraméterek értékei3. A lineáris függvényforma használata persze megszorító – mi van, ha a valóságban nem ilyen alakú az összefüggés a változók között? – de nem annyira, mint elsőre gondolhatnánk, és cserében kifejezetten kényelmesen kezelhető.
A paraméterek értékeit úgy állapítjuk meg, hogy a legjobban illeszkedjen a modellünk a mintához – ahogy a statisztikusok mondják, megbecsüljük őket. Ahhoz, hogy az így kapott becslések jó tulajdonságúak legyenek – például a véges méretű mintából becsült paraméterek a valódi értékeik körül ingadozzanak – bizonyos feltevéseknek teljesülniük kell (kezdve természetesen azzal, hogy a változók közti összefüggés valóban ilyen alakú, azaz lineáris legyen), ezeket hívjuk modellfeltevéseknek, az ellenőrzésüket pedig modelldiagnosztikának. Fontos a kapott modell jóságának jellemzése, a modellminősítés is.
Amennyiben az eredményváltozónk nem folytonos, hanem kategoriális (legegyszerűbb esetben: bináris), akkor a fenti eljárás nem követhető. Ilyenkor nem a 0/1 jellegű kimenetet akarjuk közvetlenül modellezni, hanem az 1 kimenet valószínűségét, de még ez sem oldja meg a problémát: gondoljunk bele, a lineáris regresszió adhatna 0-nál kisebb vagy 1-nél nagyobb értéket is. Éppen ezért bár megtartjuk a fenti lineáris struktúrát, de annak eredményét előbb transzformáljuk egy olyan függvénnyel, ami az egész számegyenest a ![]() tartományra képezi le. Így már tekinthető a modell kimenete valószínűségnek; persze a paraméterek becslése – az adatok modellhez való illeszkedésének mérése – bonyolultabb lesz. A legnépszerűbb választás az említett transzformációra az
tartományra képezi le. Így már tekinthető a modell kimenete valószínűségnek; persze a paraméterek becslése – az adatok modellhez való illeszkedésének mérése – bonyolultabb lesz. A legnépszerűbb választás az említett transzformációra az ![]() alakú ún. logisztikus függvény alkalmazása, az ezt használó eljárás neve innen: logisztikus regresszió.
alakú ún. logisztikus függvény alkalmazása, az ezt használó eljárás neve innen: logisztikus regresszió.
A logisztikus regresszió tehát közvetlenül egy valószínűséget ad meg. Ahhoz, hogy bináris besorolást kapjunk, egy küszöböt (cut-off) kell meghatároznunk, ami fölött 1, alatta 0 kategóriába osztályozzuk a megfigyelést. Fontos, hogy ezt a cut-off-ot nem a logisztikus regresszió határozza meg, annál is inkább, mert ez a saját, egyéni preferenciáinkat is kell, hogy tükrözze: ha attól a hibától félünk jobban, hogy egy 1-eset tévesen 0-ba sorolunk, akkor érdemes a cut-off-ot alacsonyra venni, ha inkább az a baj, ha egy 0 tévesen az 1-es kategóriába kerül, akkor viszont magasra. (Nagyon gyakori a kétféle hiba elkerülésére az az – orvosi gyakorlatból átvett – szóhasználat, amikor annak a valószínűségét, hogy egy valójában 1-es alanyt tényleg 1-esnek sorolunk szenzitivitásnak (érzékenység), annak a valószínűségét, hogy egy valójában 0-s alanyt tényleg 0-snak sorolunk specificitásnak (fajlagosság) nevezzük.) A szenzitivitás és a specificitás jól jellemzi a modellt egy adott cut-off mellett, de ha általában vagyunk a jóságára kíváncsi, akkor célszerű megnézni, hogy az összes lehetséges cut-off mellett milyenek az összetartozó szenzivitás/specificitás párok4. Ennek egy tipikus ábrázolása, amikor a különböző cut-off-ok melletti szenzitivitásokat az (1-specificitás) értékekkel szemben ábrázoljuk, ennek neve: ROC-görbe. Ezen a bal alsó és a jobb felső pont felel meg az előbbi lábjegyzetben említett két szélsőséges esetnek, a kettőt összekötő görbén vannak azok a modellek, amelyek pénzfeldobással sorolnak be (különbözőképp cinkelt pénzérmékkel). A tökéletes modell a bal felső pontban van, ennek megfelelően egy konkrét modell jellemzésének gyakori eszköze, hogy mekkora a terület a ROC-görbéje alatt (AUC): a véletlenszerű modelleknél ez ![]() , a tökéletes modellnél 1.
, a tökéletes modellnél 1.
A szerző elsősorban a logisztikus regressziót alkalmazta kérdésének vizsgálatára.
Egész pontosan három részkérdésre bontotta a feladatot, ezek közül is az első annak előrejelzése volt, hogy egy adott buli5 időpontjában elérhető adatok alapján valamely játékos a következő buli időpontjakor a jégen lesz-e. (Ez tehát azt jelenti, hogy minden bulihoz – kivéve a legelsőt – és minden játékoshoz tartozik egy modell!) A magyarázó változókat az jelenti, hogy a korábbi játékmegszakítások időpontjában kik voltak a pályán (minden korábbi játékmegszakításra, és minden játékosra), kiegészítve néhány, szakmailag fontosnak ítélt változóval (például, hogy emberelőnyben volt-e a vizsgált csapat a buli időpontjában, vagy, hogy mennyi idő telt el a legutóbbi buli óta).
Látható, hogy ez rettenetes mennyiségű magyarázó változót jelent, amelyek felhasználása problémás, vagy egyenesen lehetetlen lenne. (Ha több magyarázó változónk van, mint megfigyelésünk, akkor belátható, hogy elvileg sem lehet megbecsülni a paramétereket, de ha több a megfigyelés, ám nem sokkal, akkor is lehet, hogy nagyon bizonytalan lenne a becslés, vagy túl rossz lenne az általánosítóképessége a modellnek – hogy ez utóbbi mit jelent, arra rögtön visszatérünk.) Éppen ezért a szerző változószelekciót alkalmazott: egy – közelebbről meg nem határozott – módszerrel minden magyarázó változóhoz hozzárendelt egy ,,hasznossági értéket'' (hogy mennyire lényeges az adott változó az eredményváltozó leírásában), és csak a legjobb hasznosságú változókat vonta be a modellbe.
Ha ilyen változószelekciót is használ az ember, különösen fontos a modell validálása. Az teszi szükségessé ennek használatát, hogy a szokásos modellminősítés esetén ugyanazokon az adatok találjuk ki (becsüljük meg) a modellt, mint amik alapján lemérjük a jóságát. Ez nyilvánvalóan torzításhoz vezet, hiszen a modell ,,unfair előnyt kap'' azáltal, hogy egy megfigyeléshez tud igazodni is (hiszen felhasználjuk a becsléshez) majd ugyanazon mérjük le azt is, hogy mennyire jól igazodott hozzá! A modell igazi célja nem az, hogy a mintánkat jól leírja (ha csak ezt akarnánk, akkor kár is modellt alkotni, ott a minta), hanem, hogy a mintán kívüli világról, amiből a minta származik – ahogy a statisztikusok mondják: a sokaságról – mondjunk valamit, hogy általánosítani lehessen a modell eredményeit a sokaságra. Nem az a feladat, hogy a mintában lévő eredményváltozókat jól eltaláljuk, hanem, hogy ha jön egy új, mintában nem szereplő megfigyelés, akkor annak eredményváltozóját jól eltaláljuk! Ennek lemérésére tehát a szokványos modellminősítés nem jó, torzított módszer. A szerző éppen ezért kettéosztja a mintáját: az adatok 80%-át az ún. tanítóhalmazba rakja, ezen megfigyelések alapján becsli meg a modellt, ám annak jóságát már a maradék 20%-on, az ún. teszthalmazon méri le! Ilyen módon a modellt tényleg olyan adatok alapján minősíti, amiket az még soha nem látott (tehát nem használódott fel a tanításához).
A szerző egy kiválasztott neves játékosra, Teema Selänne-re vonatkoztatva közli az eredményeit. Eszerint a végleges modelljében, még a tesztadatokon is ![]() értékű az AUC, a használt cut-off mellett az érzékenység 48%. (A specificitás adatait nem közli, de a ROC-görbe alapján 90% körülinek tűnik.)
értékű az AUC, a használt cut-off mellett az érzékenység 48%. (A specificitás adatait nem közli, de a ROC-görbe alapján 90% körülinek tűnik.)
Most, hogy van egy jó modellünk az egyes játékosok pályára lépési valószínűségeinek megtippelésére, a következő lépés annak meghatározása, hogy mi lesz a teljes csapat összeállítása a legközelebbi játékmegszakítás pillanatában. (A dolog azért nem triviális folyománya az előbbinek, mert ez már tekintettel van a csapat összeállítására is, tehát, hogy milyen pozíciók vannak egyáltalán egy jégkorongcsapatban – amiken természetesen nem felcserélhetőek az egyes játékosok.) Ezt a feladatot valósítja meg a második modell. Ehhez felhasználja magyarázó változóként az első modell által predikált valószínűségeket – sőt, más, nem logisztikus regressziós módszerek által szolgáltatott becsült valószínűségeket is –, valamint ezúttal is bevon a szerző néhány szakmai alapon kiválasztott további magyarázó változót.
A helyzet modellezési szempontból annyiban más, mint az első modellnél, hogy nem egyszerűen azt kell megmondani, hogy egy játékos pályára lép-e (binárisan), hanem azt is, hogy melyik pozícióban. Míg az előbbi esetben egy darab valószínűséget kell visszaadnunk, itt most 6-ot (egy jégkorongcsapat 6 játékosból áll). Úgy is fogalmazhatnánk, hogy míg az első esetben 2 lehetséges kategória valamelyikébe kell az alanyokat besorolnunk (pályára lép/nem lép pályára), itt most 7 kategória egyikébe. Ez is osztályozási feladat tehát, csak immár – úgy szokás mondani – többosztályos. Erre létezik a logisztikus regressziónak egy meglehetősen direkt általánosítása6, ezt multinomális logisztikus regressziónak szokás nevezni7.
A szerző ezzel a modellel 40–50% körüli találati arányt tudott elérni (természetesen itt is használva a változószelekciót, és itt is validálva az eredményeket) – innen is látszik, hogy ez a feladat jóval nehezebb, mint pusztán a pályára lépési valószínűség megtippelése.
Ezt követi az utolsó, harmadik modell alkalmazása – ez az, ami az igazán központi kérdésre választ fog adni: hogyan maximalizáljuk ügyes cserével a gólszerzési valószínűséget? A második modellből már tudjuk, hogy mik a legvalószínűbb összeállítású sorok, de egyelőre még semmit nem tudunk a gólszerzési valószínűségekről. A szerző megközelítésének a lényege, hogy veszi a második modellből minden pozícióra a két legvalószínűbb játékost, és belőlük képez ún. ,,alternatív sorokat'' az összes lehetséges kombinációt tekintve (azaz összesen ![]() sort8). Ezután jön a gólszerzési valószínűség bevonása: ezt ismét csak logisztikus regresszióval vizsgálja, ahol az eredményváltozó az, hogy az adott sor lő-e gólt, a magyarázó változókat pedig a korábbi sorösszetételek jelentik, ezúttal is kiegészítve néhány szakmai alapon kézzel kiválasztott változóval. Miután megvannak az ezen modell által megadott gólszerzési valószínűségek, a szerző módszerének utolsó lépését az jelenti, hogy az – előbb definiált – alternatív sorokból kivesszük azt a játékost, amelyre a predikált gólszerzési valószínűség maximális.
sort8). Ezután jön a gólszerzési valószínűség bevonása: ezt ismét csak logisztikus regresszióval vizsgálja, ahol az eredményváltozó az, hogy az adott sor lő-e gólt, a magyarázó változókat pedig a korábbi sorösszetételek jelentik, ezúttal is kiegészítve néhány szakmai alapon kézzel kiválasztott változóval. Miután megvannak az ezen modell által megadott gólszerzési valószínűségek, a szerző módszerének utolsó lépését az jelenti, hogy az – előbb definiált – alternatív sorokból kivesszük azt a játékost, amelyre a predikált gólszerzési valószínűség maximális.
A harmadik lépés modelljében szereplő logisztikus regresszió validált AUC-je ![]() . Az egész procedúrát tekintve elmondható, hogy az eljárás az esetek 74%-ában javasol olyan sort, melynek a predikált gólszerzési valószínűsége nagyobb volt, mint a ténylegesen pályára küldötté. (Persze azt nem tudhatjuk, adat híján, hogy ezek valóban valószínűbben szereztek-e volna gólt.)
. Az egész procedúrát tekintve elmondható, hogy az eljárás az esetek 74%-ában javasol olyan sort, melynek a predikált gólszerzési valószínűsége nagyobb volt, mint a ténylegesen pályára küldötté. (Persze azt nem tudhatjuk, adat híján, hogy ezek valóban valószínűbben szereztek-e volna gólt.)
Az olvasó észrevételei
Természetesen egyetlen recenzió sem lehet teljes anélkül, hogy néhány kritikus észrevétel, továbbfejlesztési lehetőséget meg ne fogalmaznánk:
- Mindhárom modell esetében jobb eredményt produkál a modell a tesztadatokon, mint a tanítómintán. Ez, ha nem is elvileg, de gyakorlatilag lehetetlen. Itt valami biztos nem stimmel, jobb esetben az oszlopfeliratok, rosszabb esetben az eredmények keveredtek össze!
- Furcsa, hogy az első modellben fix
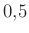 volt a cut-off. Miért? Miért nem optimalizálta a szerző ezt az értéket...? Annál is inkább, mert közölte a teljes ROC-görbét, ami alapján ez könnyedén megtehető lett volna. (Ráaadásul még csak fel sem tüntette a
volt a cut-off. Miért? Miért nem optimalizálta a szerző ezt az értéket...? Annál is inkább, mert közölte a teljes ROC-görbét, ami alapján ez könnyedén megtehető lett volna. (Ráaadásul még csak fel sem tüntette a 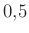 helyét a ROC-görbén, így azt sem látjuk közvetlenül, hogy a szerző modellje hol volt.) Hasonlóan nem derül ki, hogy a harmadik modellnél miért épp a
helyét a ROC-görbén, így azt sem látjuk közvetlenül, hogy a szerző modellje hol volt.) Hasonlóan nem derül ki, hogy a harmadik modellnél miért épp a 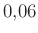 -ot választotta ki...
-ot választotta ki... - A pontosság használatának az első modell esetében nem sok teteje van, hiszen ha egy játékos sokat volt a pályán (a példaként hozott Teema Selänne a tanító adatok alapján az esetek
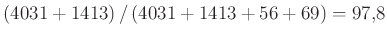 %-ában pályán volt!), akkor az a modell is remek pontosságú, ami magyarázó változóktól függetlenül mindig azt predikálja, hogy a pályán lesz! (Jobb lett volna a 2. táblázatban inkább a specificitást is számszerűen megadni.)
%-ában pályán volt!), akkor az a modell is remek pontosságú, ami magyarázó változóktól függetlenül mindig azt predikálja, hogy a pályán lesz! (Jobb lett volna a 2. táblázatban inkább a specificitást is számszerűen megadni.) - Érdekes lett volna tudni, hogy pontosan milyen jellemzőkiválasztási módszert használt a szerző.
Ezekkel együtt is a modell alapfeltevése kifejezzen érdekes, a használt módszerek megfelelnek a ,,korszerű'' sport-statisztika megközelítésének, így csak remélni lehet, hogy a további fejlesztések révén gyakorlatban is alkalmazható eszközt nyer a szerző.
Ferenci Tamás
Élettani Szabályozások Csoport, Óbudai Egyetem
Irodalomjegyzék
- 1
- Three perspectives of data mining. Artificial Intelligence, 143(1):139–146, 2003.
- 2
- Abonyi János: Adatbányászat – a hatékonyság eszköze. Computerbooks, 2006.
- 3
- Bodon Ferenc: Adatbányászati algoritmusok.
- http://www.cs.bme.hu/~bodon/magyar/adatbanyaszat/tanulmany/adatbanyaszat.pdf, 2010.
- 4
- Leo Breiman et al. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Statistical Science, 16(3):199–231, 2001.
- 5
- Jerome H Friedman. Data mining and statistics: What's the connection? Computing Science and Statistics, 29(1):3–9, 1998.
- 6
- Jiawei Han és Micheline Kamber. Adatbányászat – Koncepciók és technikák. Panem, 2004.
- 7
- David J. Hand. Data mining: Statistics and more? The American Statistician, 52(2):112–118, 1998.
- 8
- F. Harrell. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis. Springer Series in Statistics. Springer International Publishing, 2015.
- 9
- T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Series in Statistics. Springer New York, 2013.
- 10
- P. Langley. Elements of Machine Learning. Machine Learning Series. Morgan Kaufmann, 1996.
- 11
- M. Marchi and J. Albert. Analyzing Baseball Data with R. Chapman & Hall/CRC The R Series. CRC Press, 2016.
- 12
- Bolla Marianna és Krámli András: Statisztikai következtetések elmélete. Typotex, 2005.
- 13
- Móri Tamás és Székely Gábor: Többváltozós statisztikai analízis. Műszaki Könyvkiadó, 1987.
- 14
- K. P. Murphy. Machine Learning: A Probabilistic Perspective. Adaptive computation and machine learning series. MIT Press, 2012.
- 15
- Lori Ploutz-Snyder et al. Age, body mass, and gender as predictors of masters olympic weightlifting performance. Medicine and science in sports and exercise, 35(7):1216–1224, 2003.
- 16
- Brian Ripley. Data mining: Large databases and methods or..., 5 2004. Keynote speech at UseR! 2004 [Accessed: 24/08/2016].
- 17
- Nenad Rogulj, Vatromir Srhoj, and Ljerka Srhoj. The contribution of collective attack tactics in differentiating handball score efficiency. Collegium antropologicum, 28(2):739–746, 2004.
- 18
- Stuart Russel és Peter Norvig: Mesterséges intelligencia modern megközelítésben. Panem, 2005.
- 19
- A Santos-Lozano, PS Collado, C Foster, A Lucia, and N Garatachea. Influence of sex and level on Marathon pacing strategy. insights from the New York city race. International journal of sports medicine, 35(11):933–938, 2014.
- 20
- Südy Barbara: Jégkorongcsapat összeállításának valós idejű optimalizálása adatbányászati eszközök segítségével.
Alkalmazott Matematikai Lapok, 32:41–61, 2015. - 21
- P. N. Tan, M. Steinbach, and V. Kumar. Introduction to Data Mining. Addison-Wesley, 2013.
Lábjegyzetek
- 1
- Brian Ripley, az alkalmazott statisztika egyik jól ismert kortárs alakja, a Modern Applied Statistics with S (MASS) című alapkönyv szerzője egyszer úgy fogalmazott: ,,A gépi tanulás nem más mint statisztika, mínusz a modellfeltevések teljesülésének bármiféle ellenőrzése!'' [16].
- 2
- Bár a széles nagyközönség számára ez is újdonság lehet; emlékezetes, hogy mekkora híre ment, amikor a 2006-os labdarúgó világbajnokság negyeddöntőjében Jens Lehman, a német válogatott kapusa az argentinok elleni tizenegyespárbaj során a sportszárába rejtett fecniről olvasta le, hogy a soron következő lövőnek a múltbeli adatok alapján mi a legkedveltebb választása a lövés helyezését illetően.
- 3
- Ezért a lineáris regresszió az ún. paraméteres regressziók nagyobb csoportjába tartozik, ahol a függvényforma adott, és csak néhány paraméter megbecslése a feladat. Természetesen ezek eredményei alapján módosítható a függvényforma is.
- 4
- Az előbbiből már következik, hogy 0 cut-off esetén – mindenkit 1-be sorolunk – a modell tökéletesen szenzitív, de nulla a specificitása, 1 cut-off mellett – mindenkit 0-ba sorolunk – a modell tökéletesen specifikus, de nulla a szenzitivitása.
- 5
- Korongbedobást maga után vonó játékmegszakítás a hokiban.
- 6
- Lényegében arról van szó, hogy kiválasztjuk az egyik kategóriát, és az összes többi kategóriára gyártunk egy szokásos – kétosztályos – logisztikus regressziót, melyben az adott kategória és a kiválasztott kategória között osztályozunk.
- 7
- A szerző – a recezens véleménye szerint igen ritkán használt, és nem is túl szerencsés módon – ezt polinomiális logisztikus regressziónak nevezi.
- 8
- Bár a cikkből nem derül ki, de sejthetőleg a kapust rögzítetten tartja a szerző.