Milyenek az optimális befektetések … és hogyan találjuk meg őket?

A közgazdaságtan matematikai elméletében szokásos a befektetők pénzhez való viszonyát ún. hasznossági függvényekkel jellemezni. Egy ilyen $U\colon (0,\infty)\to\mathbb{R}$ függvény $U(x)$ értéke azt fejezi, ki hogy az adott befektető mennyire elégedett $x\in (0,\infty)$ forinttal, mennyi hasznot jelent számára ez az összeg, szubjektív értelemben.

Az $U$ függvény jellemző tulajdonságai vita tárgyát képezik. Abban talán mindenki egyetért, hogy $U$ folytonos (hiszen kis változás a vagyoni helyzetben csak kis mértékben változtatja meg az elégedettség szintjét), és monoton növő (több pénznek jobban örülünk). Mi mostantól feltesszük, hogy $U$ szigorúan monoton növő és folytonosan differenciálható.

Még egy fontos jellemző tulajdonság lehet, hogy $U$ konkáv, ez a feltevés azonban már vitatható, amint azt alább részletesebben kifejtjük. Már Daniel Bernoulli úttörő [1] cikkében is konkáv $U$ szerepelt. Ezt a tulajdonságot a befektetők kockázatkerülő magatartásával szokás magyarázni: egy kis $\Delta>0$ csökkenés a vagyonban $U(x)-U(x-\Delta)\approx \Delta U'(x)$ -szel csökkenti a hasznosságot. Ha $U$ konkáv, akkor $x$ csökkenésével ez a mennyiség egyre nő, azaz az elégedettség egyre gyorsuló ütemben csökken. Különösen igaz ez a 0 (= csőd) közelében, ezért általában olyan $U$ -t használnak, melyre $U'(x)\to\infty$ , $x\to 0$ , például $U(x)=\gamma x^{\gamma}$ valamely $\gamma<1$ , $\gamma\neq 0$ számra, vagy $U(x)=\ln(x)$ .

Egyelőre tegyük fel, hogy $U$ konkáv (a későbbiekben majd tárgyalunk egyéb eseteket is). Nézzük meg, hogyan tűzhető ki az optimális befektetési feladat az adott hasznossági függvénnyel bíró piaci szereplő számára!

A lehetséges portfólió stratégiák halmazát célszerű egy $\Phi$ vektortérrel leírni (mely általában végtelen dimenziós és valamely topológiával is el van látva). A vektortér struktúra annak felel meg, hogy ha $\phi_1,\phi_2\in\Phi$ portfóliók kereskedhetők, akkor általában azok egyesítése $\phi_1+\phi_2$ is, valamint valós konstansszorosa is, tehát $\alpha\phi_1$ minden $\alpha\in\mathbb{R}$ -re. Negatív $\alpha$ azt jelenti, hogy az adott portfóliót nem vesszük, hanem eladjuk, erre sok piacon van lehetőség. A $\phi\in\Phi$ portfólió ára $p(\phi)$ , kézenfekvő feltenni, hogy $p(\cdot)$ lineáris függvény. Az adott $\phi$ portfólió hozama a $Z(\phi)$ valószínűségi változó (hiszen a legtöbb befektetés bizonytalan kimenetelű). A $\phi\to Z(\phi)$ hozzárendelés is lineáris. Ha a befektetőnek $c>0$ kezdeti tőkéje van, akkor olyan portfóliók közül választhat, melyekre $p(\phi)\leq c$ teljesül. Ha a $\phi$ befektetés mellett dönt, akkor vagyona $c$ -ről $c-p(\phi)+Z(\phi)$ -re változik.

Csak azokat a befektetéseket engedjük meg, melyek a csődöt elkerülik, ezért a megengedett portfóliók halmaza

$\displaystyle \mathcal{A}(c):=\{\phi\in\Phi\colon p(\phi)\leq c,\ c-p(\phi)+Z(\phi)\geq 0\}.$

Ez $\Phi$ -nek konvex részhalmaza.

Az adott piaci szereplő célja, hogy ezek közül kiválassza a számára legmegfelelőbbet. Az optimális befektetési feladat tehát így fogalmazható meg: keressük azt a $\phi^*=\phi^*(c)\in\mathcal{A}(c)$ befektetést, melyre

$\displaystyle u(c):=\sup_{\phi\in\mathcal{A}(c)}E[U(c-p(\phi)+Z(\phi))]=E[U(c-p(\phi^*)+Z(\phi^*))],$

(1)

azaz $E$ -vel jelölve a várható érték operátort, a várható hasznosság a $\phi^*$ stratégiát követve lesz a legnagyobb. Itt valójában feladatok egy családjáról beszélhetünk, amit a $c>0$ paraméterez.

A feladat helyesen kitűzött, ha $u(c)<\infty$ minden $c>0$ -ra. Láthatóan konkáv funkcionálokat kell maximalizálni egy (topologikus) vektortér valamely konvex részhalmazán. Mivel $\Phi$ többnyire végtelen dimenziós, az ilyen $\phi^*$ létezésének bizonyítása nem egyszerű feladat, még konkrét modellek esetében sem.

A probléma abban rejlik, hogy ha pl. $\Phi$ egy Banach-tér, $\mathcal{A}(c)$ pedig annak korlátos részhalmaza (általában még csak nem is korlátos!), akkor sem kompakt a normatopológiában. Tehát, ha $\phi_n\in\mathcal{A}(c)$ egy sorozat, melynek mentén az (1)-ben szereplő a szuprémum eléretik, akkor nem feltétlenül lehet belőle konvergens részsorozatot kiválasztani!

Természetesen léteznek ügyes technikák a nehézségek leküzdésére. Példaképpen az alábbi fontos tételt idézzük.

Tétel. (Komlós János, [4]) Ha $(\Omega,\mathcal{F},P)$ egy valószínűségi mező, $f_n$ , $n\in\mathbb{N}$ pedig valószínűségi változók olyan sorozata, amelyre $\sup_n E[f_n]<\infty$ , akkor van olyan $n_k$ , $k\in\mathbb{N}$ részsorozat és egy $f$ valószínűségi változó, amelyre

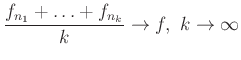
$\displaystyle \frac{f_{n_1}+\ldots+f_{n_k}}{k}\to f,\ k\to\infty$

fenáll a $P$ -majdnem mindenütt konvergencia értelmében.

Azaz kiválasztható majdnem mindenütt értelemben Césaro-konvergens részsorozat. Ehhez hasonló eredmények számos topologikus vektortérben ismeretesek: egy megfelelő értelemben korlátos sorozatnak vannak olyan konvex lineáris kombinációi (a fenti tételben átlagai), amelyek konvergálnak.

Ha tehát a fentebb említett $\phi_n$ sorozat alkalmas értelemben korlátos (ez rendszerint következik abból, hogy aszimptotikusan optimális stratégiákat tekintünk), akkor valamely

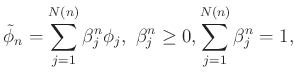
$\displaystyle \tilde{\phi}_n=\sum_{j=1}^{N(n)} \beta_j^n \phi_j,\ \beta_j^n\geq 0,\sum_{j=1}^{N(n)}\beta^n_j=1,$

konvex lineáris kombinációi konvergálnak valamely $\phi^*\in\mathcal{A}(c)$ stratégiához (egy alkalmas topológiában), itt $N(n)$ a konvex kombinációk tagszáma, $\beta^n_j$ pedig a konvex súlyok. (Ehhez persze kell az is, hogy $\mathcal{A}(c)$ zárt legyen a tekintett topológiában.)

Mivel $U$ konkáv, $p(\cdot)$ , $Z(\cdot)$ lineárisak,

$\displaystyle E[U(c-p(\tilde{\phi}^n)+Z(\tilde{\phi}^n))]\geq \sum_{j=1}\beta^n_j E[U(c-p(\phi_n)+Z(\phi_n))],$

(2)

ezért a $\tilde{\phi}^n$ stratégiák várható hasznossága továbbra is az (1)-beli-beli szuprémumhoz tart. Ezek után remélhető (de messze nem nyilvánvaló), hogy a $\phi^*$ stratégia eléri a szuprémumot, tehát optimális lesz.

Az imént vázolt gondolatmenet közvetlenül általában nehezen alkalmazható a pénzügyi matematika modelljeiben. Segít azonban a lineáris programozásban is használatos duális probléma bevezetése. A jelen esetben ez a következő problémacsaládhoz vezet: minden $h>0$ -ra keressük azt az $M^*=M^*(h)\in\mathcal{M}$ -et, amelyre

$\displaystyle v(h):=\inf_{M\in\mathcal{M}}E[V(hM)]=E[V(hM^*)]$

teljesül. Itt $V(y):=\sup_{x>0}[U(x)-xy]$ , $y>0$ az $U$ Fenchel-Legendre konjugáltja, $\mathcal{M}$ pedig (nagyjából) a $Z({\Phi})$ anullátora, vagyis

$\displaystyle \mathcal{M}:=\{\psi\in\Psi^*\colon \psi(Z(\phi))=0,\ \phi\in\Phi\},$

ahol $\Psi^*$ egy olyan $\Psi$ topologikus vektortér duális tere, mely tartalmazza a $\{Z(\phi),\phi\in\Phi\}$ halmazt.

A fenti elvont leírást talán jobban megvilágítja egy konkrét példa. Ha például egy részvénnyel kereskedünk, akkor $\mathcal{M}$ (nagyjából) azonosítható azon $Q\sim P$ valószínűségi mértékek halmazával, melyekre nézve a részvényárfolyamat martingál.

Általában viszonylag könnyű igazolni, hogy a duális problémának van megoldása, amiből (1) megoldása egy explicit transzformációval megkapható (persze mindez a modelltől függő, cseppet sem egyszerű meggondolásokat igényel). Igazolható az is, hogy a $v$ függvény az $u$ Fenchel-Legendre konjugáltja, illetve a primál/duál problémák közötti szokásos összefüggések is bizonyíthatók.

A duális problémán alapuló megoldási módszer először [5]-ben lett részletesen kidolgozva. Ez az elegáns és hatékony megközelítés azonban nem mindig működik. Például ha bizonytalan a $P$ mérték, csak annyit tudunk róla hogy valószínűségi mértékek egy $\mathcal{P}$ családjába esik, akkor modellbizonytalanság áll fenn, és célszerű (1) helyett inkább az

$\displaystyle u(c):=\sup_{\phi\in\mathcal{A}(c)}\inf_{P\in\mathcal{P}}E_P[U(c-p(\phi)+Z(\phi))],$

(3)

problémát tekinteni. Ez jóval nehezebb, és ismert, hogy duális problémájának nincsen mindig megoldása. Ilyen és hasonló okok rákényszerítenek arra, hogy (3) megoldását közvetlenül, a duális problémát mellőzve találjuk meg.

Ilyen eredmények először [7]-ben bukkantak fel $(0,\infty)$ -en definiált $U$ -ra. Nagyon fontos azonban $U\colon \mathbb{R}\to \mathbb{R}$ hasznossági függvényeket is vizsgálni, ezekkel elemezhető a veszteségek hatása is: $x<0$ esetén $U(x)$ a befektető „csalódottságának” mértéke. Az ilyen $U$ -k használatán számos kockázetelemzési módszer alapul. Ilyenkor az (1) feladat nehezebb (és persze a stratégiák $\mathcal{A}(c)$ osztályát is módosítani kell). Közvetlen, a duális problémát elkerülő megközelítést sikerült adnunk [6]-ben, mely a fenti Komlós tétel egy új, [2]-ból származó változatán alapszik. A felhasznált topologikus vektorterek az ún. Orlicz-terek, melyek a funkcionálanalízisből jól ismert $L^p$ terek általánosításai.

A [3] cikk szerzői kísérletekkel támasztották alá, hogy a befektetők $U$ hasznossági függvénye ún. „S-alakú”: valamely $b>0$ -ra konvex a $(0,b)$ és konkáv a $(b,\infty)$ intervallumokon. (Ezért 2002-ben Kahnemann közgazdaságtani Nobel-díjat kapott.) Ilyenkor a duális probléma értelmét veszti, és a Komlós tétel változatai sem használhatóak (mert (2) nem igaz). Ilyen esetekben teljesen más módszerek szükségesek és csak kevés eredmény ismeretes.

A téma iránt mélyebben érdeklődőknek a [8] könyv 7. fejezete ajánlható (a megfelelő előismeretek elsajátítása után), illetve a [7] jegyzet is jól olvasható.

Rásonyi Miklós

MTA Rényi Alfréd Matematikai Kutatóintézet

Irodalomjegyzék

[1] D. Bernoulli. Exposition of a new theory on the measurement of risk. Econometrica, 22:23—36, 1954. (Az 1738-ban megjelent latin eredeti angol fordítása.)

[2] F. Delbaen, K. Owari. Convex functions on dual Orlicz spaces. arXiv:1611.06218

[3] D. Kahnemann, A. Tversky. Prospect theory: An analysis of decision under risk. Econometrica, 47:263—291, 1979.

[4] J. Komlós. A generalization of a problem of Steinhaus. Acta Mathematica, 18:217—229, 1967.

[5] D. Kramkov, W. Schachermayer. The condition on the Asymptotic Elasticity of Utility Functions and Optimal Investment in Incomplete Markets. Annals of Applied Probability, 9:904—950, 1999.

[6] M. Rásonyi. On optimal investment without passing by the dual problem. arXiv:1702.00982

[7] W. Schachermayer. Portfolio Optimization in Incomplete Financial Markets. Notes of the Scuola Normale Superiore Cattedra Galileiana, Pisa, 2004. Letölthető a http://www.mat.univie.ac.at/~schachermayer/pubs/index.php honlapról a [116]-os publikáció.

[8] H. Pham. Continuous-time Stochastic Control and Optimization with Financial Applications, Springer, 2009.

Fotó: https://www.pexels.com/photo/u-s-dollar-bills-pin-down-on-the-ground-164474/