Rácz András barátom, az alapos lektorok kihalóban lévő fajtájának képviselője azzal a kérdéssel fordult hozzám, hogy a 2015-ös Putnam-verseny egyik feladatának számítógéppel segített megoldásában megakadt, tudnék-e neki segíteni. A Putnam-verseny sokkal több egyetemista számára elérhető, mint a mi Schweitzer Miklós Emlékversenyünk. (Ez utóbbin egy időben sikerült a lécet oly magasra tenni, hogy a versennyel foglalkozó akadémikusok száma meghaladta a versenyezni bátor egyetemisták számát. De hogy tájékoztassuk a tájékozatlanokat: ezen a versenyen 10 feladat szokott szerepelni, megoldásukra van 10 nap, ezalatt bármilyen eszköz használható, számítógép és könyvek is. Ez utóbbiaknál kívánatos, hogy a könyvtárból senki ne vegye ki azt a könyvet, amelyik esetleg releváns információt tartalmaz valamely feladatra vonatkozóan. Természetesen egymással sem illik(!) kommunikálni, eltekintve az olyan üzenetektől, hogy „Nekem már három megvan!”. Tanárnál nem érdemes kérdezősködni, mert köztük nem sok van, aki néhánynál több feladatban tudna segíteni... A versenyzők etikájára jellemző, hogy egy alkalommal egyikük erősen követelte a javítóktól, hogy vegyék észre, az ő megoldása nem helyes, és emiatt vonjanak le a pontszámából, és helyezzék hátrébb. Az illető ma már Nagy Britannia közoktatását erősíti.)
A szóban forgó feladat tehát a következő:
Legyen ![]() , és ha
, és ha ![]() , akkor
, akkor ![]() . Keressük meg
. Keressük meg ![]() egy páratlan prímtényezőjét.
egy páratlan prímtényezőjét.
Mivel az ![]() sorozat egy másodrendű lineáris, állandó együtthatós differenciaegyenletnek tesz eleget, ezért a kezdeti feltételeket is kielégítő megoldását a szokásos módon (l. pl. [1, 58–59. oldal]) kaphatjuk meg: meghatározzuk a
sorozat egy másodrendű lineáris, állandó együtthatós differenciaegyenletnek tesz eleget, ezért a kezdeti feltételeket is kielégítő megoldását a szokásos módon (l. pl. [1, 58–59. oldal]) kaphatjuk meg: meghatározzuk a ![]() karakterisztikus egyenlet gyökeit; ezek
karakterisztikus egyenlet gyökeit; ezek ![]() . Így az általános megoldás
. Így az általános megoldás ![]() , az együtthatókat pedig a kezdeti feltételekből kiszámolva végül ezt kapjuk:
, az együtthatókat pedig a kezdeti feltételekből kiszámolva végül ezt kapjuk: 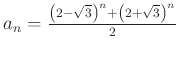 . Ezt a számolást a Mathematica is hajlandó elvégezni helyettünk, ha így kérjük tőle:
. Ezt a számolást a Mathematica is hajlandó elvégezni helyettünk, ha így kérjük tőle:
Egyelőre sokkal nem jutottunk előbbre, pedig explicit képletünk van a sorozat tagjaira, amelyek mellesleg pozitív egész számok, de ez nem kiabál az explicit képletről. Minden konkrét ![]() esetére azonban kifejthetjük a hatványokat, és máris ott áll előttünk egy 1153 jegyű szám.
esetére azonban kifejthetjük a hatványokat, és máris ott áll előttünk egy 1153 jegyű szám. ![]() . (Megkíméljük az olvasót a számjegyek közlésétől.) Ha elosztjuk ezt a számot 2 egymás utáni hatványaival, akkor kiderül, hogy 4 osztója, de 8 már nem. Egy páratlan osztója tehát
. (Megkíméljük az olvasót a számjegyek közlésétől.) Ha elosztjuk ezt a számot 2 egymás utáni hatványaival, akkor kiderül, hogy 4 osztója, de 8 már nem. Egy páratlan osztója tehát ![]() . De az nem prím, mert
. De az nem prím, mert ![]() eredménye False. A hiszékenyebbek elfogadják ezt a választ, de legyünk óvatosak, mert a program úgynevezett valószínűségi algoritmust használ, amely csak annyit garantál, hogy az eredmény nagy valószínűséggel helyes. Aki biztosra akar menni, az használja inkább a ProvablePrimeQ függvényt. Esetünkben ez is False eredményt ad.
eredménye False. A hiszékenyebbek elfogadják ezt a választ, de legyünk óvatosak, mert a program úgynevezett valószínűségi algoritmust használ, amely csak annyit garantál, hogy az eredmény nagy valószínűséggel helyes. Aki biztosra akar menni, az használja inkább a ProvablePrimeQ függvényt. Esetünkben ez is False eredményt ad.
A FactorInteger függvény tetszőleges egész szám prímtényezős előállítását adja meg. Ezen a még mindig nagy számon viszont kivárhatatlanul sokáig futna. De megkereshetjük az előállítás két tényezőjét is, így: ![]() . Kisebbik eredményül a
. Kisebbik eredményül a ![]() számot kapjuk, és ennek teljes prímtényezős felbontása:
számot kapjuk, és ennek teljes prímtényezős felbontása: ![]() , tehát mindjárt két páratlan prímosztót is kaptunk.
, tehát mindjárt két páratlan prímosztót is kaptunk.
Eddig megvolnánk. De ez az a pont, ahol meg kellett kérdeznem Pelikán Józsefet, aki saját jogán négyszeres matematikai diákolimpikon, emellett megszámlálhatatlanul (bár véges) sok diákolimpikon felkészítője évtizedek óta. Érdeklődő levelemre a következő választ kaptam:
„Élvezet nézni, ahogy a Mathematica elbánik az ilyen típusú problémákkal. Ezzel együtt versenyen ez nem számítana megoldásnak. A probléma a gyakorlatban szerencsére fel sem merül, mert valamennyi általam ismert (magyar vagy nemzetközi) zárthelyi versenyen tilos nemcsak számítógépek, hanem kis kézi számológépek (továbbá mobiltelefonok) használata is. Ezenkívül könyveket és jegyzeteket (saját kézzel írottakat is) tilos használni. A Kürschák-versenyen még néhány éve könyv és jegyzet engedélyezett volt, most már ott is tilos. Marad a körző és vonalzó...
Hosszabb távú (pl. Schweitzer) versenyeken nyilván ki sem tűznének ilyen feladatokat, hiszen nem akadályozható meg Mathematica, Maple, stb. használata. El tudom képzelni, hogy a Putnam-szervezők is haboztak kissé. De végül is elég meggyőző az elegáns matematikai megoldás...”
Ezt már nem idézem a levélből, hogy maradjon lehetősége gondolkodnia annak, aki akar. Ha megvan a megoldás, megnézhetjük, hogy azonos-e a miénk ezzel.
De a végére még maradt két halk megjegyzésem. Egyrészt arról, hogy mennyire ismeri egy rendes matematikus a matematikai programcsomagoknak akár a létét, nemhogy a teljesítőképességét. (Figyelembe véve, hogy a gépektől való idegenkedés még azt is jelentheti, hogy valaki a cikkeit nem saját maga gépeli...) A másik konstruktívabb: igenis, kellene olyan versenyeket is rendezni, ahol lényegesen kihasználható valamely programcsomag matematikai feladat megoldásához.
A feladat leírása Wolfram nyelven itt, a számolásokat tartalmazó Wolfram-nyelvű jegyzetfüzet tartalma pedig itt található.
TJ
Irodalomjegyzék
- 1
- Máté L.: Rekurzív sorozatok, Tankönyvkiadó, Budapest, 1980.