Napjainkban az egyetemen továbbtanuló diákok jelentős része középszintű érettségit tesz matematikából. Az egyetemek nem követelik meg az emelt szintű érettségit, így a diákok többsége nem választja ezt a rögös utat. A sikeres egyetemi tanulmányokhoz viszont egy jeles középszintű érettségi gyakran nem elegendő. A jó hír az, hogy nem minden szakon elengedhetetlen a teljes emelt szintű tananyag ismerete.
Sok éves középiskolai és egyetemi tanítási tapasztalatom alapján megkerestem a középiskolai matematika tananyagban azokat a területeket, amelyeket sokkal jobban kellene tudni a sikeres egyetemi tanulmányokhoz. Alapvetően fontos, hogy a diákok hibátlanul és gyorsan bánjanak a hatványokkal és az algebrai törtekkel, ismerjék az elemi függvények alapvető tulajdonságait és grafikonjait (lásd függvénytábla), jártasak legyenek a függvény-transzformáció területén.
Jelen írásomban a matematika három olyan alapvető területét választottam ki, amivel szinte minden diák találkozik az egyetemen az első féléves matematika kurzusokon. Ezek a határértékszámítás, a differenciálszámítás és az integrálszámítás. Mindegyik témához mutatok néhány alapvető és jellemző feladatot. A feladatok megoldását elkezdem és addig folytatom, amíg az a középszintű érettségi tananyagának ismeretében lehetséges. Az a célom, hogy megmutassam, hogy a megoldás lépéseinek jelentős része sikeresen megtehető akkor is, ha korábban nem hallottunk sem határértékszámításról, sem differenciálszámításról, sem integrálszámításról. Azt állítom, hogy akár 50% fölötti eredményt is elérhetünk egy egyetemi zárthelyi dolgozatban ezen témakörökből, ha algebrából és a függvényekből nagyon biztos alapunk van. Bizonyos szavakat és fogalmakat írásomban félkövérrel kiemeltem, ezzel kívántam jól láthatóvá tenni, hogy milyen típusú egyetemi feladatok megoldásához milyen konkrét középiskolai matematikai ismereteket használunk.
Írásomnak az a célja, hogy arra buzdítsam kollégáimat és az egyetemre készülő diákokat, hogy ezeket a témaköröket kiemelten kezeljék. Ha a diákok úgy érzik, további gyakorlásra van szükségük a középszintű érettségin túl, akkor tegyék meg. Ne az egyetemen, az első kudarcok után szembesüljenek azzal, hogy a középiskolai hiányosságaik akadályozzák meg őket az egyetemi tananyag sikeres teljesítésében.
Határértékszámítás
A határértékszámítás az egyetemen tanított matematikai témakörök közül az egyik, amely a diákoknak a magukkal hozott hiányosságok miatt gondot szokott okozni. Nézzük a következő feladatot:
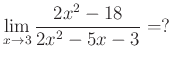
A megoldás menete:
- Kiszámoljuk a számláló és a nevező helyettesítési értékét
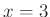 esetén. Mivel mindkettő nulla, ezért
esetén. Mivel mindkettő nulla, ezért - szorzattá alakítjuk a számlálót. Könnyebbé teszi a probléma megoldását, ha tudjuk, hogy a szorzattá alakítást kiemeléssel érdemes kezdeni. Utána nevezetes azonosság alkalmazásával folytatjuk:
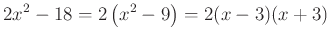
-
A nevezőt is szorzattá kell alakítanunk. Mivel itt nem érdemes kiemelni és nem is nevezetes azonosság, a gyöktényezős alakra hozást alkalmazzuk, ami minden szorzattá alakítható másodfokú kifejezés esetén elvégezhető:
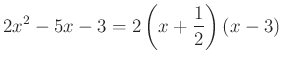
- Egyszerűsítjük a kapott törtet. Éppen azért alakítottuk szorzattá a számlálót és a nevezőt is, hogy ezt megtehessük:
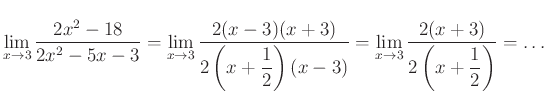
Egészen eddig a lépésig nem kellett figyelembe venni a ![]() jelet, egy algebrai törtön végeztünk azonos átalakításokat. Vegyük észre, hogy a megoldáshoz szükséges öt lépés közül az első négy csak a középiskolai anyag ismeretét igényli.
jelet, egy algebrai törtön végeztünk azonos átalakításokat. Vegyük észre, hogy a megoldáshoz szükséges öt lépés közül az első négy csak a középiskolai anyag ismeretét igényli.
Második feladat:
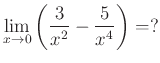
- Mivel a nullával való osztás értelmetlen (és határértékben végtelen lenne), ezért elvégezzük a törtek kivonását. Ehhez először a két nevező legkisebb közös többszörösét keressük meg. Nem érdemes a nevezők szorzatát venni, mert akkor később kénytelenek lennénk egyszerűsíteni, ami megtehető, de fölöslegesen bonyolítaná a feladat megoldását.
- Mivel a két nevező legkisebb közös többszöröse
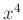 , ezért az első törtet
, ezért az első törtet 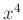 nevezőjűvé bővítjük.
nevezőjűvé bővítjük. - A két azonos nevezőjű törtet kivonjuk egymásból:
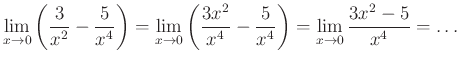
Egészen eddig a lépésig nem kellett figyelembe venni a ![]() jelet, algebrai törtekkel végeztünk azonos átalakításokat. Vegyük észre, hogy a megoldáshoz szükséges négy lépés közül az első három csak a középiskolai anyag ismeretét igényli.
jelet, algebrai törtekkel végeztünk azonos átalakításokat. Vegyük észre, hogy a megoldáshoz szükséges négy lépés közül az első három csak a középiskolai anyag ismeretét igényli.
Differenciálszámítás
Az egyetemen tanított matematika anyag egyik központi kérdése, hogyan lehet egy függvény helyi szélsőértékét (minimumát/maximumát) megkeresni és monotonitási (növekedési/csökkenési) intervallumait meghatározni. Ehhez először deriválni kell a vizsgált függvényt, majd meg kell keresni a deriváltfüggvény zérushelyét. Más szóval olyan egyenletet kell megoldani, ahol az egyik oldalon nulla áll. Majd a deriváltfüggvény előjelét kell meghatározni a teljes értelmezési tartományon.
Feladat: Legyen 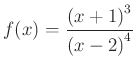 . Határozzuk meg az összes helyi szélsőértékét!
. Határozzuk meg az összes helyi szélsőértékét!
- Először deriváljuk a függvényt:
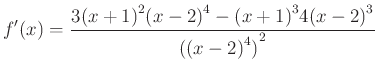
- A számlálóban kiemeljük az összes közös tényezőt az előforduló legnagyobb kitevőn:
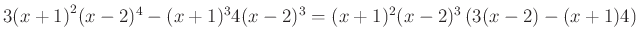
- A nevezőben a hatvány hatványa azonosságot alkalmazzuk:
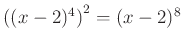
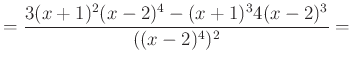 |
|
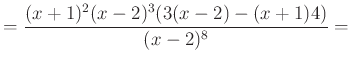 |
|
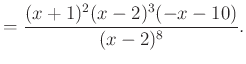 |
- Meg kell oldanunk a
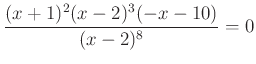 egyenletet.
egyenletet.
a) A törtes egyenleteknél használt módszert alkalmazzuk, beszorzunk a nevezővel majd azt a tételt használjuk, hogy egy szorzat pontosan akkor nulla, ha valamelyik tényezője nulla. Így a
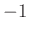 , 2 és 10 értékeket kapjuk. Ezek közül a 2 hamis gyök, ott a nevező is nulla lenne, a 2 nem eleme az eredeti függvény értelmezési tartományának.
, 2 és 10 értékeket kapjuk. Ezek közül a 2 hamis gyök, ott a nevező is nulla lenne, a 2 nem eleme az eredeti függvény értelmezési tartományának.Vagy azt mondjuk, hogy egy tört pontosan akkor nulla, ha a számlálója nulla és a nevezője nem nulla.
b) Egyszerűsítjük a törtet
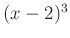 tényezővel, majd megoldjuk a
tényezővel, majd megoldjuk a 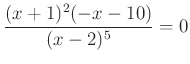 egyenletet az előzőhöz hasonlóan. Így elkerüljük a hamis gyököt, csak a
egyenletet az előzőhöz hasonlóan. Így elkerüljük a hamis gyököt, csak a 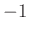 és a
és a 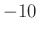 értékeket kapjuk meg.
értékeket kapjuk meg. -
A továbbiakban az egyszerűsített törttel érdemes folytatni a feladat megoldását. Ennek az előjelét kell meghatározni a teljes értelmezési tartományán:
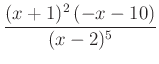
-
Meghatározzuk a számláló előjelét. Egy szorzat előjelét a tényezőinek előjele szabja meg. Mivel
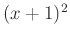 teljes négyzet, ezért az
teljes négyzet, ezért az 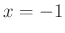 kivételével mindenütt pozitív. A
kivételével mindenütt pozitív. A 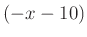 elsőfokú kifejezés, ami
elsőfokú kifejezés, ami 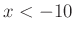 esetén pozitív, különben negatív.
esetén pozitív, különben negatív. - Meghatározzuk a nevező előjelét. Mivel
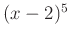 az
az 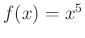 függvény transzformáltja, ezért, ha
függvény transzformáltja, ezért, ha 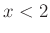 , akkor negatív, ha
, akkor negatív, ha 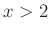 , akkor pozitív.
, akkor pozitív. -
Meghatározzuk a tört előjelét. Egy tört előjelét a számlálójának és a nevezőjének az előjele szabja meg. Tehát a deriváltfüggvény a
![$ ]-\infty ;-10[$](/images/stories/latex/0dc55236fbc2f5ae35755e2207cc48ca_dekanyevaamatekmiattnemleszdiplomam/img28.png) és a
és a ![$ ]2;\infty [$](/images/stories/latex/0dc55236fbc2f5ae35755e2207cc48ca_dekanyevaamatekmiattnemleszdiplomam/img29.png) intervallumokon negatív lesz, a
intervallumokon negatív lesz, a ![$ ]-10;-1[$](/images/stories/latex/0dc55236fbc2f5ae35755e2207cc48ca_dekanyevaamatekmiattnemleszdiplomam/img30.png) és a
és a ![$ ]-1;2[$](/images/stories/latex/0dc55236fbc2f5ae35755e2207cc48ca_dekanyevaamatekmiattnemleszdiplomam/img31.png) intervallumokon pozitív lesz.
intervallumokon pozitív lesz. - ...
Vegyük észre, hogy a megoldáshoz szükséges nyolc lépés közül az első és az utolsó kivételével a többi csak a középiskolai anyag ismeretét igényli.
Integrálszámítás
Az integrálszámítás nem könnyű része a matematikának, mert kevés általános szabály létezik. Például csak speciális alakú szorzat, hányados és hatvány integrálására van megfelelő képlet. Így ebben a témakörben különösen fontos, hogy a hatványok értelmezését és azonosságait jól tudjuk és az algebrai átalakításokban is jártasak legyünk Nulladik szabálynak szoktam nevezni, hogy az integrálandó szorzatot, hányadost, hatványt végezzük el, ha lehet, mert így alapintegrálokra tudjuk visszavezetni az eredeti problémát.
Hatványfüggvény integráljára visszavezethető feladatok
Elvégezhető szorzat integrálása:
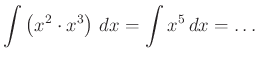
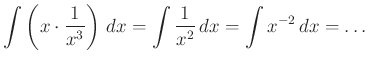
Elvégezhető hányados integrálása:
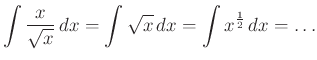
Elvégezhető hatvány integrálása:
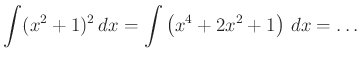
Ezek kombinálásával nagyon bonyolultnak tűnő feladatokat is meg tudunk oldani. Például:
![$\displaystyle \int\left(\sqrt[3]{\dfrac{\sqrt {x^{9}\cdot \sqrt x}}{x^{2}\cdot\sqrt[8]{x}}}\cdot \sqrt[8]{x^{9}}\right)\,dx=?
$](/images/stories/latex/0dc55236fbc2f5ae35755e2207cc48ca_dekanyevaamatekmiattnemleszdiplomam/img36.png)
- Először írjuk fel a gyököket törtkitevőjű hatványként:
![$\displaystyle \int\left(\sqrt[3]{\dfrac{\sqrt {x^{9}\cdot \sqrt x } }{x^{2}\cdo...
...2}\cdot x^{\frac{1}{8}}}\right)^{\frac{1}{3}}\cdot x^{\frac{9}{8}}\right)\,dx=
$](/images/stories/latex/0dc55236fbc2f5ae35755e2207cc48ca_dekanyevaamatekmiattnemleszdiplomam/img37.png)
- Majd a számlálóban és a nevezőben is alkalmazzuk az azonos alapú hatványok szorzására vonatkozó azonosságot, majd a hatvány hatványára vonatkozót:
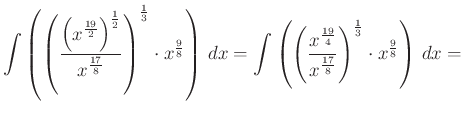
- Majd az azonos alapú hatványok hányadosára vonatkozó azonosságot, majd a hatvány hatványára vonatkozót, majd az azonos alapú hatványok szorzatára vonatkozót:
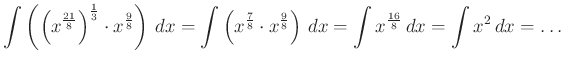
Vegyük észre, hogy a megoldáshoz szükséges sok lépés közül egyedül az utolsó lesz az, melyet nem tudunk megtenni pusztán csak középiskolai érettségi anyagának ismeretében.
Végezetül önmagamat ismételném. Írásomnak az a célja, hogy arra buzdítsam kollégáimat és az egyetemre készülő diákokat, hogy az algebra témakörét kiemelten kezeljék. Remélem sikerült meggyőznöm az érdeklődőket, hogy milyen algebrai ismeretekre, hol és miért van óriási szükség. Ha a diákok úgy érzik, további gyakorlásra van szükségük a középszintű érettségin túl, akkor minél előbb tegyék meg. Ne az egyetemen, az első kudarcok után szembesüljenek azzal, hogy a középiskolai hiányosságaik akadályozzák meg őket az egyetemi tananyag sikeres teljesítésében.
Dékány Éva
Szent István Egyetem









