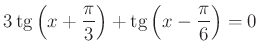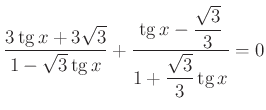A 2017. évi székesfehérvári vándorgyűlésen elhangzott előadás szerkesztett változata
Mottó: „A legtöbb amit a tanár a diákjaiért tehet az, hogy észrevétlenül rávezeti egy-egy jó ötletre.” (Pólya György)
Ha egy feladatnak megtaláltuk a megoldását, ha egy állítást bebizonyítottunk, a legtöbb esetben ezzel nem zárult le a kérdés. Szinte mindig érdemes még tovább foglalkozni a problémával, további kérdéseket feltenni. Ha kreatív szakembereket akarunk képezni, akkor erre feltétlenül érdemes rászoktatni a tanítványainkat.
Természetesen az az ideális, ha a feladat megoldását, a bizonyítás lehetséges módját nem közöljük a tanulókkal, hanem csak segítjük őket, hogy felfedezzék a célravezető utat. Ekkor lesz a belátott ismeret is, és a célhoz vezető módszer is a tanulónak igazán sajátja, ekkor várható, hogy ezeket újabb problémák megoldásában használni tudja. De sajnos nincs mindig időnk arra, hogy kivárjuk, amíg a tanulók többsége maga fedezi fel a megoldás útját. Ha mi mutattuk meg a megoldást, akkor is sok haszonnal jár, ha továbbgondoljuk a problémát. A megoldás menetének áttekintése, további kérdések felvetése sokat segíthet abban, hogy mind az alkalmazott módszer, mind a kapott eredmény alkalmazásképes ismeretté váljon. Sőt a jó kérdések újabb hasznos ismeretekhez vezethetnek, kiválóan fejlesztik a kreativitást.
A kérdéseket először mi tesszük fel, majd fokozatosan érjük el, hogy ezeket már a tanulók maguk fogalmazzák meg. Ha ezt következetesen csináljuk, akkor eljuthatunk ahhoz az örömteli helyzethez, hogy a tanítványaink olyan érdekes kérdéseket is fel tudnak tenni, ami nekünk nem is jutott eszünkbe.
Néhány javasolt kérdés, amit célszerű feltenni
- Lehet-e a feladatnak több, más eredménye is?
- Lehet-e más módszerrel eredményre jutni? Melyik módszer a legalkalmasabb, melyik ragadja meg leginkább a feladat lényegét?
- Milyen más feladatokban vezethet eredményre a megoldásban alkalmazott módszer?
- Szükség volt-e a megoldáshoz minden feltételre?
- Lehet-e a problémát általánosítani?
- Megfordítható-e az állítás?
- Hogyan változhat a feladat eredménye, vagy megoldási módszere, ha a feltételeket kissé módosítjuk?
- Milyen alkalmazásai lehetnek a megoldott problémának?
A továbbiakban bemutatok néhány példát arra, amikor tanítási vagy feladatkitűzői tevékenységem során a fenti kérdések tanulságos válaszokhoz vezettek. A példákat két cikkben mutatom be. Az elsőben a kérdéssor első részéhez mutatok példákat, a másodikban majd a további kérdésekkel foglalkozunk, amelyek kissé más típusú továbbgondolási lehetőségekre vezetnek.
I. Lehet-e a feladatnak több, más megoldása (eredménye) is?
Ha megtaláltuk a feladatnak egy megoldását, akkor természetesen fel kell tennünk ezt a kérdést. Mégis, a legjobb tanulóknál is előfordul, hogy ez a kérdés elmarad, vagy felteszik ugyan a kérdést, de nem találják meg az összes megoldást. Sőt feladatgyűjteményekben is előfordul a nem teljes megoldás. Így volt ez a következő feladatnál is.
I/1. feladat. Adott az ![]() középpontú,
középpontú, ![]() sugarú
sugarú ![]() kör és az
kör és az ![]() középpontú,
középpontú, ![]() sugarú
sugarú ![]() kör, (
kör, ( ![]() ). A két kör
). A két kör ![]() és
és ![]() pontokban metszi egymást. Az
pontokban metszi egymást. Az ![]() pontra illeszkedő egyenesek közül melyiknek lesz a két körlemez egyesítésébe eső darabja a leghosszabb?
pontra illeszkedő egyenesek közül melyiknek lesz a két körlemez egyesítésébe eső darabja a leghosszabb?
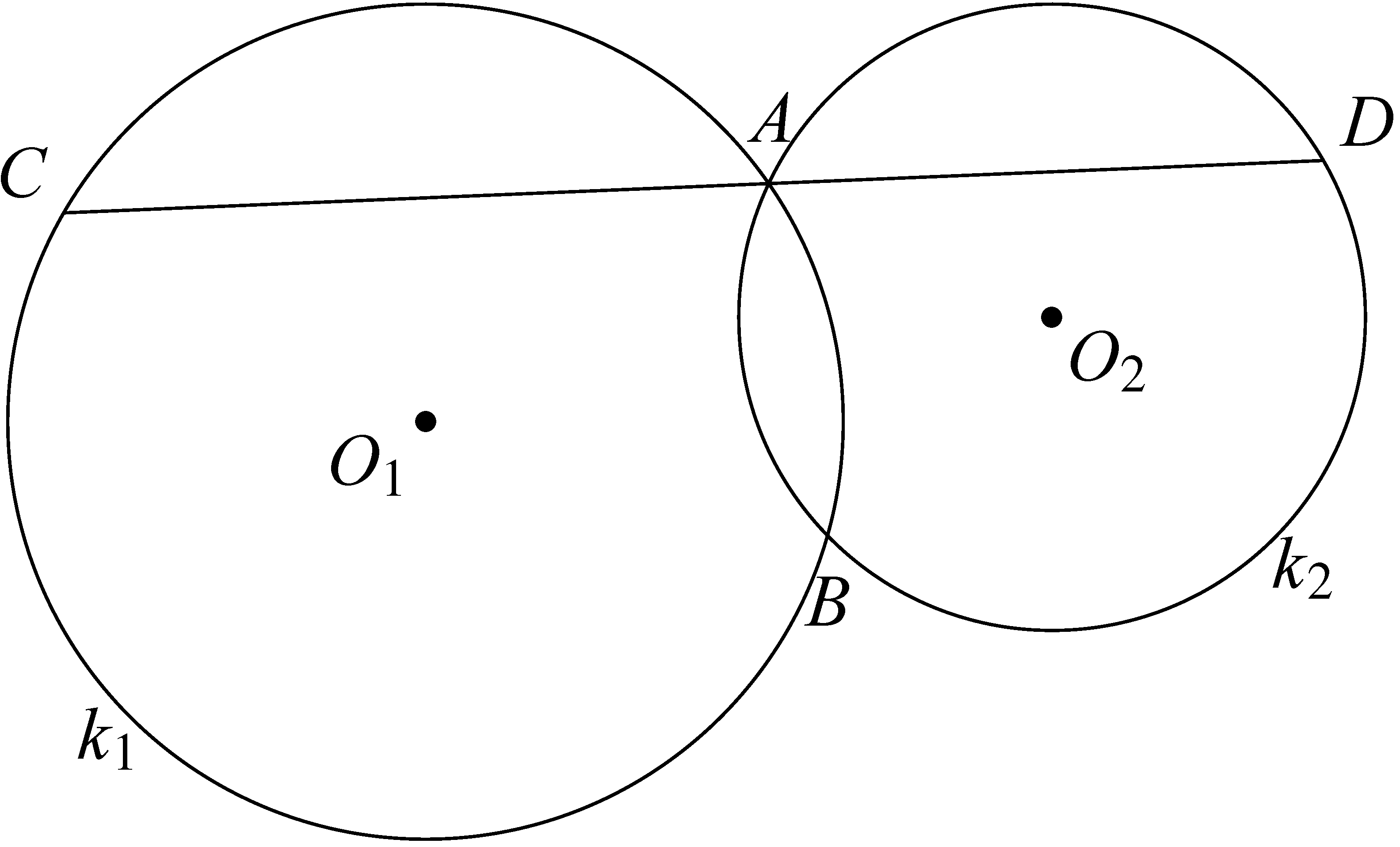
a) A szokásos megoldás:
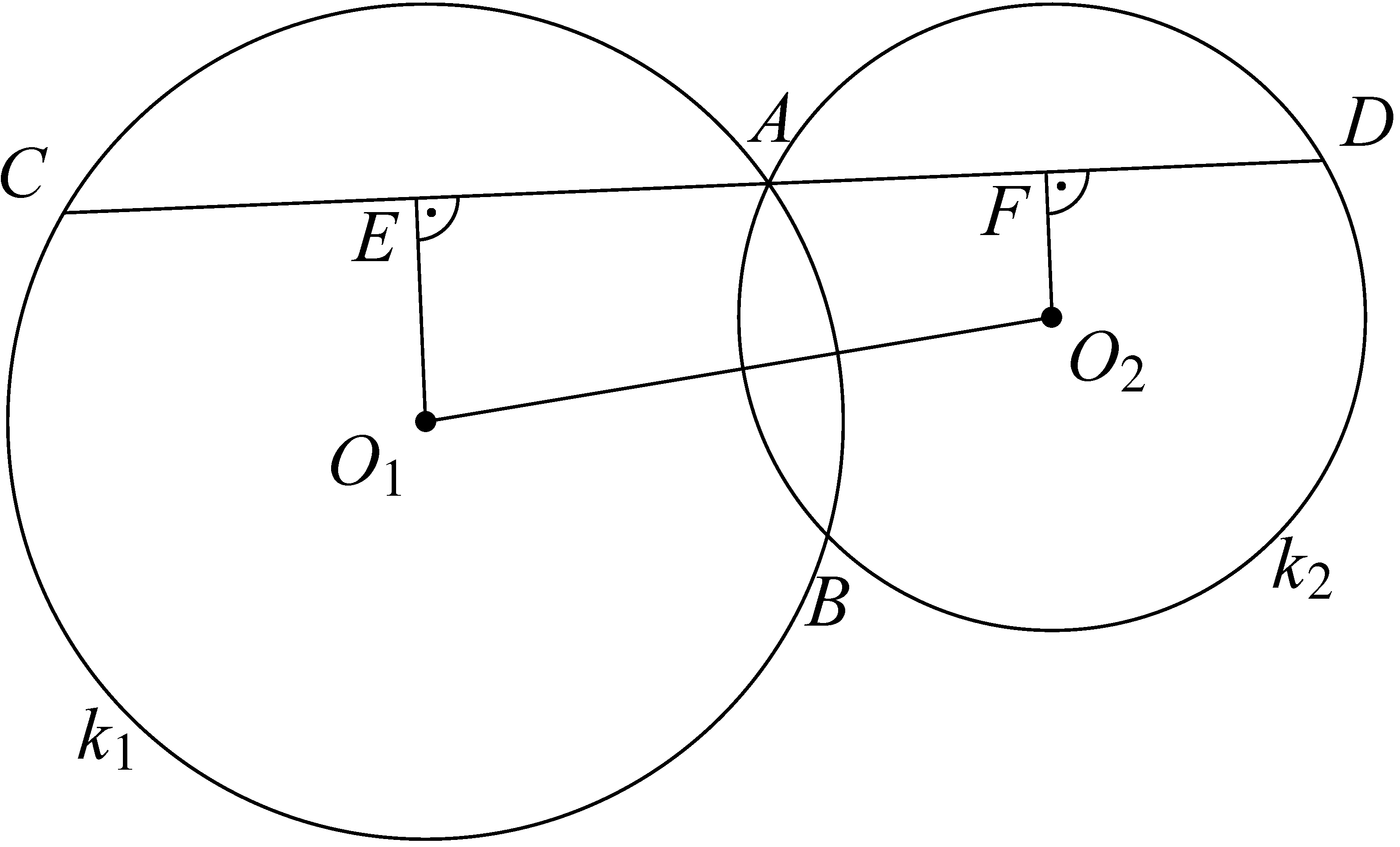
Állítsunk merőlegeseket a két középpontból a szelőre! Az így kapott ![]() derékszögű trapézban
derékszögű trapézban ![]() . Egyenlőség akkor és csak akkor állhat, ha
. Egyenlőség akkor és csak akkor állhat, ha ![]() .
.
Másrészt ![]() és
és ![]() a húrdarabok felezőpontjai, ezért
a húrdarabok felezőpontjai, ezért ![]() .
.
Ebből ![]() . Tehát az
. Tehát az ![]() pontra illeszkedő egyenesek közül annak lesz a két körlemez egyesítésébe eső darabja a leghosszabb, amely párhuzamos a két kör középpontját összekötő szakasszal. Ekkor a maximum
pontra illeszkedő egyenesek közül annak lesz a két körlemez egyesítésébe eső darabja a leghosszabb, amely párhuzamos a két kör középpontját összekötő szakasszal. Ekkor a maximum ![]() . A feltételeknek ez az egy egyenes felel meg.
. A feltételeknek ez az egy egyenes felel meg.
Feladatgyűjteményben is ez a megoldás jelent meg, és versenyen a tanulók többsége is ezt a megoldást adta. Már itt szükséges meggondolni, hogy ha a szelőnek van közös pontja az ![]() szakasszal, akkor az
szakasszal, akkor az ![]() derékszögű trapéz háromszöggé vagy konkáv, hurkolt trapézzá fajul.
derékszögű trapéz háromszöggé vagy konkáv, hurkolt trapézzá fajul.
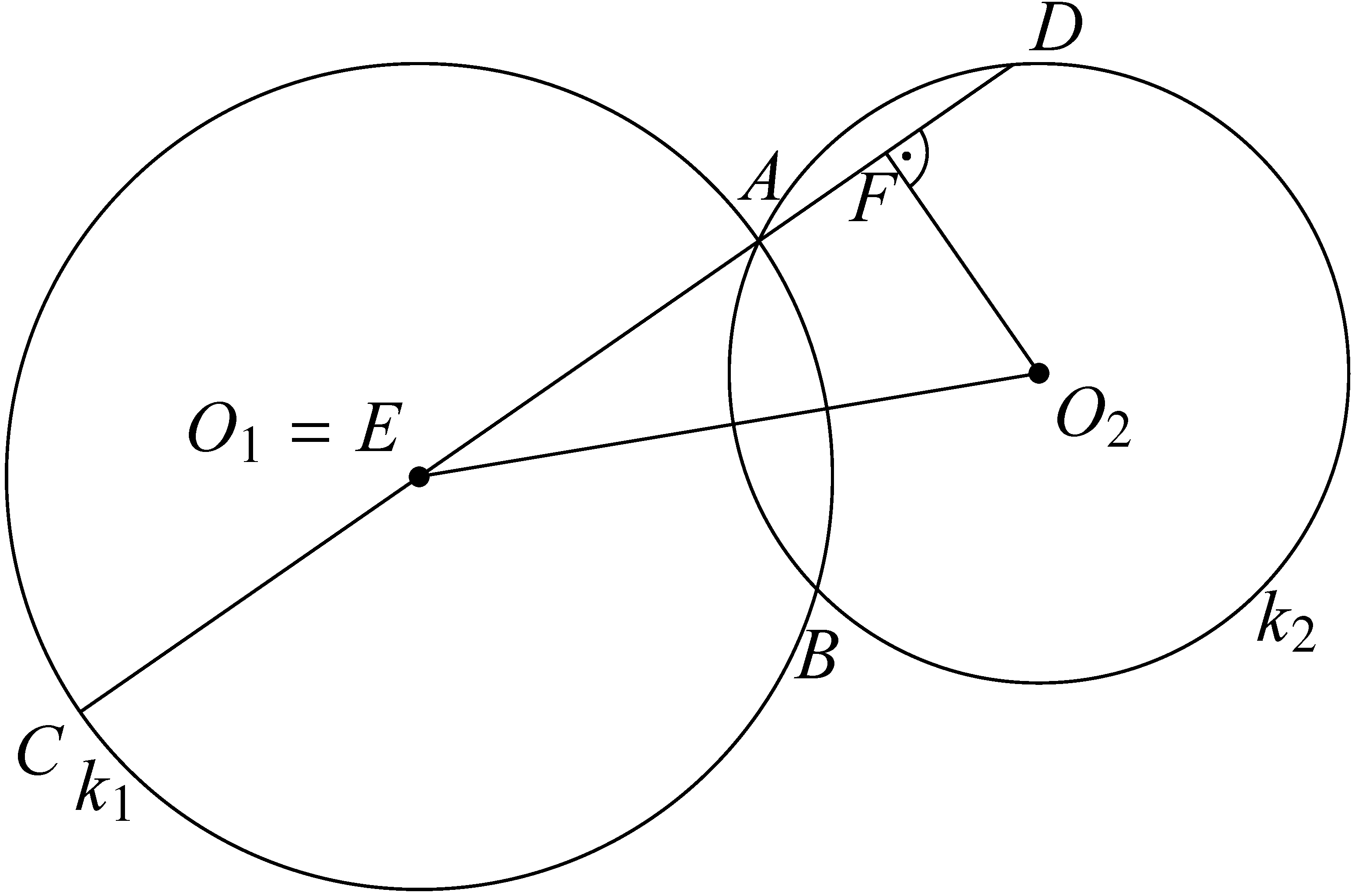
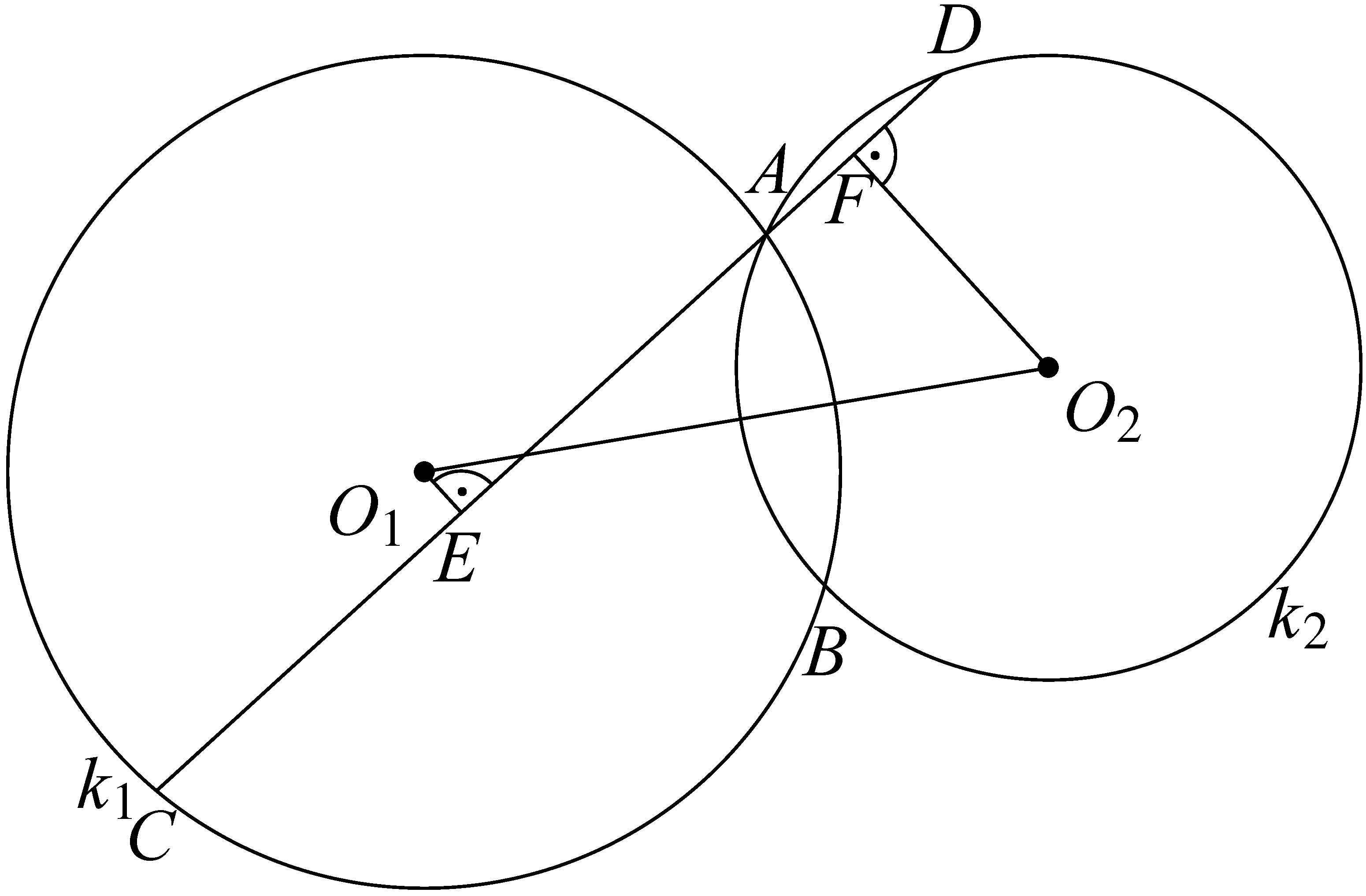
Az ábrákon látható, ezekben az esetekben ![]() . Tehát továbbra is érvényes, hogy a szelőnek a két körlemez egyesítésébe eső darabja nem lehet nagyobb
. Tehát továbbra is érvényes, hogy a szelőnek a két körlemez egyesítésébe eső darabja nem lehet nagyobb ![]() -nél.
-nél.
Egy minimális elemzés is gyanússá teheti, ezt a megállapításunkat. Nyilván, ez nem lehet jó, ha ![]() nagyon kicsi a sugarakhoz képest. Ez a megoldás csak akkor jó, ha
nagyon kicsi a sugarakhoz képest. Ez a megoldás csak akkor jó, ha ![]() nagyobb a nagyobb kör sugaránál. Mi a helyzet a többi esetben?
nagyobb a nagyobb kör sugaránál. Mi a helyzet a többi esetben?
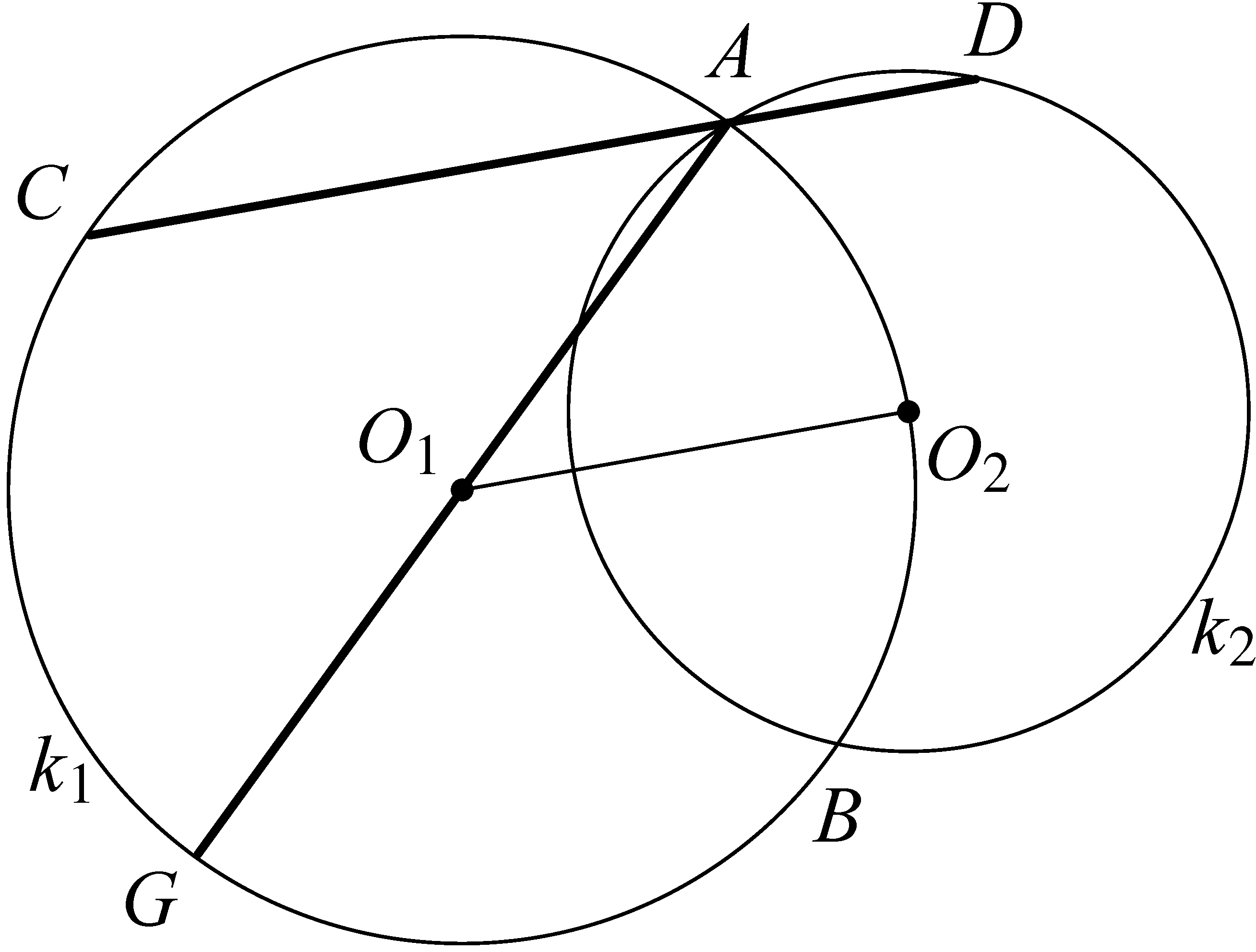
b) Ha ![]() :
:
Ez esetben az ![]() szakasszal párhuzamos szakasz:
szakasszal párhuzamos szakasz: ![]() , de ugyanilyen hosszúságú a
, de ugyanilyen hosszúságú a ![]() kör
kör ![]() átmérője is. Tehát ebben az esetben két megoldás van.
átmérője is. Tehát ebben az esetben két megoldás van.

c) Ha ![]() :
:
Ez esetben az ![]() szakasszal párhuzamos szakasz:
szakasszal párhuzamos szakasz: ![]() , de ugyanilyen hosszúságú a
, de ugyanilyen hosszúságú a ![]() kör
kör ![]() átmérője és a
átmérője és a ![]() kör
kör ![]() átmérője is. Tehát ebben az esetben három megoldás van.
átmérője is. Tehát ebben az esetben három megoldás van.
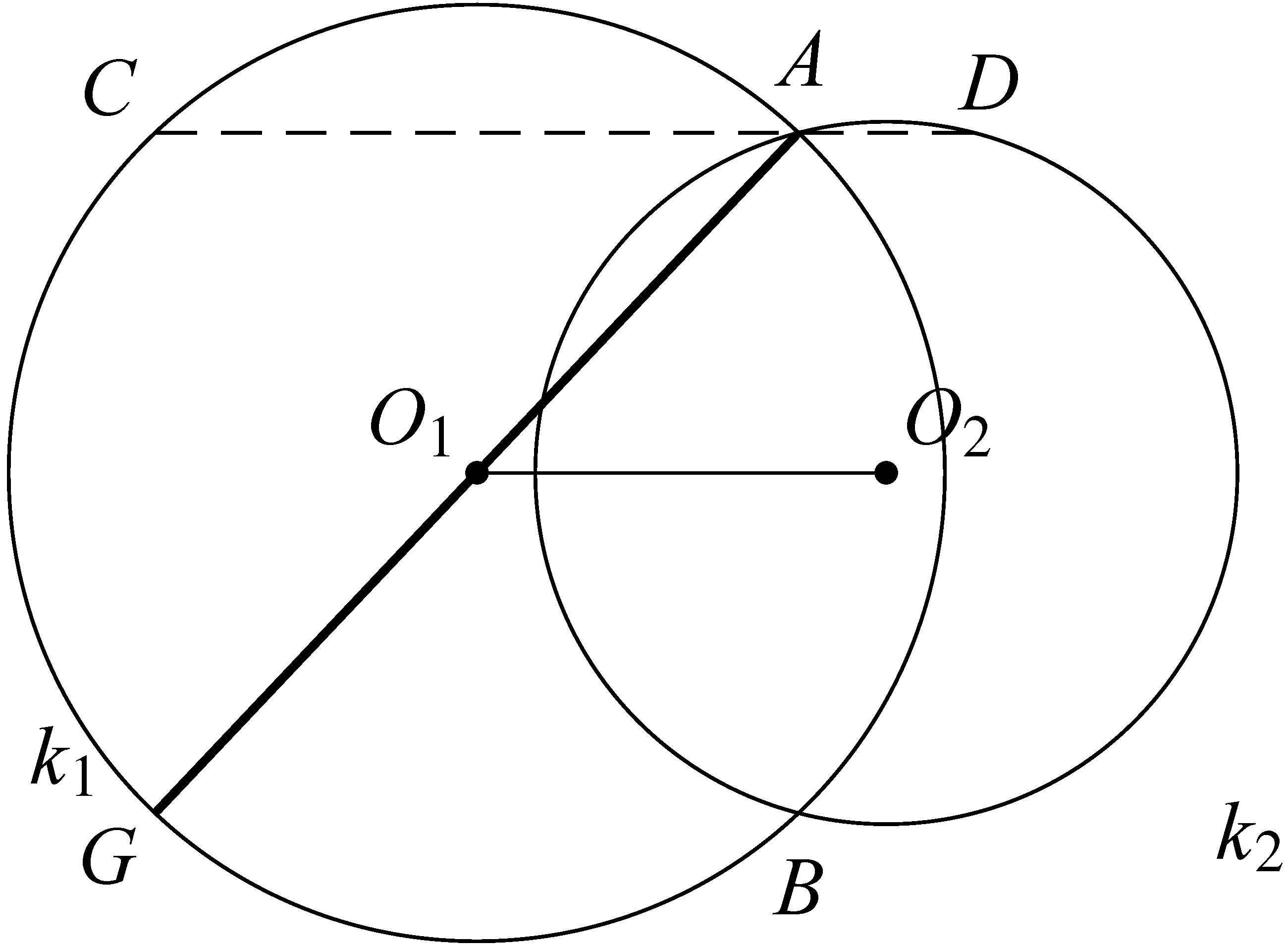
d) Ha ![]() és
és ![]() :
:
Ez esetben az ![]() szakasszal párhuzamos szakasz:
szakasszal párhuzamos szakasz: ![]() , ezért csak a
, ezért csak a ![]() kör
kör ![]() átmérője a megoldás. Tehát ebben az esetben egy megoldás van.
átmérője a megoldás. Tehát ebben az esetben egy megoldás van.
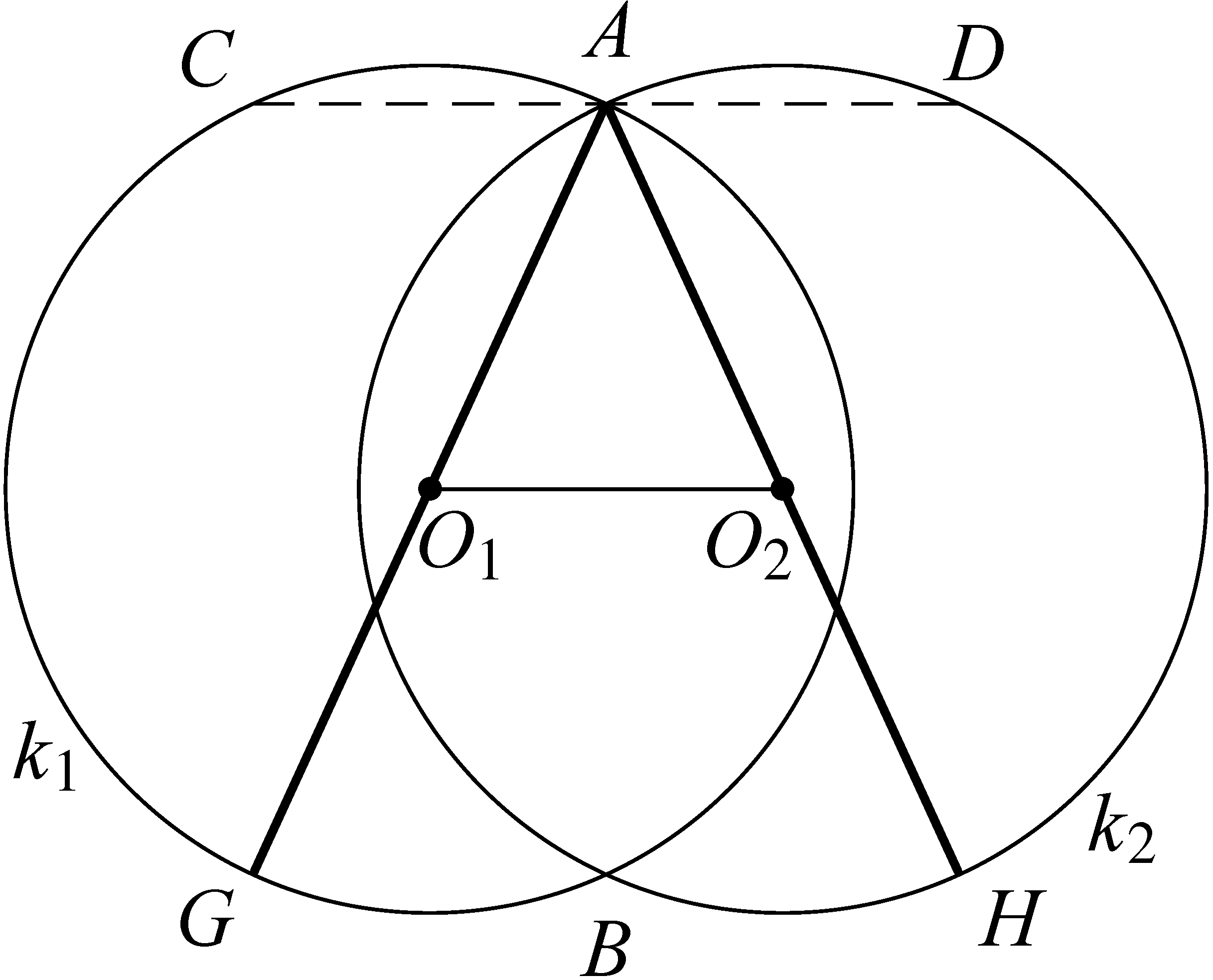
e) Ha ![]() :
:
Ez esetben az ![]() szakasszal párhuzamos szakasz:
szakasszal párhuzamos szakasz: ![]() , ezért most a
, ezért most a ![]() kör
kör ![]() átmérője és a
átmérője és a ![]() kör
kör ![]() átmérője a megoldás. Tehát ebben az esetben két megoldás van.
átmérője a megoldás. Tehát ebben az esetben két megoldás van.
(A feladatot kitűztem a Fejér Lipót Matematikaversenyen 2005-ben a 11. évfolyam számára, de nem született teljes megoldás.)
A következő feladat is a Fejér Lipót Matematikaversenyen szerepelt 2004-ben a 12. évfolyam számára, de erre sem kaptunk teljes megoldást.
I/2. feladat. Oldjuk meg a következő egyenletet a valós számok halmazán!
Alkalmazzuk a 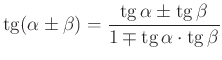 összefüggéseket!
összefüggéseket!
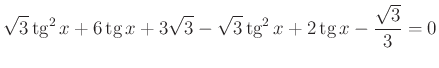
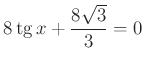
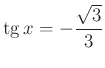
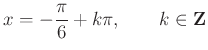
Ellenőrzéssel meggyőződhetünk, hogy a kapott gyökök kielégítik az egyenletet.
De az is látható, hogy 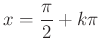 is kielégíti az egyenletet. Hogyan lehetséges ez, hol veszett el ez a gyök?
is kielégíti az egyenletet. Hogyan lehetséges ez, hol veszett el ez a gyök?
A 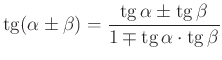 összefüggések alkalmazásánál az értelmezési tartomány szűkebb lesz! A bal oldal értelmezve van, ha
összefüggések alkalmazásánál az értelmezési tartomány szűkebb lesz! A bal oldal értelmezve van, ha ![]() és
és ![]() közül csak az egyik
közül csak az egyik 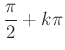 alakú, de a jobb oldal ez esetben nincs értelmezve. Ezért ezeknek az összefüggéseknek az alkalmazásakor meg kell vizsgálnunk, nem vesztettünk-e gyököt, azaz hogy azok a számok, amelyekkel az értelmezési tartomány szűkebb lett, megoldásai-e az eredeti egyenletnek.
alakú, de a jobb oldal ez esetben nincs értelmezve. Ezért ezeknek az összefüggéseknek az alkalmazásakor meg kell vizsgálnunk, nem vesztettünk-e gyököt, azaz hogy azok a számok, amelyekkel az értelmezési tartomány szűkebb lett, megoldásai-e az eredeti egyenletnek.
Látható, 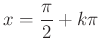 az eredeti (
az eredeti (![]() ) egyenletnek gyöke, de (
) egyenletnek gyöke, de (![]() )-nek és a következőknek már nem. Tehát az (
)-nek és a következőknek már nem. Tehát az (![]() ) egyenlet gyökei
) egyenlet gyökei 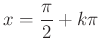 és
és 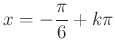 , ahol
, ahol ![]() .
.
Igen hasznosnak találom, ha versenyeken ilyen típusú feladat is szerepel, amelyben egy megoldást könnyű megtalálni, de a teljes megoldás komolyabb elemzést igényel. Így sok tanulónak van sikerélménye egy megoldás megtalálásával, de a legjobbak között lehet különbséget tenni aszerint, hogy meddig jutnak el a teljes megoldásból. Azért is jó, ha ilyen feladatok versenyeken szerepelnek, mert a teljes megoldáshoz szükséges elemzés azokban is megmarad, akik csak részeredményekig jutottak.
A következő, szintén a Fejér Lipót Versenyről választott feladatokban is könnyű egy megoldást találni, de a teljes megoldás megtalálása komolyabb odafigyelést követel. Ezen feladatok megoldását az olvasóra hagyjuk, illetve megtalálhatók [1]-ben.
I/3. feladat. Vizsgáljuk meg, hogy a ![]() paraméter különböző értékei esetén hány megoldása lesz a
paraméter különböző értékei esetén hány megoldása lesz a ![]() egyenletnek a
egyenletnek a ![]() intervallumon?
intervallumon?
I/4. feladat. A ![]() valós paraméter milyen értékei esetén lesz pontosan egy valós gyöke a következő egyenletnek?
valós paraméter milyen értékei esetén lesz pontosan egy valós gyöke a következő egyenletnek?
I/5 feladat. Az ![]() valós paraméter mely értékei esetén van pontosan egy valós megoldása a következő egyenletnek?
valós paraméter mely értékei esetén van pontosan egy valós megoldása a következő egyenletnek?
A következő részben több egymással összefüggő, egymást kiegészítő továbbgondolási lehetőséget tekintünk át.
II. Lehet-e más módszerrel eredményre jutni?
Melyik módszer ragadja meg leginkább a feladat lényegét?
Milyen más feladatokban vezethet eredményre a megoldásban alkalmazott módszer?
Szükség volt-e a megoldáshoz minden feltételre?
Elég természetes dolog matematikatanításunkban, hogy egy feladatnak többféle megoldását is keressük. Már csak azért is, mert lehet, hogy egy másik, hasonlónak tűnő feladatnál valamelyik módszer nem működik, akkor legyen kéznél más módszer is.
Erdős Pál szerint Istennek van egy könyve, és abban szerepel minden feladatnak a Megoldása. Az igazi, a legszebb, legelegánsabb Megoldás. Egy matematikus ne elégedjen meg azzal, hogy egy problémának megtalálja egy megoldását, törekedjen a Könyvben levő Megoldás megtalálására. Tanítványainkat is próbáljuk rávenni, arra, hogy a feladatoknak keressék az alapgondolatát, a feladat szellemiségéhez leginkább közelítő megoldását. Próbáljuk kitalálni, hogy mire is gondolt a feladat kitűzője.
A következő feladatoknak többféle megoldását is megadjuk, illetve keressük a feladat alapgondolatához leginkább közelítő megoldást.
II/1. feladat. Az ![]() ,
, ![]() ,
, ![]() valós számokra teljesül, hogy
valós számokra teljesül, hogy ![]() . Igazoljuk, hogy ezekre a számokra
. Igazoljuk, hogy ezekre a számokra ![]() is teljesül!
is teljesül!
1. megoldás. A szokásos megoldás az, hogy a feltételt alakítjuk addig, amíg megkapjuk az állítást.
Ez esetben nem látszik rögtön a célravezető út. Az látszik, hogy a kisebb oldalon a ![]() kifejezés kialakítható
kifejezés kialakítható
| 0 | ||
| 0 |
Ha mindkét oldalhoz ![]() -et adunk, akkor már az állítás minden eleme szerepelni fog.
-et adunk, akkor már az állítás minden eleme szerepelni fog.
Innen már látható a megoldás: ![]() .
.
2. megoldás. Ha egy feltételből kell egy állításhoz eljutni, akkor az indirekt bizonyítási mód is sokszor célra vezet. Tegyük fel, hogy a feltétel igaz, de az állítás nem igaz, és ebből jussunk ellentmondásra.
Tegyük fel, hogy az állítás nem igaz: ![]() . Adjuk ezt össze a feltételben szereplő
. Adjuk ezt össze a feltételben szereplő ![]() egyenlőtlenség 4-szeresével!
egyenlőtlenség 4-szeresével!
Egy négyzetszám nem lehet negatív, így ellentmondásra jutottunk.
3. megoldás. Ha az állítást ![]() alakban írjuk, akkor kézenfekvő, hogy a megoldást a másodfokú egyenletek, függvények témakörben keressük.
alakban írjuk, akkor kézenfekvő, hogy a megoldást a másodfokú egyenletek, függvények témakörben keressük.
Tekintsük az ![]() függvényt!
függvényt!
Ha ![]() , akkor a feltétel miatt nem lehet
, akkor a feltétel miatt nem lehet ![]() is 0, ezért a
is 0, ezért a ![]() állítás teljesül.
állítás teljesül.
Ha ![]() , akkor
, akkor ![]() és
és ![]() , ezek a feltétel szerint különböző előjelűek. Ha egy másodfokú függvény pozitív és negatív értéket is felvesz, akkor van két zérushelye, ezért diszkriminánsa
, ezek a feltétel szerint különböző előjelűek. Ha egy másodfokú függvény pozitív és negatív értéket is felvesz, akkor van két zérushelye, ezért diszkriminánsa ![]() .
.
(Talán joggal feltételezhetjük, hogy a kitűző erre a megoldásra gondolt.)
II/2. feladat. ![]() ,
, ![]() ,
, ![]() olyan pozitív valós számok, amelyekre
olyan pozitív valós számok, amelyekre
Határozzuk meg ![]() értékét!
értékét!
1. megoldás. Az ![]() kifejezés az
kifejezés az ![]() kifejezés szorzat alakjának egyik tényezője, ezért szorozzuk az egyenleteket rendre
kifejezés szorzat alakjának egyik tényezője, ezért szorozzuk az egyenleteket rendre ![]() ,
, ![]() ,
, ![]() -szel!
-szel!
Összeadva:
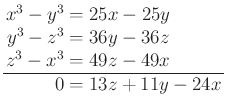
Ebből 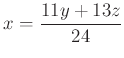 .
.
Helyettesítsük ezt vissza az eredeti első egyenletbe:
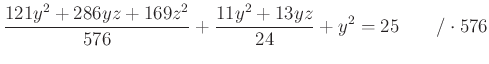
A
egyenletrendszerben a konstanst érdemes kiküszöbölni.
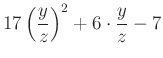 |
Ennek pozitív megoldása 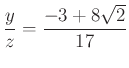 , ebből
, ebből 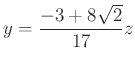 .
.
Ezt behelyettesítve az ![]() egyenletbe, a
egyenletbe, a ![]() -re kapott másodfokú egyenlet pozitív gyöke
-re kapott másodfokú egyenlet pozitív gyöke 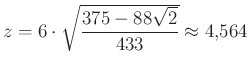 .
.
Ebből 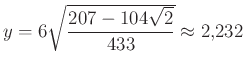 ,
, 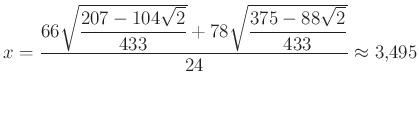 .
.
Ezekből ![]() . 1
. 1
2. megoldás. Ezúttal geometriai, illetve trigonometriai meggondolásokat alkalmazunk.
Az egyenletek egy-egy olyan háromszögre felírt koszinusz-tételek, amelyekben az 5, 6, 7 egység hosszúságú oldalakkal szemben rendre ![]() -os szög van.
-os szög van.
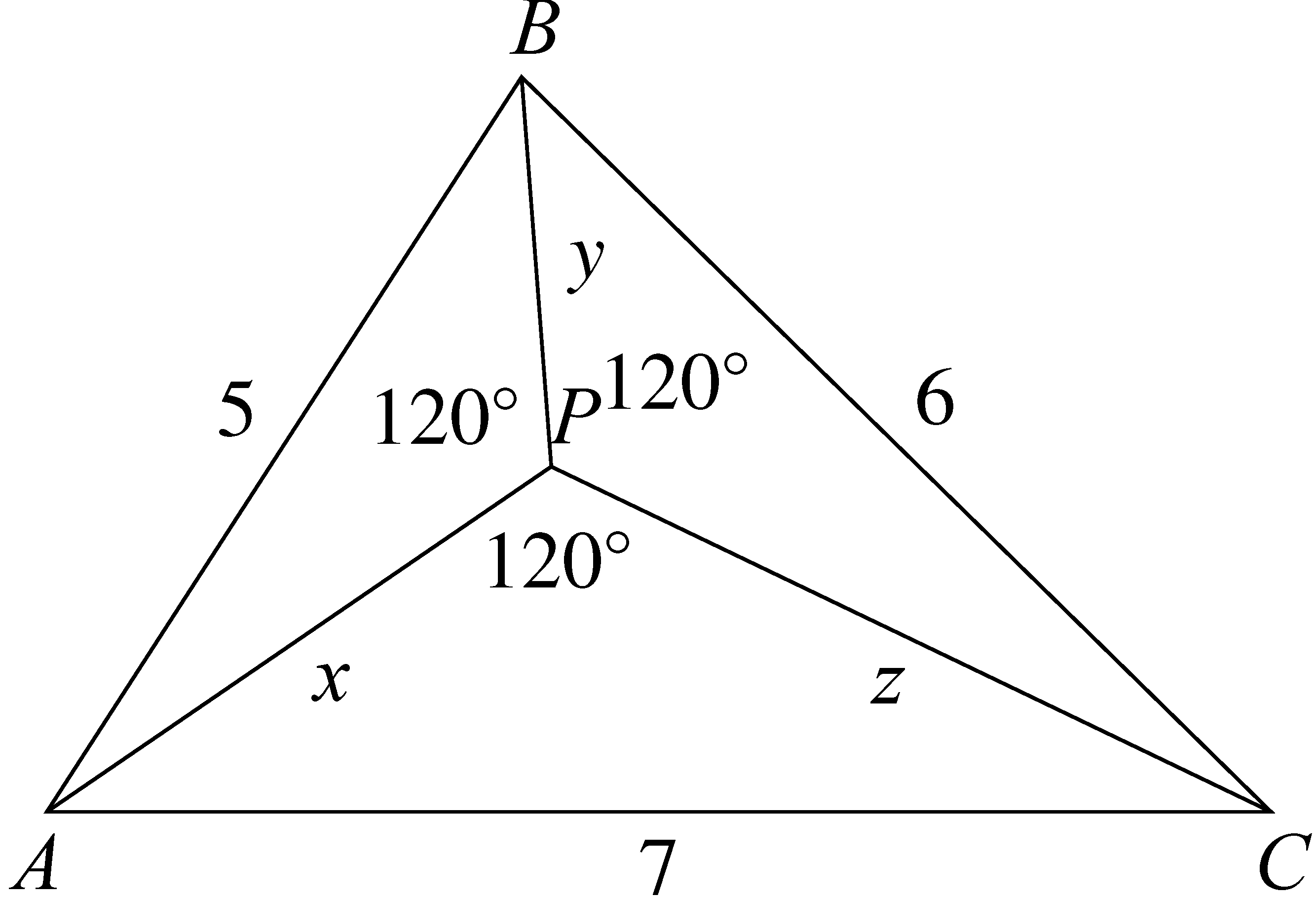 Az 5, 6, 7 egység oldalú
Az 5, 6, 7 egység oldalú ![]() háromszögben
háromszögben ![]() legyen az a pont, amelyből az oldalak
legyen az a pont, amelyből az oldalak ![]() -os szögben látszanak.2
-os szögben látszanak.2
Ekkor az egyenletekben szereplő ismeretlenek éppen az ![]() ,
, ![]() ,
, ![]() értékeket adják.
értékeket adják.
Az egyenletrendszernek csak egy pozitív számhármas a megoldása3, tehát ezek ![]() ,
, ![]() és
és ![]() .
.
Mekkora ![]() értéke?
értéke?
Számítsuk ki az ![]() háromszög területét kétféleképpen: Héron-képlettel és a kis háromszögekre felírt trigonometrikus területképletek összegeként:
háromszög területét kétféleképpen: Héron-képlettel és a kis háromszögekre felírt trigonometrikus területképletek összegeként:
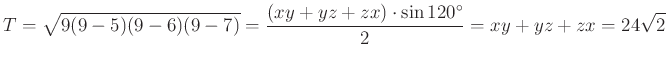
Ebből ![]() .
.
(Talán erről a megoldásról feltételezhetjük, hogy a Könyvből való.)
A trigonometria alkalmazása algebrai feladatok megoldását sokszor könnyebbé teszi. Most egy algebrai egyenlőtlenség és egy szélsőérték-feladat megoldására mutatunk trigonometrikus megoldást.
II/3. feladat. Igazoljuk, hogy három pozitív valós szám közül mindig kiválasztható kettő, ![]() és
és ![]() , amelyekre
, amelyekre 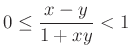 teljesül!
teljesül!
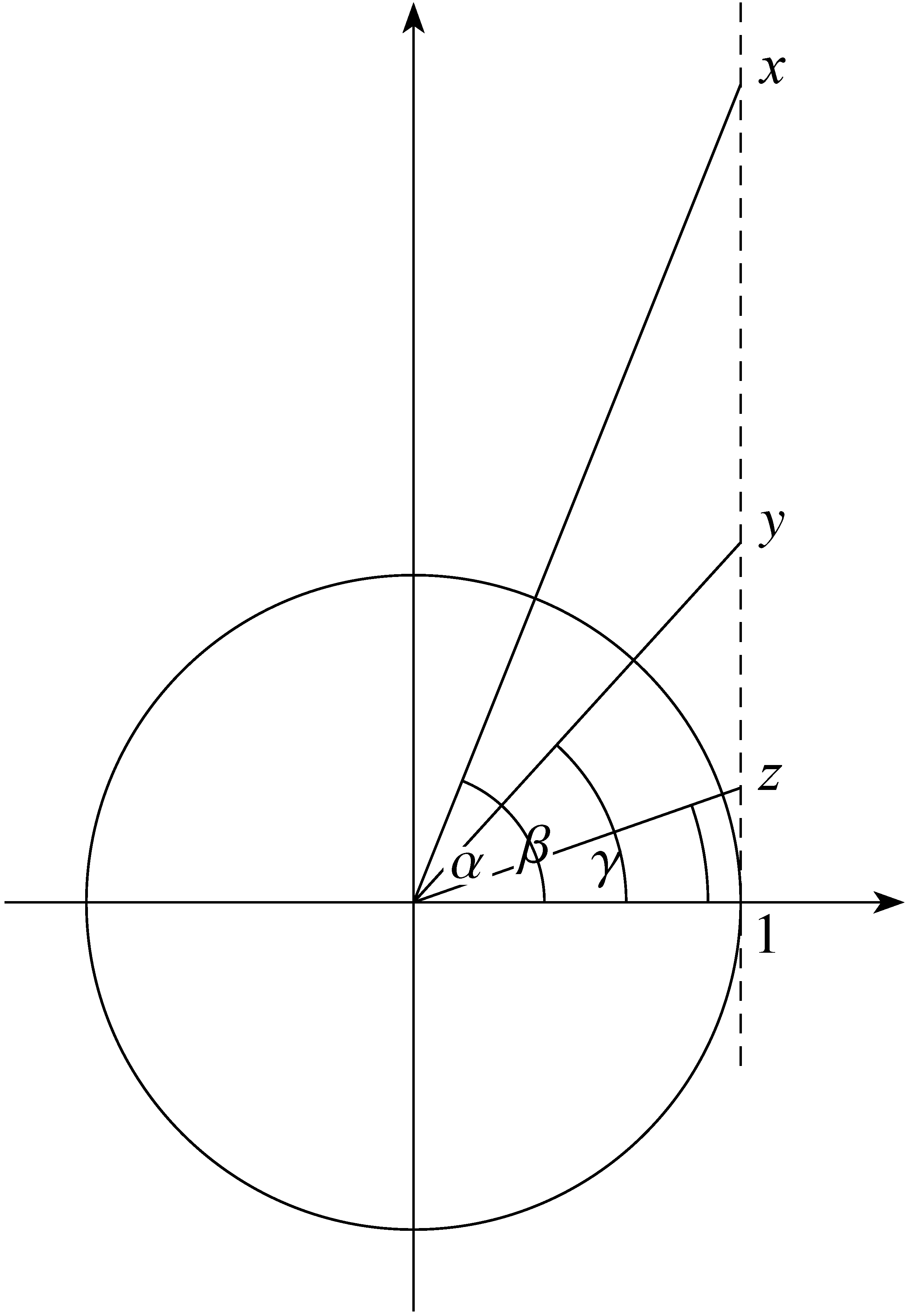
Az 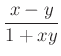 kifejezés sugallja a
kifejezés sugallja a ![]() összefüggés alkalmazását.
összefüggés alkalmazását.
Ha a három pozitív szám ![]() ,
, ![]() ,
, ![]() , akkor
, akkor ![]() ,
, ![]() ,
, ![]() legyenek azok a hegyesszögek, amelyekre
legyenek azok a hegyesszögek, amelyekre ![]() ,
, ![]() ,
, ![]() .
.
A három hegyesszög között mindig van két olyan, amelyek különbsége kisebb ![]() -nál. Ha például
-nál. Ha például ![]() , akkor
, akkor ![]() . Ez pedig éppen a bizonyítandó egyenlőtlenséget adja.
. Ez pedig éppen a bizonyítandó egyenlőtlenséget adja.
Látható az is, hogy az alsó határ akkor érhető el, ha a számok között van két egyenlő. A felső határ nem csökkenthető, mert ha ![]() ,
, ![]() ,
, ![]() , akkor
, akkor ![]() és
és ![]() , ezért mindkét hányados tetszőlegesen közel kerül 1-hez.
, ezért mindkét hányados tetszőlegesen közel kerül 1-hez.
A trigonometrikus megoldás ötletet adhat tisztán algebrai megoldás alkalmazására is.
2. megoldás. Három pozitív szám között mindig van vagy kettő, amely 1-nél nem kisebb, vagy kettő, amely 1-nél nem nagyobb. Legyen ez a kettő ![]() és
és ![]() úgy, hogy
úgy, hogy ![]() .
.
Ha ![]() , akkor
, akkor 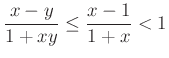 .
.
Ha ![]() , akkor
, akkor 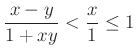 .
.
Joggal állíthatjuk, hogy itt az első megoldás fejezi ki jobban a feladatban rejlő gondolatot, és a geometriai ábra alapján könnyebben látható, hogy a felső határ nem csökkenthető.
Különösen ajánlott a trigonometrikus helyettesítés, ha ![]() alakú egyenlettel vagy feltétellel találkozunk.
alakú egyenlettel vagy feltétellel találkozunk.
Egy ilyen szélsőérték-feladatot is választottam, olyat, amelyben a szokásos elemi módszerek, például nevezetes közepek nem látszanak célravezetőnek, a trigonometrikus helyettesítés viszont szép megoldásra vezet.
II/4. feladat. Határozzuk meg az ![]() kifejezés maximumát, ha
kifejezés maximumát, ha ![]() és
és ![]() ,
, ![]() .
.
Megoldás. Az ![]() feltétel sugallja, hogy vezessük be az
feltétel sugallja, hogy vezessük be az ![]() ,
, ![]() helyettesítést! (
helyettesítést! ( ![]() ) Így a
) Így a ![]() kifejezés maximumát keressük a
kifejezés maximumát keressük a ![]() intervallumon.
intervallumon.
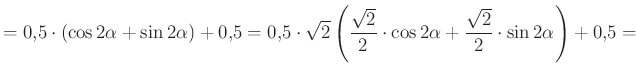 |
||
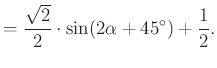 |
Ennek maximuma 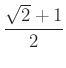 , ha
, ha ![]() , azaz ha
, azaz ha 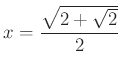 ,
, 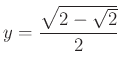 .
.
A következő feladat algebrai megoldása szintén nem kézenfekvő, de a geometria megoldás szép, elegáns.
II/5. feladat. Legyenek ![]() ,
, ![]() ,
, ![]() a
a ![]() intervallum tetszőleges számai. Mutassuk meg, hogy
intervallum tetszőleges számai. Mutassuk meg, hogy
A bal oldali egyenlőtlenség nyilvánvalóan igaz, hiszen mindhárom tag nem negatív. Csak a jobb oldali egyenlőtlenséggel foglakozunk.
1. megoldás (algebrai). A jobb oldali egyenlőtlenség bizonyításához vizsgáljuk a tagok két tényezőjét.
I. Ha van köztük olyan, amelyben az egytagú nem kisebb a másiknál, például
akkor végezzük a következő becslést
Az első egyenlőtlenség azért igaz, mert (![]() ) miatt az elhagyott tag nem pozitív. A második 0-ra redukálással, szorzattá alakítással látható be:
) miatt az elhagyott tag nem pozitív. A második 0-ra redukálással, szorzattá alakítással látható be: ![]() , és itt mindkét tényező nemnegatív.
, és itt mindkét tényező nemnegatív.
II. Ha minden a tagban az egytagú tényező kisebb a kéttagúnál: ![]() ,
, ![]() ,
, ![]() , akkor legyen
, akkor legyen ![]() ,
, ![]() ,
, ![]() , ebből
, ebből ![]() ,
, ![]() ,
, ![]() , és ekkor az egyenlőtlenség új alakja:
, és ekkor az egyenlőtlenség új alakja: ![]() . Itt viszont már
. Itt viszont már ![]() , ezért ez az egyenlőtlenség az I. pont szerint igazolható.
, ezért ez az egyenlőtlenség az I. pont szerint igazolható.
2. megoldás (geometriai). Mivel kéttényezős szorzatokat vizsgálunk, próbáljuk meg azokat területek mértékeként értelmezni! Tekintsünk egy 1 oldalú szabályos háromszöget, és ennek oldalain vegyük fel az ![]() ,
, ![]() ,
, ![]() hosszúságú szakaszokat.
hosszúságú szakaszokat.
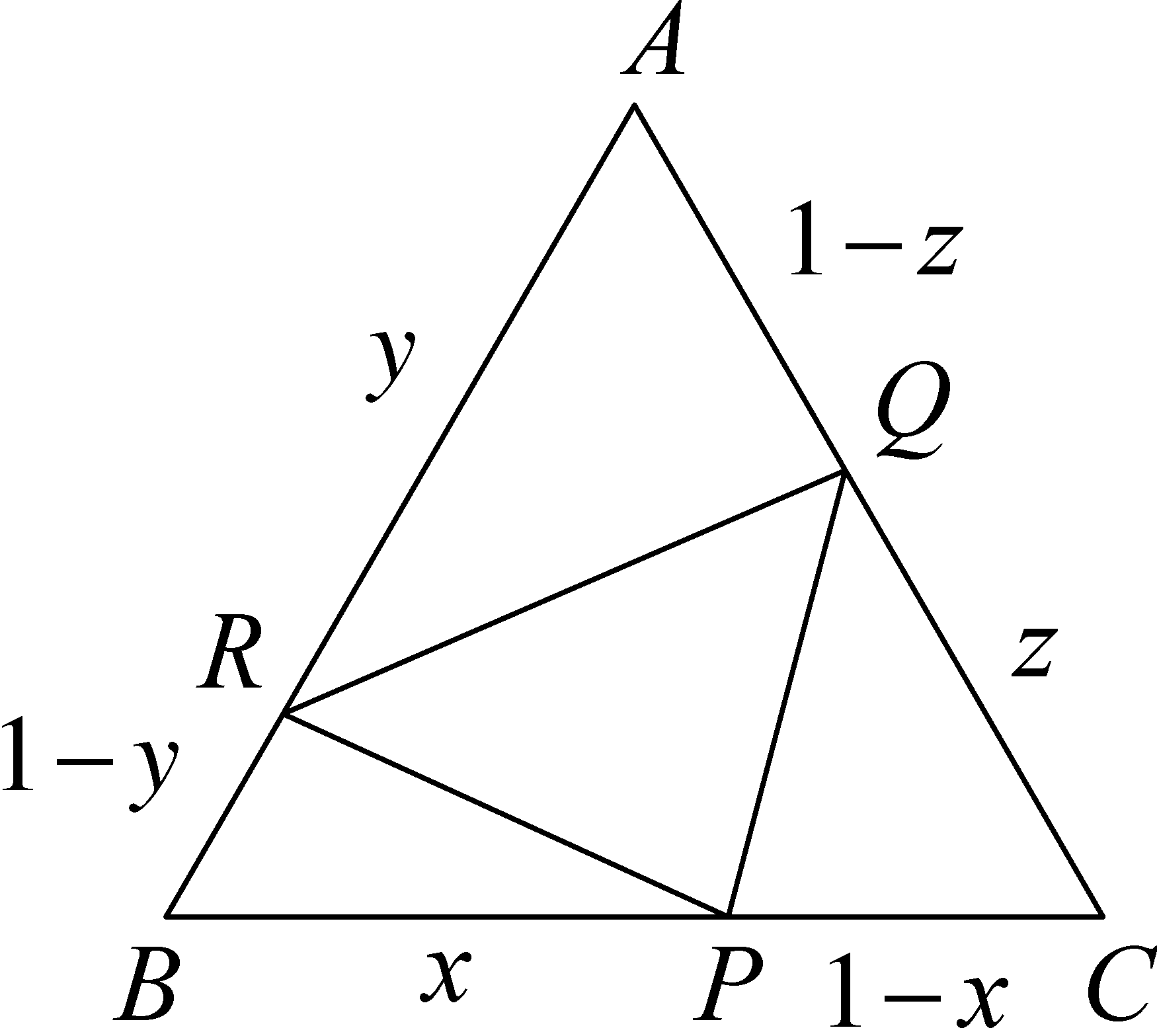
Ahhoz, hogy területeket tudjunk értelmezni, az ![]() egyenlőtlenség mindkét oldalát szorozzuk
egyenlőtlenség mindkét oldalát szorozzuk 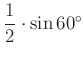 -kal!
-kal!
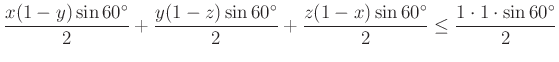
Az itt szereplő tagok, rendre a ![]() , az
, az ![]() , a
, a ![]() , illetve az
, illetve az ![]() háromszögek területei.
háromszögek területei.
Az ábra alapján nyilvánvaló az egyenlőtlenség helyessége.
A geometriai megoldásnak előnye itt is, hogy az ábráról könnyen leolvasható, mikor érhetők el, illetve hogyan közelíthetők a határok. Az alábbi ábrák mutatják, hogy az alsó határ akkor érhető el, ha ![]() , vagy
, vagy ![]() . A felső akkor, ha
. A felső akkor, ha ![]() ,
, ![]()
![]() közül egyik 0, a másik 1, a harmadik tetszőleges.
közül egyik 0, a másik 1, a harmadik tetszőleges.
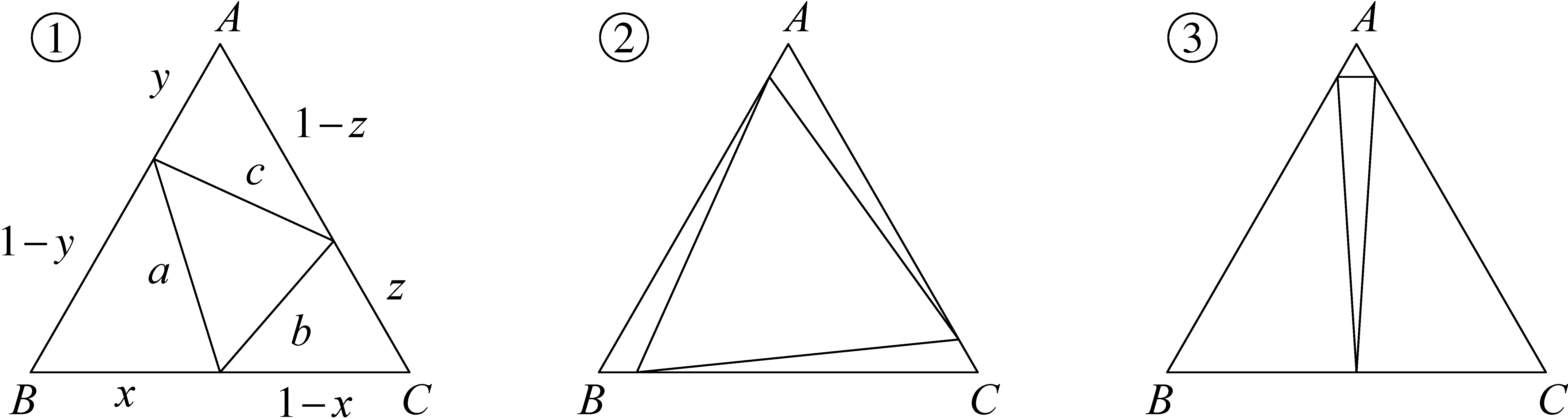
Megoldás nélkül adunk néhány algebra feladatot, amelyeket a geometriai, illetve trigonometriai megközelítéssel is megoldhatunk. További ilyen feladatokat találhatunk [2]-ben, illetve [3]-ban.
II/6. feladat. Igazoljuk, hogy
ha ![]() pozitív egész szám!
pozitív egész szám!
II/7. feladat. Igazoljuk, hogy ha ![]() ,
, ![]() ,
, ![]() pozitív számok, akkor
pozitív számok, akkor
II/8. feladat. Az ![]() ,
, ![]() ,
, ![]() feltételeknek megfelelő számnégyesek közül válasszuk ki azokat, amelyekre
feltételeknek megfelelő számnégyesek közül válasszuk ki azokat, amelyekre ![]() a legnagyobb!
a legnagyobb!
II/9. feladat. Mutassuk meg, hogy ha az ![]() ,
, ![]() ,
, ![]() ,
, ![]() valós számokra
valós számokra ![]() és
és ![]() , akkor
, akkor ![]() !
!
Nézzünk most egy másik megoldást a II/5. feladatra, és gondoljuk tovább, hogyan lehet még hatékonyabban használni az alkalmazott ötletet.
II/5. feladat 3. megoldása (függvénytani). Az ![]() kifejezést tekintsük
kifejezést tekintsük ![]() függvényének, ahol
függvényének, ahol ![]() és
és ![]() paraméterek.
paraméterek.
ahol ![]() .
.
Most is elegendő csak a jobb oldali egyenlőtlenséget vizsgálni. Egy korlátos, zárt intervallumon értelmezett lineáris függvény szélsőértékeit az intervallum valamelyik végpontjában veszi fel, ezért elegendő megmutatni, hogy ![]() , és
, és ![]() . (Ha a függvény konstans, akkor is a végpontokban veszi fel szélsőértékét, de nemcsak ott.)
. (Ha a függvény konstans, akkor is a végpontokban veszi fel szélsőértékét, de nemcsak ott.) ![]() ,
,
Ez igaz, mert az utolsó egyenlőtlenségben a feltételek szerint mindkét tényező nemnegatív.
![]() , a feltételek szerint ez is igaz.
, a feltételek szerint ez is igaz.
A felhasznált ötlet alkalmazható, ha olyan kifejezés maximumát keressük, amely valamelyik változónak lineáris függvénye, és ez a változó egy korlátos zárt intervallumon veszi fel értékeit. Ilyenkor elegendő a két végpontban felvett függvényértéket vizsgálni.
Mindkét feltétel a feladatok viszonylag szűk rétegében teljesül. A következő feladatban kissé szélesebb körben alkalmazzuk a fenti ötletet.
II/10. feladat. Igazoljuk, hogy ha ![]() ,
, ![]() ,
, ![]() , akkor:
, akkor:![]()
Megoldás. Tekintsük a ![]() intervallumon értelmezett
intervallumon értelmezett ![]() függvényt. Azt kell belátnunk, hogy a
függvényt. Azt kell belátnunk, hogy a ![]() intervallumon
intervallumon ![]() .
.
Ha ![]() , akkor
, akkor ![]() , lineáris függvény, a II/5. feladat harmadik megoldása szerint elegendő belátni, hogy
, lineáris függvény, a II/5. feladat harmadik megoldása szerint elegendő belátni, hogy ![]() és
és ![]() . Ez az adott intervallumon teljesül.
. Ez az adott intervallumon teljesül.
Ha ![]() , akkor
, akkor ![]() grafikonja egyenes állású parabola, ezért
grafikonja egyenes állású parabola, ezért ![]() a
a ![]() intervallum valamelyik végpontjában veszi fel maximumát.
intervallum valamelyik végpontjában veszi fel maximumát.
Mindkét esetben az első tényező nem negatív, a második nem pozitív, ezért szorzatuk nem pozitív.
Most a felhasznált függvények köre bővült, de az még mindig eléggé leszűkíti az alkalmazhatóság körét, hogy a változók egy korlátos zárt intervallumon veszik fel értékeit.
A következő feladatban egy még szélesebb függvényhalmazban alkalmazzuk ötletünket.
II/11. feladat. Az ![]() ,
, ![]() ,
, ![]() valós számokra teljesül, hogy
valós számokra teljesül, hogy ![]() . Mutassuk meg, hogy
. Mutassuk meg, hogy
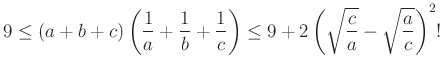
Megoldás. A bal oldali egyenlőtlenség közismert, azonnal következik például az ![]() ,
, ![]() ,
, ![]() pozitív számokra felírt harmonikus és számtani közepek között fennálló
pozitív számokra felírt harmonikus és számtani közepek között fennálló
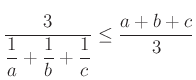
egyenlőtlenségből. Egyenlőség ![]() esetén teljesül.
esetén teljesül.
A jobb oldali egyenlőtlenség igazolásához tekintsük az ![]() intervallumon értelmezett
intervallumon értelmezett
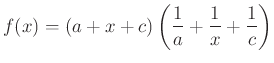
függvényt.
Azt kell belátnunk, hogy az ![]() intervallumon
intervallumon
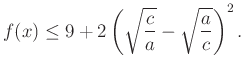
Az ![]() függvényt
függvényt
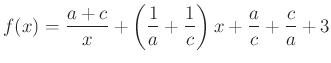
alakban írva látható, hogy a 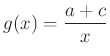 törtfüggvény és a
törtfüggvény és a 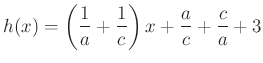 lineáris függvények összege, ezért a pozitív számok halmazán, így az
lineáris függvények összege, ezért a pozitív számok halmazán, így az ![]() intervallumon is folytonos és konvex.
intervallumon is folytonos és konvex.
Egy korlátos zárt intervallumon folytonos, konvex függvény az intervallum valamelyik végpontjában felveszi a maximumát.
Ezért elegendő belátnunk, hogy
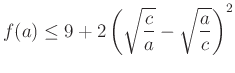 |
(*) |
és
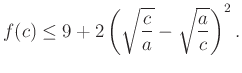 |
(**) |
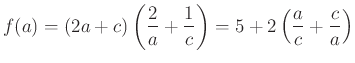
és
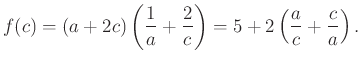
Továbbá
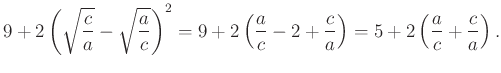
Ezért a (*) és (**) egyenlőtlenségek teljesülnek. Látható az is, hogy egyenlőség ![]() vagy
vagy ![]() esetén teljesül.
esetén teljesül.
Bevezetőnkben megvizsgálandó kérdésnek ajánlottuk, hogy szükség volt-e minden feltételre, felhasználtuk-e azt teljes egészében. Az utóbbi három feladat szép példa volt arra, hogy a feltételek továbbgondolásával hogyan lehet szélesebb körben használhatóvá tenni egy ötletet. (Azt, hogy elegendő az intervallum végpontjaiban felvett függvényértéket vizsgálni.) Az első feladatban lineáris függvényre alkalmaztuk, de ha csak a maximumát keressük a kifejezésnek, akkor „egyenes állású” másodfokú függvénynél is alkalmazható, a harmadikban pedig csak azt használtuk fel, hogy a függvény konvex. A következő feladatok megoldásához is ajánljuk a fenti ötlet alkalmazását.
II/12. feladat. Az ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() valós számok a
valós számok a ![]() intervallum elemei, ahol
intervallum elemei, ahol ![]() . Igazold, hogy
. Igazold, hogy
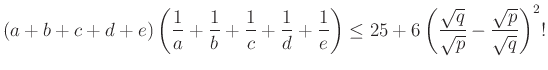
II/13. feladat. Az ![]() valós számok az
valós számok az ![]() intervallum elemei, ahol
intervallum elemei, ahol ![]() . Igazold, hogy
. Igazold, hogy
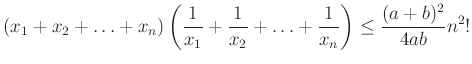
II/14. feladat. Legyenek ![]() és
és ![]() pozitív valós számok, és legyenek
pozitív valós számok, és legyenek ![]() (
( ![]() ) olyan valós számok, amelyekre
) olyan valós számok, amelyekre ![]() . Igazoljuk, hogy akkor
. Igazoljuk, hogy akkor
Katz Sándor
a Bonyhádi Petőfi Sándor Evangélikus Gimnázium
és az Erdős Pál Tehetséggondozó Iskola tanára
Irodalomjegyzék
- 1
- Katz Sándor: Matematika versenyfeladatok. A Fejér Lipót matematikaverseny feladatai 1987—2006. Zalai Matematikai Tehetségekért Alapítvány 2009.
- 2
- Róka Sándor: Algebrai feladatok megoldása geometriai hátérrel. A Matematika Tanítása 1996. 3. sz.
- 3
- Katz Sándor: Néhány algebra feladat megoldása trigonometriai módszerekkel. POLYGON 2003. 1—2 sz.
- 4
- K. A. Mnacakanyan, I. M. Szedrakjan: Egy függvénytulajdonság alkalmazása némely egyenlőtlenségekben MATEMATIKA V SKOLJE 1988/6. sz.
Lábjegyzetek
- 1
- Megjegyzés:
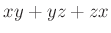 pontos értéke is kiszámítható. Szerk.
pontos értéke is kiszámítható. Szerk. - 2
- Ez a háromszög úgynevezett izogonális pontja. Nem minden háromszögben esik a háromszög belsejébe — mint látni fogjuk, ezt kihasználjuk —, csak amelyekben minden szög is kisebb
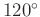 -nál. Az 5, 6, 7 oldalú háromszögben, mint az egyszerűen ellenőrizhető, ez a tulajdonság teljesül. Szerk.
-nál. Az 5, 6, 7 oldalú háromszögben, mint az egyszerűen ellenőrizhető, ez a tulajdonság teljesül. Szerk. - 3
- Ha lenne egy másik pozitív
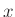 megoldás is, például
megoldás is, például 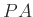 -nál kisebb, akkor az első egyenlet szerint ehhez nagyobb pozitív
-nál kisebb, akkor az első egyenlet szerint ehhez nagyobb pozitív 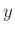 tartozna, de ehhez a második egyenlet szerint kisebb pozitív
tartozna, de ehhez a második egyenlet szerint kisebb pozitív 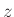 lenne, és így a harmadik egyenletben kisebb
lenne, és így a harmadik egyenletben kisebb 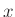 -ből és
-ből és 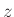 -ből nem kaphatnánk 49-et.
-ből nem kaphatnánk 49-et. - Ugyanebben a számunkban olvasható a Rátz László Vándorgyűlésről szóló beszámoló.