Információk

 Aktuális szám: 4. szám 2017. június 

Mi is... egy G2-sokaság?

Mi is... egy G2-sokaság?

A $ G_2$-sokaság olyan Riemann-sokaság, melynek holonómiacsoportját a kivételes $ G_2$ Lie-csoport tartalmazza. Ebben a cikkben megmagyarázzuk ezt a definíciót, leírjuk a $ G_2$-sokaságok néhány fontos tulajdonságát, és megvizsgáljuk, hogy milyen hasonlóságok és különbségek fedezhetők fel ezen terek és a Kähler-, valamint a Calabi—Yau-sokaságok között. 

Egy Riemann-sokaság holonómiacsoportja egy kompakt Lie-csoport, amely bizonyos értelemben globális mértékét adja a sokaság lokális görbületének. A sokaságra és a metrikára tett megfelelően szép feltételek mellett az öt kivételes Lie-csoport közül csak a $ G_2$ léphet fel a tér holonómiacsoportjaként. Berger 1950-es klasszifikációja ugyan nem zárta ki, de az volt az általános nézet, hogy ilyen metrikák nem léteznek. 1987-ben azonban Robert Bryant sikeresen bizonyította lokális példák létezését. Két évvel később — bizonyos vektornyalábok totális terén egy szimmetriamódszert alkalmazva — Bryant és Simon Salamon találta az első teljes, nem-kompakt példákat ilyen metrikákra. Azóta fizikusok igen sok további példát találtak szimmetriával rendelkező $ G_2$-holonómiájú nem kompakt terekre. Végül 1994-ben Dominic Joyce okozott nagy meglepetést több száz kompakt példa létezését bizonyítva. Bizonyítása nem konstruktív, felhasználja bizonyos nemlineáris elliptikus egyenletek megoldásának egzisztencia és unicitási eredményeit, ahogy a Kähler-sokaságokon a Calabi-sejtés Yau-féle megoldása sem konstruktív módon igazolja a bizonyos feltételeknek eleget tevő Calabi—Yau-típusú ($ SU(m)$-holonómiájú) metrikák egzisztenciáját és unicitását. 2000-ben Alekszej Kovaljov talált $ G_2$-holonómiájú kompakt sokaságokra egy másik konstrukciót, mellyel több száz újabb, nem explicit példát adott. Kompakt esetekre jelenleg is csak ez a két konstrukció ismert. A $ G_2$-geometriákról és néhány kompakt példáról kiváló áttekintést találunk a [3] monográfiában.

A Riemann-holonómiát illetően a $ G_2$ csoport jelentősége valójában nem abban rejlik, hogy ez egyike az öt kivételes Lie-csoportnak, hanem abban, hogy ez az automorfizmuscsoportja az októnionok $ \mathbb{O}$ nyolcdimenziós nem asszociatív valós divízióalgebrájának. Az októnionokon adott egy pozitív definit belső szorzat; továbbá az $ 1 \in \mathbb{O}$ egységelem által kifeszített alteret valós, míg az ortogonális komplementerét tisztán képzetes októnionoknak nevezzük: $ \mathrm{Im}(\mathbb{O})\cong \mathbb{R}^7$. Ez teljesen analóg a kvaterniók $ \mathbb{H}$ algebrájával, azzal a különbséggel, hogy az assszociativitás hiánya bizonyos bonyodalmakat okoz. Az analógia alapján bevezethetünk $ \mathbb{R}^7$-en egy keresztszorzást az alábbi módon: legyen $ u,v\in \mathbb{R}^7\cong \mathbb{O}$, és legyen $ u\times v=\mathrm{Im}(uv)$, ahol $ uv$ az októnionok szorzatát jelöli. (Az $ uv$ szorzat valós része nem más, mint $ -\langle u,v\rangle$, pontosan úgy, ahogy a kvaterniók esetén, ahol $ \langle \cdot, \cdot \rangle$ az euklideszi belső szorzást jelöli.) Az így bevezetett keresztszorzat eleget tesz az 

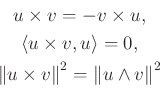
\begin{displaymath}\begin{gathered}u\times v=-v\times u,\\ \langle u\times v, u\... ...ight\rVert^2=\left\lVert u\wedge v\right\rVert^2 \end{gathered}\end{displaymath}

relációknak, pontosan úgy, ahogy az $ \mathbb{R}^3\cong \mathrm{Im}(\mathbb{H})$-n bevezetett keresztszorzat teszi. Ugyanakkor van egy különbség: az $ \mathbb{R}^3$ keresztszorzatával ellentétben

$\displaystyle u\times(v\times w)+\langle u,v\rangle w-\langle u,w\rangle v $

nem zérus, hanem a szorzat nemasszociativitását méri: $ (uv)w-u(vw)\neq 0$. Megjegyezzük, hogy $ \mathbb{R}^7$-ben a keresztszorzást felhasználva bevezethetünk egy 3-formát (mindhárom változójában lineáris és antiszimmetrikus formát) az alábbi módon: $ \varphi(u,v,w)=\langle u \times v, w\rangle$. Itt nem részletezett okok miatt ezt a formát asszociatív 3-formának nevezzük.

Azt mondjuk, hogy egy 7-dimenziós sokaságon megadható egy $ G_2$-struktúra, ha megadható a hozzá tartozó frame-nyaláb $ GL(7, \mathbb{R})$ struktúracsoportjának egy redukciója a természetes módon $ SO(7)$-beli részcsoportnak tekinthető $ G_2$ csoportra. Ebből következik, hogy egy $ G_2$-struktúra meghatároz egy Riemann-metrikát és egy irányítást. Valóban, egy $ G_2$-struktúrával ellátott sokaságon létezik egy „nemelfajuló” $ \varphi$ 3-forma, melyre igaz, hogy az $ M$ sokaság minden $ p$ pontja körül megadható olyan koordinátarendszer, hogy a $ p$ pontban a $ \varphi$ megegyezik az $ \mathbb{R}^7$-en korábban bevezetett asszociatív 3-formával. Továbbá a $ \varphi$ 3-formából egy metrika és egy irányítás származtatható kanonikus, ugyanakkor erősen nemlineáris módon. E metrika segítségével a $ \varphi$-ből az „indexek felemelésével” bevezethetünk egy keresztszorzatot. Összegezve: a $ G_2$-struktúrával rendelkező $ (M, \varphi)$ sokaság ellátható metrikával, keresztszorzással, 3-formával és irányítással, melyek eleget tesznek a

$\displaystyle \varphi(u,v,w)=\langle u\times v,w\rangle $

feltételnek. Ez teljesen hasonló a majdnem Hermite-sokaságok megfelelő struktúrájához, ahol adva van egy metrika, egy $ J$ majdnem komplex struktúra, egy $ \omega$ 2-forma és egy irányítás, melyek eleget tesznek az

$\displaystyle \omega(u,v)=\langle Ju,v\rangle $

feltételnek. Lényegében egy sokaságon akkor adható meg egy $ G_2$-struktúra, ha az érintőtere sima módon azonosítható a képzetes októnionok $ \mathrm{Im}(\mathbb{O})\cong \mathbb{R}^7$ terével, ahogy egy Hermite-sokaság esetén is az érintőtér sima módon azonosítható (a szokásos euklideszi belső szorzattal ellátott) $ \mathbb{C}^m$-mel. Az Hermite-sokaságok pszeudo-holomorf görbéihez hasonlóan a $ G_2$-struktúrával rendelkező sokaságokon is megadhatók kalibrált részsokaságok kitüntetett osztályai. A kalibrált részsokaságokról bővebben a [2] dolgozatban olvashatunk.

Annak szükséges és elégséges feltétele, hogy egy sokaságon létezzen $ G_2$-struktúra, az, hogy irányítható és hogy spin legyen, ami ekvivalens azzal, hogy az első két Stiefel—Whitney-osztálya zérus. Így tehát igen sok ilyen 7-dimenziós sokaság van, ahogy igen sok majdnem Hermite-sokaság is van. De a történetnek itt még nincs vége.

Legyen $ (M, \varphi)$ egy $ G_2$-struktúrával rendelkező sokaság. Mivel ez meghatároz egy $ g_\varphi$ Riemann-metrikát és egy ehhez tartozó $ \nabla$ Levi-Civita-féle kovariáns deriválást is, vizsgálhatjuk, hogy teljesül-e a $ \nabla\varphi=0$ feltétel. Ha igen, akkor az $ (M, \varphi)$-t $ G_2$-sokaságnak nevezzük, és ekkor megmutatható, hogy a $ g_\varphi$ Riemann-féle holonómiacsoportját tartalmazza a $ G_2\subset SO(7)$ csoport. Egy ilyen „párhuzamos” $ G_2$-struktúrát találni igen nehéz, mert az ismeretlen $ \varphi$ 3-formára egy bonyolult nemlineáris parciális differenciálegyenletet kell megoldani. A $ G_2$-sokaságok esete bizonyos értelemben hasonló a Kähler-sokaságokéhoz, melyek pontosan azok a majdnem Hermite-sokaságok, melyekre teljesül a $ \nabla \omega=0$ feltétel. Ugyanakkor Kähler-sokaságokat sokkal könnyebb találni részben azért, mert a $ g$ metrika és a $ J$ komplex struktúra lényegében függetlenek egymástól (csak egy enyhe kompatibilitási feltételnek kell eleget tenniük), míg a $ G_2$-sokaságok esetén mind a metrika, mind a keresztszorzat nemlineárisan származtatható a metrikából. Azonban az analógia nem teljes, mert megmutatható, hogy ha $ \nabla\varphi=0$, akkor a $ g_\varphi$ Ricci-görbülete eltűnik. Így tehát egy $ G_2$-sokaság mindig Ricci-lapos. (Ez az egyik magyarázata annak, hogy miért érdeklik a fizikusokat ezek a sokaságok: a 11-dimenziós $ M$-elméletben — csakúgy, ahogy a Calabi—Yau-féle 3-sokaságok a 10-dimenziós húrelméletben — a „kompaktifikáció” szerepét játsszák. Az [1] dolgozatban áttekintést találunk a $ G_2$-sokaságok szerepéről a fizikában.) Tehát bizonyos értelemben a $ G_2$-sokaságok hasonlóak az olyan Ricci-lapos Kähler-sokaságokhoz, melyek épp a Calabi—Yau-sokaságok.

Ha megengedjük, hogy a holonómia valódi részcsoportja legyen a $ G_2$ csoportnak, akkor igen sok példát kaphatunk $ G_2$-sokaságra. Például a lapos $ T^7$ tórusznak, vagy a $ T^3\times CY2$ és az $ S^1\times CY3$ szorzatsokaságoknak is (ahol $ CYn$ egy Calabi—Yau-féle $ n$-sokaságot jelöl) a holonómiacsoportja a $ G_2$-nek egy-egy valódi részcsoportja. Bizonyos értelemben ezek „triviális” példák, mert alacsonyabb dimenziós konstrukciókra redukálódnak. Az olyan sokaságokat, melyek holonómiacsoportja a teljes $ G_2$ csoport, irreducibilis $ G_2$-sokaságoknak nevezzük. Éppen ilyenek azok a sokaságok, melyeket Bryant, Bryant—Salamon, Joyce és Kovaljov konstruált.

Még hiányzik egy „Calabi—Yau-típusú” tétel, mely megadná annak szükséges és elégséges feltételét, hogy egy kompakt 7-dimenziós sokaságon, melyen megadható $ G_2$-struktúra, mikor adható meg olyan $ G_2$-struktúra, mely párhuzamos ( $ \nabla\varphi=0$). Igazából még azt sem tudjuk, hogy mi lenne az erre vonatkozó sejtés. Néhány topologikus feltétel már ismert, de messze vagyunk még attól, hogy elegendőségi feltételt adjunk. De ahelyett, hogy ezt a problémát a Calabi-sejtéshez hasonlítanánk, inkább egy másikkal kellene összevetni, amelyre jobban hasonlít. Nevezetesen a következőhöz: tegyük fel, hogy $ M$ egy $ 2n$-dimenziós kompakt, sima sokaság, melyen megadható egy majdnem komplex struktúra. Mi annak a szükséges és elégséges feltétele, hogy az $ M$-en létezzen Kähler-metrika? Számos szükséges topologikus feltétel ugyan ismert, de közelében sem vagyunk annak, hogy elegendőségi feltételt adjunk.

Ami miatt a Calabi-sejtés mégis kezelhető (bár kétségkívül nehéz), az az a tény, hogy ha egy Kähler-sokaságból indulunk ki (ahol a metrika holonómiája $ U(m)$), akkor az $ SU(m)$-hez csak eggyel kell csökkenteni a holonómiacsoport dimenzióját. Ezután a Kähler-geometria $ \partial \overline{\partial}$-lemmája alapján a Calabi-sejtést egy skalárfüggvényre vonatkozó (bár erősen nem lineáris) elliptikus parciális differenciálegyenlet megoldhatóságára lehet visszavezetni. Hasonló „sejtés” a Kähler- vagy a $ G_2$-sokaságok esetén parciális differenciálegyenlet-rendszerek megoldhatóságára vezet, melyeket sokkal nehezebb kezelni. 

Spiro Karigiannis

Irodalomjegyzék

[1] S. Gukov, M-theory on manifolds with exceptional holonomy, Fortschr. Phys. 51 (2003), 719—731. 

[2] R. Harvey and H. B. Lawson, Calibrated geometries, Acta Math. 148 (1982), 47—157. 

[3] D. Joyce, Compact Manifolds with Special Holonomy, Oxford University Press, 2000.

Megjegyzések

  • Spiro Karigiannis a University of Waterloo adjunktusa. E-mail címe: Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.
  • A cikk egy korábbi változata a MathOverflow-ban feltett kérdésre adott válaszként jelent meg, és elérhető a http://mathoverflow.net/questions/49357/g-2-and-geometry címen.
  • A szerző köszönetet mond Pete L. Clarknak, aki e cikket a Notices of the AMS folyóirat “WHAT IS ...?” rovatába javasolta.

 

  • A fenti dolgozat eredetije 2011 áprilisában jelent meg a Notices of the American Mathematical Society folyóiratban. Ez a fordítás a szerző és az AMS engedélyével  jelenik meg.   Fordította Muzsnay Zoltán. 
  • Spiro Karigiannis, WHAT IS...a G2-Manifold? Notices Amer. MAth. Soc. Vol. 58 Num. 4 (April, 2011) 580-581 ©2011 American Mathematical Society.