A csáp (angolul grope, ami „tapogatózást” jelent) egy matematikai kifejezés, amely nyomtatásban először Jim Cannon 1978-as Bulletinben közölt cikkében [1] jelent meg. Ő a kifejezés kitalálójának egy madisoni geometriai topológus kollégáját, Russ McMillant tartotta. Cannon elmagyarázta, hogy azért nevezték ezt a dolgot csápnak, mert „számos tapogatózó ujj nő ki belőle”. Arra is felhívta a figyelmet, hogy „ez a szóhasználat rossz szóviccekhez vezethet” – némelyiknek ő sem tudott ellenállni. Az évek során még publikálásra szánt cikkek is vissza lettek utasítva, mert használták a csáp szót.
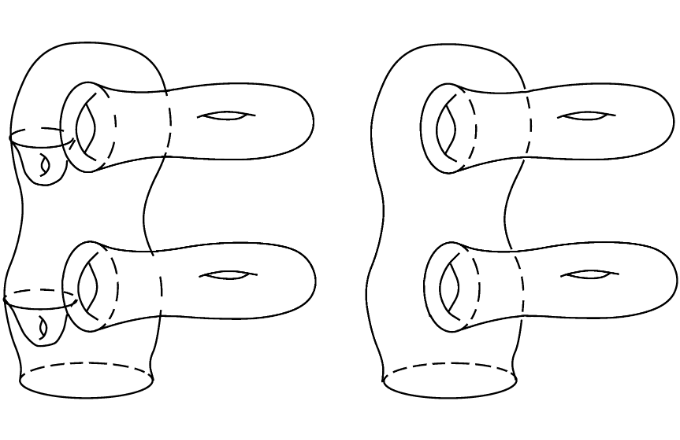
2 magasságú (balra) és 3 osztályú (jobbra) csápok
Matematikailag egy csáp egy bizonyos ![]() -dimenziós komplexus (amelynek egy körvonal a határa), amely felületek uniója (ahol felületen egy kompakt, összefüggő, irányított
-dimenziós komplexus (amelynek egy körvonal a határa), amely felületek uniója (ahol felületen egy kompakt, összefüggő, irányított ![]() -dimenziós sokaságot értünk egy határoló körvonallal). Ahhoz, hogy beszélhessünk arról, hogyan vannak ezek a felületek összeragasztva, egy komplexitást mérő fogalmat, a csáp magasságát vezetjük be. Ha a csáp
-dimenziós sokaságot értünk egy határoló körvonallal). Ahhoz, hogy beszélhessünk arról, hogyan vannak ezek a felületek összeragasztva, egy komplexitást mérő fogalmat, a csáp magasságát vezetjük be. Ha a csáp ![]() magassága
magassága ![]() , akkor a csáp csak egy
, akkor a csáp csak egy ![]() felület. Ha
felület. Ha ![]() , ahol
, ahol ![]() a
a ![]() felület génusza, akkor alkossák az
felület génusza, akkor alkossák az ![]() -k a
-k a ![]() felület egy körökből álló teljes szimplektikus bázisát. Ekkor egy
felület egy körökből álló teljes szimplektikus bázisát. Ekkor egy ![]() magasságú csápot úgy kapunk, hogy
magasságú csápot úgy kapunk, hogy ![]() magasságú csápokat ragasztunk az
magasságú csápokat ragasztunk az ![]() -khez a csápok határoló körei mentén.
-khez a csápok határoló körei mentén.
Ezért a csápok nem sokaságok, de az előforduló szingularitásaik nagyon egyszerű típusúak, úgyhogy ezek a ![]() -komplexusok bizonyos értelemben a felületek után a legegyszerűbb terek. Hogy motiváljuk a csápok és magasságuk definíciójának bevezetését, a következőkben elmagyarázzuk, hogyan kapcsolódik mindez a csoportelmélethez.
-komplexusok bizonyos értelemben a felületek után a legegyszerűbb terek. Hogy motiváljuk a csápok és magasságuk definíciójának bevezetését, a következőkben elmagyarázzuk, hogyan kapcsolódik mindez a csoportelmélethez.
Csoport kommutátorok és csápok
Egy ![]() (a körvonalból valamilyen
(a körvonalból valamilyen ![]() térbe menő) folytonos leképezés a
térbe menő) folytonos leképezés a ![]() fundamentális csoportnak egy elemét reprezentálja. Ez a leképezés pontosan akkor terjed ki valamilyen felületnek (azaz egy 1 magasságú csápnak) az
fundamentális csoportnak egy elemét reprezentálja. Ez a leképezés pontosan akkor terjed ki valamilyen felületnek (azaz egy 1 magasságú csápnak) az ![]() -be menő leképezésévé, ha egy kommutátort reprezentál
-be menő leképezésévé, ha egy kommutátort reprezentál ![]() -ben. Ezt úgy láthatjuk a legkönnyebben, hogy a
-ben. Ezt úgy láthatjuk a legkönnyebben, hogy a ![]() génuszú
génuszú ![]() felületre mint párosított oldalakkal rendelkező (és középen kilyukasztott)
felületre mint párosított oldalakkal rendelkező (és középen kilyukasztott) ![]() -szögre gondolunk. Ezt a párosítást úgy kapjuk, hogy vesszük a következő szót a
-szögre gondolunk. Ezt a párosítást úgy kapjuk, hogy vesszük a következő szót a ![]() -szög határának mentén:
-szög határának mentén:
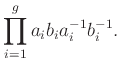
Mivel ![]() határoló köre a
határoló köre a ![]() -szög közepén helyezkedik el, ezzel a kommutátorral kell megegyeznie. Iterált kommutátorok hasonlóan fejezhetők ki csápok
-szög közepén helyezkedik el, ezzel a kommutátorral kell megegyeznie. Iterált kommutátorok hasonlóan fejezhetők ki csápok ![]() -be menő folytonos leképezéseivel: egy
-be menő folytonos leképezéseivel: egy ![]() leképezés pontosan akkor reprezentálja
leképezés pontosan akkor reprezentálja ![]() leszálló lánca
leszálló lánca ![]() -adik tagjának egy elemét, ha kiterjed egy
-adik tagjának egy elemét, ha kiterjed egy ![]() magasságú csáp folytonos leképezésévé. Emlékeztetünk rá, hogy egy
magasságú csáp folytonos leképezésévé. Emlékeztetünk rá, hogy egy ![]() csoport leszálló lánca a
csoport leszálló lánca a ![]() iterált kommutátorokkal van definiálva. A csoport feloldható, ha ez a sorozat
iterált kommutátorokkal van definiálva. A csoport feloldható, ha ez a sorozat ![]() -ben végződik. A leszálló láncnak egy közeli rokona az alsó centrális lánc, melyet a
-ben végződik. A leszálló láncnak egy közeli rokona az alsó centrális lánc, melyet a ![]() csoportra a
csoportra a ![]() definícióval adunk meg. A csoport nilpotens, ha ez a sorozat
definícióval adunk meg. A csoport nilpotens, ha ez a sorozat ![]() -ben végződik. Az olvasó megpróbálhatja elképzelni hogyan definiáljunk bizonyos
-ben végződik. Az olvasó megpróbálhatja elképzelni hogyan definiáljunk bizonyos ![]() -komplexusokat (egy határoló körvonallal), amelyeket
-komplexusokat (egy határoló körvonallal), amelyeket ![]() osztályú csápoknak hívunk, úgy, hogy egy
osztályú csápoknak hívunk, úgy, hogy egy ![]() leképezés pontosan akkor reprezentáljon egy elemet
leképezés pontosan akkor reprezentáljon egy elemet ![]() alsó centrális láncának
alsó centrális láncának ![]() -edik tagjában, ha kiterjed egy
-edik tagjában, ha kiterjed egy ![]() osztályú csáp folytonos leképezésévé. Valójában az ilyen csápok általánosabbak, mint amelyeket legelőször definiáltunk, és a szóhasználat meg is változott az évek során: a
osztályú csáp folytonos leképezésévé. Valójában az ilyen csápok általánosabbak, mint amelyeket legelőször definiáltunk, és a szóhasználat meg is változott az évek során: a ![]() magasságú csápokat ma szimmetrikus csápoknak is nevezzük. Ezek a csoportelmélet szerint
magasságú csápokat ma szimmetrikus csápoknak is nevezzük. Ezek a csoportelmélet szerint ![]() osztályúak. Nem minden csáp szimmetrikus, ahogy azt a fenti ábra is mutatja.
osztályúak. Nem minden csáp szimmetrikus, ahogy azt a fenti ábra is mutatja.
Geometriai csoport kommutátorok
Ahogyan csápok leképezéseivel leírhatunk iterált kommutátorokat ![]() -ben, nézhetünk beágyazott csápokat is ahhoz, hogy több geometriai kérdést tanulmányozzunk. Ezeknek a legközvetlenebb felhasználása tűnik a legaktuálisabbnak, és ezt a csomóelmélet témakörében találjuk. A csomóelmélet a
-ben, nézhetünk beágyazott csápokat is ahhoz, hogy több geometriai kérdést tanulmányozzunk. Ezeknek a legközvetlenebb felhasználása tűnik a legaktuálisabbnak, és ezt a csomóelmélet témakörében találjuk. A csomóelmélet a ![]() -dimenziós térbe beágyazott körök elmélete (ami más, mint a körök folytonos leképezéseié a fundamentális csoport esetében). Emlékeztetünk rá, hogy minden csomó határol egy Seifert felületet a
-dimenziós térbe beágyazott körök elmélete (ami más, mint a körök folytonos leképezéseié a fundamentális csoport esetében). Emlékeztetünk rá, hogy minden csomó határol egy Seifert felületet a ![]() -dimenziós térben, de csak a triviális csomó határol beágyazott körlapot. Ezért az egész csomóelmélet a felületek és a körlap közötti különbségből ered. Ahogy láttuk, ez pont olyan, mint a különbség egy
-dimenziós térben, de csak a triviális csomó határol beágyazott körlapot. Ezért az egész csomóelmélet a felületek és a körlap közötti különbségből ered. Ahogy láttuk, ez pont olyan, mint a különbség egy ![]() -beli kommutátor és a csoportbeli egységelem között. A csápok lehetőséget adnak arra, hogy filtráljuk ezt a különbséget, hasonlóan a csoportelméletbeli iterált kommutátorokhoz.
-beli kommutátor és a csoportbeli egységelem között. A csápok lehetőséget adnak arra, hogy filtráljuk ezt a különbséget, hasonlóan a csoportelméletbeli iterált kommutátorokhoz.
![]() -dimenzióban gondolkodva oda jutunk, hogy
-dimenzióban gondolkodva oda jutunk, hogy ![]() -ben tanulmányozzuk a csomókat, amik kiterjednek
-ben tanulmányozzuk a csomókat, amik kiterjednek ![]() magasságú szimmetrikus csápok
magasságú szimmetrikus csápok ![]() -be való beágyazásaivá. Ez a csomó konkordizmuscsoport egy filtrálását adja meg, melyet Cochran, Orr és Teichner vezettek be 1998-ban. Megmutatták, hogy az összes előzőleg ismert konkordizmus invariáns megkapható ebből kis
-be való beágyazásaivá. Ez a csomó konkordizmuscsoport egy filtrálását adja meg, melyet Cochran, Orr és Teichner vezettek be 1998-ban. Megmutatták, hogy az összes előzőleg ismert konkordizmus invariáns megkapható ebből kis ![]() -ra. Például ha a csomó egy
-ra. Például ha a csomó egy ![]() magasságú szimmetrikus csápot határol
magasságú szimmetrikus csápot határol ![]() -ben, akkor az összes Casson-Gordon-invariánsa eltűnik. A csomó komplementumának feloldható fedéseivel és annak von Neumann-szignatúráival megmutatták továbbá, hogy ennek a filtrációnak minden egymás után következő faktora nemtriviális.
-ben, akkor az összes Casson-Gordon-invariánsa eltűnik. A csomó komplementumának feloldható fedéseivel és annak von Neumann-szignatúráival megmutatták továbbá, hogy ennek a filtrációnak minden egymás után következő faktora nemtriviális.
Schneiderman bebizonyította, hogy minden csomó, amelynek triviális az Arf-invariánsa, határol valamilyen tetszőlegesen nagy osztályú (nemszimmetrikus) csápot ![]() -ben. Viszont ha ilyen csápot a
-ben. Viszont ha ilyen csápot a ![]() -dimenziós térbe ágyazva keresünk, akkor egy gazdag obstrukcióelméletet kapunk. Ezt Conant és Teichner dolgozta ki, és szorosan kapcsolódik a Vassiliev-féle csomóinvariánsokhoz, ahol a csáp osztálya pontosan megfelel az invariáns véges típusának.
-dimenziós térbe ágyazva keresünk, akkor egy gazdag obstrukcióelméletet kapunk. Ezt Conant és Teichner dolgozta ki, és szorosan kapcsolódik a Vassiliev-féle csomóinvariánsokhoz, ahol a csáp osztálya pontosan megfelel az invariáns véges típusának.
A csápok ezen ![]() - és
- és ![]() -dimenziós alkalmazásainak áttekintéséhez és további hivatkozásokhoz [3]-at ajánljuk.
-dimenziós alkalmazásainak áttekintéséhez és további hivatkozásokhoz [3]-at ajánljuk.
A csápok rövid története
Csápokhoz hasonló objektumok először 1971-ben tűntek fel Stanko egy cikkében, aki megmutatta, hogy bizonyos ![]() kodimenziós vad beágyazások sima beágyazásokat közelítenek meg. 1975-ben Cannon és Ancel kiterjesztették Stanko technikáját
kodimenziós vad beágyazások sima beágyazásokat közelítenek meg. 1975-ben Cannon és Ancel kiterjesztették Stanko technikáját ![]() kodimenzióra. 1977-ben Cannon bevezette a csápokat és a diszjunkt körlap tulajdonságot, hogy bebizonyítson számos sokaság-felismerési tételt. Közöttük volt a híres Kétszeres szuszpenzió tétel, ami azt állítja, hogy egy tetszőleges
kodimenzióra. 1977-ben Cannon bevezette a csápokat és a diszjunkt körlap tulajdonságot, hogy bebizonyítson számos sokaság-felismerési tételt. Közöttük volt a híres Kétszeres szuszpenzió tétel, ami azt állítja, hogy egy tetszőleges ![]() -dimenziós homologikus gömb kétszeres szuszpenziója homeomorf a standard
-dimenziós homologikus gömb kétszeres szuszpenziója homeomorf a standard ![]() -dimenziós gömbbel. (Egy
-dimenziós gömbbel. (Egy ![]() tér szuszpenziója az
tér szuszpenziója az ![]() két kúpjának
két kúpjának ![]() mentén vett uniója.) Az eredmény rendkívül meglepő volt, mivel egy
mentén vett uniója.) Az eredmény rendkívül meglepő volt, mivel egy ![]() sokaság egyszeri szuszpenziója csak akkor lehet sokaság, ha
sokaság egyszeri szuszpenziója csak akkor lehet sokaság, ha ![]() a standard gömb. Cannon előtt, és csápok használata nélkül Bob Edwards sok egyedi esetben bebizonyította a kétszeres szuszpenzió tételt (és belátta a Háromszoros szuszpenzió tételt). De ezen problémák megoldásában a csápok olyan sikeresnek bizonyultak, hogy Edwards azt javasolta,
a standard gömb. Cannon előtt, és csápok használata nélkül Bob Edwards sok egyedi esetben bebizonyította a kétszeres szuszpenzió tételt (és belátta a Háromszoros szuszpenzió tételt). De ezen problémák megoldásában a csápok olyan sikeresnek bizonyultak, hogy Edwards azt javasolta, ![]() -dimenziós topológiában is használják őket. Michael Freedman vezette be őket az 1983-as varsói Nemzetközi Matematikai Kongresszus kiadványában megjelent cikkében. Ebben a cikkben kiterjesztette a Körlap beágyazási tételét az egyszeresen összefüggő esetről jó fundamentális csoporttal rendelkező
-dimenziós topológiában is használják őket. Michael Freedman vezette be őket az 1983-as varsói Nemzetközi Matematikai Kongresszus kiadványában megjelent cikkében. Ebben a cikkben kiterjesztette a Körlap beágyazási tételét az egyszeresen összefüggő esetről jó fundamentális csoporttal rendelkező ![]() -sokaságokra. Ez magában foglalta a véges és ciklikus csoportokat (de még mindig nyitott kérdés, hogy mely csoportok jók, pillanatnyilag a szubexponenciális növekedésű csoportok a legáltalánosabb ismert osztály). A [2] monográfiában a
-sokaságokra. Ez magában foglalta a véges és ciklikus csoportokat (de még mindig nyitott kérdés, hogy mely csoportok jók, pillanatnyilag a szubexponenciális növekedésű csoportok a legáltalánosabb ismert osztály). A [2] monográfiában a ![]() -sokaságok topologikus elmélete teljes egészében a szimmetrikus csápokkal lett megfogalmazva.
-sokaságok topologikus elmélete teljes egészében a szimmetrikus csápokkal lett megfogalmazva.
Érdekes megfigyelni, hogyan tolódott a csápok felhasználása az évek során egyre alacsonyabb dimenziókba. A szlogen azonban mindig ugyanaz maradt: ha egy körlapot keresel, próbálj meg először egy csápot találni.
Peter Teichner
Irodalomjegyzék
- 1
- J. Cannon, The recognition problem: What is a topological manifold? Bull. Amer. Math. Soc. 84 (1978), 832-866.
- 2
- M. Freedman és F. Quinn, The topology of
 -manifolds, Princeton Math. Series 39, Princeton, NJ, 1990.
-manifolds, Princeton Math. Series 39, Princeton, NJ, 1990. - 3
- P. Teichner, Knots, von Neumann Signatures, and grope cobordism, Proceedings of the international congress of mathematicians, Vol H: Invited lectures, 2002, 437-446.
Megjegyzések
- Peter Teichner a Berkeley California Egyetem matematika professzora. E-mail címe: Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.
- A szerző köszönetet mond Ric Ancelnek a vizsgált fogalom eredetének tisztázásáért.
- A fenti dolgozat eredetije 2004 szeptemberében jelent meg a Notices of the American Mathematical Society folyóiratban. Peter Teichner, WHAT IS...a Grope? Notices Amer. Math. Soc. Vol. 51 Num. 8 (September, 2004) 894-895. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. Fordította Kalmár Boldizsár.









