Az alábbi cikk a Rényi Intézetben 2016 decemberében tartott összintézeti előadásom írásos változata. Előadásom célja az volt, hogy Sir Andrew Wiles Abel-díjának apropóján megismertessem a szélesebb matematikusközönséget azokkal a modern módszerekkel, amelyek a Fermat-sejtés megközelítésében kiemelt szerepet játszanak. Idő híján nem térhettem ki a Fermat-sejtés vizsgálata során elért híres történeti eredményekre, ezek bemutatása külön cikket kívánna. A módszerek igen haladott volta pedig sajnos nem tette lehetővé a téma elemi tárgyalását, ezért olvasóimról feltételeznem kell, hogy ismerik az absztrakt algebra, a számelmélet és a komplex függvénytan alapjait.
1. Faltings tételének alkalmazása
Mint az jól ismert, a Fermat-sejtés azt állítja, hogy ha ![]() egész szám, akkor az
egész szám, akkor az
egyenletnek nincs megoldása a pozitív egész számok körében. Ezzel ekvivalens, hogy az egész számok körében csak olyan megoldás van, ahol valamelyik változó 0 (és akkor persze a másik két változó legfeljebb csak egy előjelben különbözhet) — ezek a triviális megoldások.

A probléma ideális megközelítése az lenne, ha nemcsak a fenti speciális típusú egyenletekről, hanem egyenletek minél szélesebb családjáról ki tudnánk mutatni, hogy nincs pozitív egész megoldása. A legnevezetesebb általános állítás, amely a Fermat-egyenletre alkalmazható, a Mordell-sejtés, amelyet Gerd Faltings bizonyított 1983-ban. Faltings e Fields-érmes eredményének némileg szűkített verzióját a következőképpen fogalmazhatjuk meg. Bármely ![]() -edfokú 3-változós
-edfokú 3-változós ![]() homogén polinom nullhelyei egy síkgörbét határoznak meg a projektív síkban. E síkgörbe sima, ha a
homogén polinom nullhelyei egy síkgörbét határoznak meg a projektív síkban. E síkgörbe sima, ha a ![]() ,
, ![]() és
és ![]() parciális deriváltaknak nincs közös nullhelye az
parciális deriváltaknak nincs közös nullhelye az ![]() görbén.
görbén.
Faltings tétele. Legyen ![]() háromváltozós racionális együtthatós homogén polinom, amelynek foka legalább 4. Amennyiben az
háromváltozós racionális együtthatós homogén polinom, amelynek foka legalább 4. Amennyiben az ![]() síkgörbe sima, akkor csak véges sok egész koordinátájú pontja van a projektív síkban.
síkgörbe sima, akkor csak véges sok egész koordinátájú pontja van a projektív síkban.
Fontos itt emlékeznünk rá, hogy bármely ![]() szorzóra a
szorzóra a ![]() számhármasok a projektív síknak ugyanazt a pontját definiálják. Így például az
számhármasok a projektív síknak ugyanazt a pontját definiálják. Így például az ![]() számhármasok, amelyek a Fermat-egyenletnek minden
számhármasok, amelyek a Fermat-egyenletnek minden ![]() -ra triviális megoldásait adják, csak egyetlen pontot adnak a projektív síkban.
-ra triviális megoldásait adják, csak egyetlen pontot adnak a projektív síkban.
Faltings tétele tehát speciálisan a Fermat-egyenletről is azt állítja, hogy ![]() esetén konstans szorzótól eltekintve csak véges sok egész megoldása van. (Az
esetén konstans szorzótól eltekintve csak véges sok egész megoldása van. (Az ![]() esetet Euler már a 18. században megoldotta.) Másképp fogalmazva: ha az
esetet Euler már a 18. században megoldotta.) Másképp fogalmazva: ha az ![]() megoldások relatív prímek, az
megoldások relatív prímek, az ![]() abszolút érték valamely véges
abszolút érték valamely véges ![]() korlát alatt marad. Amennyiben
korlát alatt marad. Amennyiben ![]() -re tudnánk valamilyen kiszámítható alakot (ezt nevezik a Mordell-sejtés effektív változatának), akkor lehetséges volna a Fermat-sejtést adott
-re tudnánk valamilyen kiszámítható alakot (ezt nevezik a Mordell-sejtés effektív változatának), akkor lehetséges volna a Fermat-sejtést adott ![]() -re úgy igazolni, hogy a
-re úgy igazolni, hogy a ![]() korlátig elmenve ellenőrizzük, hogy nincs nemtriviális megoldás, majd alkalmazzuk a tételt. Sajnos azonban Faltings eredménye csak a
korlátig elmenve ellenőrizzük, hogy nincs nemtriviális megoldás, majd alkalmazzuk a tételt. Sajnos azonban Faltings eredménye csak a ![]() konstans létezését igazolja.
konstans létezését igazolja.
Mégis, egy egyszerű ötlettel levezethető Faltings tételéből, hogy a Fermat-sejtés „majdem minden” ![]() -re igaz. Michael Filaseta találta az alábbi trükköt. Fixáljunk egy
-re igaz. Michael Filaseta találta az alábbi trükköt. Fixáljunk egy ![]() pozitív egészt. Ekkor a fentiek szerint a
pozitív egészt. Ekkor a fentiek szerint a ![]() -edfokú Fermat-egyenlet relatív prím megoldásainak szorzata legfeljebb
-edfokú Fermat-egyenlet relatív prím megoldásainak szorzata legfeljebb ![]() abszolút értékű. Ha most
abszolút értékű. Ha most ![]() egész, akkor az
egész, akkor az ![]() fokú Fermat-egyenlet minden
fokú Fermat-egyenlet minden ![]() pozitív egész megoldására
pozitív egész megoldására ![]() megoldása a
megoldása a ![]() -edfokú Fermat-egyenletnek, tehát ha még
-edfokú Fermat-egyenletnek, tehát ha még ![]() relatív prímek is, akkor
relatív prímek is, akkor ![]() . Mivel itt
. Mivel itt ![]() , nyilvánvalóan
, nyilvánvalóan ![]() . Vagyis a Fermat-sejtés igaz minden olyan
. Vagyis a Fermat-sejtés igaz minden olyan ![]() kitevőre, amely osztható
kitevőre, amely osztható ![]() -vel. Ha most
-vel. Ha most ![]() -t változtatjuk, akkor ilyen
-t változtatjuk, akkor ilyen ![]() nagyon sok van. Pontosabban egy rövid szitamódszeres leszámlálással Andrew Granville és Roger Heath-Brown egymástól függetlenül a következőt vezették le Filaseta észrevételéből:
nagyon sok van. Pontosabban egy rövid szitamódszeres leszámlálással Andrew Granville és Roger Heath-Brown egymástól függetlenül a következőt vezették le Filaseta észrevételéből:
Tétel. Adott ![]() -ra jelölje
-ra jelölje ![]() azon
azon ![]() kitevők számát, amelyekre a Fermat-sejtés nem igaz. Ekkor
kitevők számát, amelyekre a Fermat-sejtés nem igaz. Ekkor ![]() mellett az
mellett az ![]() hányados 0-hoz tart.
hányados 0-hoz tart.
A fenti gondolatmenet szépséghibája, hogy bár nagyon sok kitevőre igazolja a Fermat-sejtést Faltings mély tételének felhasználásával, ezek között egyetlen prímszám sincsen. Márpedig a Fermat-sejtést elegendő prímszám kitevőkre igazolni. Mint látni fogjuk, ezek más módszerekkel érhetők el.
2. Elliptikus görbék és a Szpiro-sejtés
Az 1980-as években két olyan megközelítés is napvilágot látott, amely a Fermat-sejtést elliptikus görbék vizsgálatán keresztül kísérelte meg belátni. A kiinduló gondolat a következő. Legyen ![]() prímszám, és tegyük fel, hogy az
prímszám, és tegyük fel, hogy az ![]() relatív prím egészek teljesítik az
relatív prím egészek teljesítik az
egyenlőséget. Ekkor az
egyenlet által definiált projektív síkgörbének olyan tulajdonságai vannak, amelyek „túl szépek ahhoz, hogy ilyen görbe létezzen”. Ez a görbe az elliptikus görbék osztályába tartozik, és először Yves Hellegouarch, illetve Gerhard Frey vizsgálták a Fermat-sejtéssel kapcsolatban. Hogy miért túl szép ahhoz, hogy igaz legyen, annak magyarázatához szükségünk van néhány alapfogalomra elliptikus görbékkel kapcsolatban.
Általában a racionális számtest felett egy ![]() elliptikus görbét olyan
elliptikus görbét olyan
homogén harmadfokú egyenlet definiál, ahol az ![]() -k egymástól különböző komplex számok, és az egyenlőség jobboldalán álló tényezők szorzata racionális együtthatós polinom. Könnyen ellenőrizhető, hogy a fenti típusú egyenlet akkor és csak akkor definiál sima síkgörbét az előző szakasz értelmében, ha az
-k egymástól különböző komplex számok, és az egyenlőség jobboldalán álló tényezők szorzata racionális együtthatós polinom. Könnyen ellenőrizhető, hogy a fenti típusú egyenlet akkor és csak akkor definiál sima síkgörbét az előző szakasz értelmében, ha az ![]() -k különbözők. (Valóban: Ha
-k különbözők. (Valóban: Ha ![]() és az
és az ![]() szerinti parciális derivált 0, akkor
szerinti parciális derivált 0, akkor ![]() ; ekkor viszont az
; ekkor viszont az ![]() szerinti parciális derivált pontosan akkor nem 0, ha az
szerinti parciális derivált pontosan akkor nem 0, ha az ![]() -k különbözők.) Az egyszerűség kedvéért tegyük fel a továbbiakban, hogy az
-k különbözők.) Az egyszerűség kedvéért tegyük fel a továbbiakban, hogy az ![]() -k még egész számok is; a tárgyalás kiterjeszthető az általános esetre. Ha tehát az
-k még egész számok is; a tárgyalás kiterjeszthető az általános esetre. Ha tehát az ![]() -k egészek, akkor az egyenletet tekinthetjük modulo
-k egészek, akkor az egyenletet tekinthetjük modulo ![]() bármely
bármely ![]() prímszámra, és így egy olyan síkgörbét kapunk, amely a
prímszámra, és így egy olyan síkgörbét kapunk, amely a ![]() elemű test felett definiált. Ez azonban nem feltétlenül sima, hiszen bár az
elemű test felett definiált. Ez azonban nem feltétlenül sima, hiszen bár az ![]() -kről feltettük, hogy különbözőek, a mod
-kről feltettük, hogy különbözőek, a mod ![]() maradékosztályaik már nem feltétlenül azok.
maradékosztályaik már nem feltétlenül azok.
Hogy a mod ![]() redukciók viselkedését alaposabban tanulmányozhassuk, érdemes bevezetni az
redukciók viselkedését alaposabban tanulmányozhassuk, érdemes bevezetni az ![]() görbe diszkriminánsát: ez a
görbe diszkriminánsát: ez a
helyettesítésekkel kapott egyenlet ugyanazt a síkgörbét definiálja, de a diszkrimináns egy ![]() -es szorzóval változik. Belátható azonban, hogy csak a fenti típusú (polinomiális) helyettesítések őrzik meg az egyenlet fenti alakját. Így értelmes azt mondanunk, hogy az egyenlet
-es szorzóval változik. Belátható azonban, hogy csak a fenti típusú (polinomiális) helyettesítések őrzik meg az egyenlet fenti alakját. Így értelmes azt mondanunk, hogy az egyenlet ![]() -ra nézve minimális, ha a fenti típusú helyettesítéseket megengedve
-ra nézve minimális, ha a fenti típusú helyettesítéseket megengedve ![]() kitevője
kitevője ![]() -ben a lehető legkisebb. (Technikai okokból ez a definíció a
-ben a lehető legkisebb. (Technikai okokból ez a definíció a ![]() esetben módosításra szorul; ezt most nem részletezzük.) Egy nehéz tétel szerint a racionális számtest felett minden elliptikus görbének létezik olyan egyenlete, amely minden prímszámra egyszerre minimális: ez a minimális egyenlet.
esetben módosításra szorul; ezt most nem részletezzük.) Egy nehéz tétel szerint a racionális számtest felett minden elliptikus görbének létezik olyan egyenlete, amely minden prímszámra egyszerre minimális: ez a minimális egyenlet.
Azt mondjuk, hogy az ![]() görbének
görbének ![]() -ban jó a redukciója, ha a minimális egyenlet mod
-ban jó a redukciója, ha a minimális egyenlet mod ![]() redukciója sima. A rossz redukciónál két eset van: a kevésbé rossz az, ha a mod
redukciója sima. A rossz redukciónál két eset van: a kevésbé rossz az, ha a mod ![]() redukciónál két
redukciónál két ![]() fut össze, a rosszabb az, ha mind a három. (Geometriailag ezek úgynevezett csomó (node), illetve csúcs (cusp) szingularitásoknak felelnek meg.) A diszkriminánsra pillantva látjuk, hogy adott elliptikus görbének véges sok kivétellel minden prímre jó a redukciója. John Tate egy tétele szerint minden görbéhez található legalább egy olyan prím, ahol rossz a redukció. Az viszont gyakran előfordul, hogy a rossz redukciójú prímek mind az imént említett „kevésbé rossz” kategóriába tartoznak, az ilyen elliptikus görbéket hívjuk szemistabilnak. Ellenőrizhető, hogy a Fermat-sejtéshez tartozó fenti Hellegouarch—Frey görbék szemistabilak.
fut össze, a rosszabb az, ha mind a három. (Geometriailag ezek úgynevezett csomó (node), illetve csúcs (cusp) szingularitásoknak felelnek meg.) A diszkriminánsra pillantva látjuk, hogy adott elliptikus görbének véges sok kivétellel minden prímre jó a redukciója. John Tate egy tétele szerint minden görbéhez található legalább egy olyan prím, ahol rossz a redukció. Az viszont gyakran előfordul, hogy a rossz redukciójú prímek mind az imént említett „kevésbé rossz” kategóriába tartoznak, az ilyen elliptikus görbéket hívjuk szemistabilnak. Ellenőrizhető, hogy a Fermat-sejtéshez tartozó fenti Hellegouarch—Frey görbék szemistabilak.

Most már kimondhatjuk Lucien Szpiro 1980-as évekből származó sejtését, amely lényegében azt állítja, hogy szemistabil görbe esetén a diszkriminánsban előforduló prímek kitevői nem lehetnek túl nagyok. A pontos állításhoz vezessük be az ![]() nemnulla egész szám radikáljának fogalmát:
nemnulla egész szám radikáljának fogalmát: ![]() az
az ![]() prímosztóinak szorzata. A Szpiro-sejtést két formában szokás megfogalmazni.
prímosztóinak szorzata. A Szpiro-sejtést két formában szokás megfogalmazni.
Gyenge Szpiro-sejtés. Legyen ![]() szemistabil elliptikus görbe a racionális számtest felett. Ekkor léteznek
szemistabil elliptikus görbe a racionális számtest felett. Ekkor léteznek ![]() konstansok, amelyekre a minimális egyenlet
konstansok, amelyekre a minimális egyenlet ![]() diszkriminánsa teljesíti a
diszkriminánsa teljesíti a
egyenlőséget. (Amikor az ![]() -k egészek, a baloldalon természetesen elhagyható az abszolút érték, de általában nem.)
-k egészek, a baloldalon természetesen elhagyható az abszolút érték, de általában nem.)
Erős Szpiro-sejtés. A fenti szituációban minden ![]() valós számra létezik olyan
valós számra létezik olyan ![]() konstans, amelyre
konstans, amelyre
Az utóbbi sejtésben azért szerepel a ![]() kitevő, mert a 6-os kitevőre létezik ellenpélda.
kitevő, mert a 6-os kitevőre létezik ellenpélda.
Alkalmazzuk a Szpiro-sejtést a fenti Hellegouarch—Frey görbére, amelynek emlékeztetőül az egyenlete ![]() , ahol
, ahol ![]() valamely
valamely ![]() relatív prím egészekkel. Ennek a görbének a diszkriminánsa
relatív prím egészekkel. Ennek a görbének a diszkriminánsa
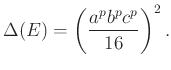
Látható, hogy elég nagy ![]() -re sérül a gyenge Szpiro-sejtés, az erős Szpiro-sejtés pedig már
-re sérül a gyenge Szpiro-sejtés, az erős Szpiro-sejtés pedig már ![]() -re nem teljesül. Más szóval nem létezik
-re nem teljesül. Más szóval nem létezik ![]() számhármas a fenti tulajdonságokkal, tehát az erős Szpiro-sejtésből következik a Fermat-sejtés
számhármas a fenti tulajdonságokkal, tehát az erős Szpiro-sejtésből következik a Fermat-sejtés ![]() esete.
esete.
Szpiro a fenti sejtésre az úgynevezett effektív Mordell-sejtés tanulmányozása során jutott. Ez utóbbi, mint már említettük, Faltings tételének azon élesítése, amely adott görbe racionális pontjainak koordinátáira kiszámítható korlátot is ad. Szpiro és Moret-Bailly megmutatták, hogy az effektív Mordell-sejtésből következik a gyenge Szpiro-sejtés (tehát a Fermat-sejtés is elég nagy ![]() kitevőre). Ráadásul a bizonyításból látszik, hogy elég az effektív Mordell-sejtést egyetlen görbére ismerni ehhez a konklúzióhoz, tehát az előző szakaszban vázolt gondolatmenettel ellentétben nem kell végtelen sok egyenletre alkalmazni az effektív Mordell-sejtést ahhoz, hogy a Fermat-sejtést belássuk.
kitevőre). Ráadásul a bizonyításból látszik, hogy elég az effektív Mordell-sejtést egyetlen görbére ismerni ehhez a konklúzióhoz, tehát az előző szakaszban vázolt gondolatmenettel ellentétben nem kell végtelen sok egyenletre alkalmazni az effektív Mordell-sejtést ahhoz, hogy a Fermat-sejtést belássuk.
Másrészről Elkies belátta, hogy a Szpiro-sejtés egy módosított változatából (amely ekvivalens a híres abc-sejtéssel) következik a Mordell-sejtés, vagyis Faltings tétele. Ha e változat effektíven kiszámítható konstansokkal is ismert lenne, akkor az effektív Mordell-sejtés is következne.
2012-ben Shinichi Mochizuki nyilvánosságra hozott négy igen hosszú kéziratot, amelyeknek eredményeiből állítása szerint következik a Szpiro-sejtés erős és módosított formája is. 2016-ban Vesselin Dimitrov megmutatta, hogy amennyiben Mochizuki eredményei helyesek, akkor a sejtések effektív verziója is igaz. Mochizuki rendkívül bonyolult bizonyításait jelen pillanatig még nem dolgozta fel a nemzetközi matematikusközösség.
3. Moduláris formák és a Serre-sejtések
A Fermat-sejtéshez vezető másik módszer a moduláris formák elméletének segítségével mutatja meg, hogy az Hellegouarch—Frey görbe nem létezhet. Ez az az út, amelyen Andrew Wiles sikeresen eljutott a Fermat-sejtés igazolásához. Azóta azonban a Wilesénál erősebb eredmények is ismertek, amelyekből könnyebb levezetni a Fermat-sejtést, így az alábbiakban ezeket ismertetjük röviden.
Először is meg kell ismerkednünk az elliptikus görbékhez tartozó Galois-reprezentációk fogalmával. Diofantoszig nyúlik vissza az úgynevezett húr-érintő módszer, amellyel egy racionális számtest feletti elliptikus görbe pontjain összeadás definiálható (erről az olvasó Tóth Árpád minapi cikkében talál többet). Erre az összeadásra nézve a pontok Abel-csoportot alkotnak. Bennünket kizárólag a véges rendű elemek fognak érdekelni ebben az Abel-csoportban.
Tekintsük egy pillanatra a görbét a komplex számtest felett. Ekkor minden ![]() -re belátható, hogy az
-re belátható, hogy az ![]() -t osztó rendű komplex pontok részcsoportja izomorf a
-t osztó rendű komplex pontok részcsoportja izomorf a ![]() csoporttal. (A Riemann-felületek elméletében jártas olvasó tudja is, hogy miért: az elliptikus görbe komplex pontjainak sokasága holomorf módon izomorf egy komplex tórusszal, és ennél az izomorfizmusnál az összeadás pont abba az összeadásba megy át a tóruszon, amelyet úgy kapunk, hogy tekintjük a komplex síkot a szokásos összeadással, és lefaktorizálunk egy alkalmas parallelogrammaráccsal. Az
csoporttal. (A Riemann-felületek elméletében jártas olvasó tudja is, hogy miért: az elliptikus görbe komplex pontjainak sokasága holomorf módon izomorf egy komplex tórusszal, és ennél az izomorfizmusnál az összeadás pont abba az összeadásba megy át a tóruszon, amelyet úgy kapunk, hogy tekintjük a komplex síkot a szokásos összeadással, és lefaktorizálunk egy alkalmas parallelogrammaráccsal. Az ![]() rendű pontok így a rács „
rendű pontok így a rács „![]() -szeres besűrítéséből” adódnak.)
-szeres besűrítéséből” adódnak.)
Ha most az ![]() elliptikus görbe
elliptikus görbe ![]() felett definiált, akkor belátható, hogy létezik olyan
felett definiált, akkor belátható, hogy létezik olyan ![]() véges testbővítés, amelyre az
véges testbővítés, amelyre az ![]() -t osztó rendű pontok koordinátái mind
-t osztó rendű pontok koordinátái mind ![]() -ban vannak. Feltehető, hogy
-ban vannak. Feltehető, hogy ![]() Galois-bővítés. Ekkor a
Galois-bővítés. Ekkor a ![]() Galois-csoport hat az
Galois-csoport hat az ![]() -t osztó rendű pontok koordinátáin, és ezáltal a
-t osztó rendű pontok koordinátáin, és ezáltal a ![]() csoporton. Ha itt
csoporton. Ha itt ![]() prímszám, akkor tehát az
prímszám, akkor tehát az ![]() véges test feletti 2-dimenziós vektortéren kapunk egy csoportreprezentációt. A kapott
véges test feletti 2-dimenziós vektortéren kapunk egy csoportreprezentációt. A kapott
reprezentációt az ![]() -hez tartozó Galois-reprezentációnak nevezzük. (Belátható, hogy ez — megfelelő értelemben véve — nem függ
-hez tartozó Galois-reprezentációnak nevezzük. (Belátható, hogy ez — megfelelő értelemben véve — nem függ ![]() -tól.)
-tól.)
Most egy időre elhagyjuk az elliptikus görbéket, és egy másik módon, moduláris formák segítségével definiálunk Galois-reprezentációkat. Kezdjük a moduláris formák elméletének nagyon rövid alapvetésével; egy általánosabb kontextusban továbbiak olvashatók a témában Harcos Gergely cikkében.
Adott ![]() egész szám mellett tekintsük a
egész szám mellett tekintsük a
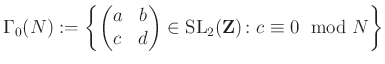
csoportot, amely tört-lineáris transzformációk által hat a
komplex felső félsíkon:
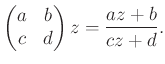
Adott ![]() páros pozitív egész szám mellett egy
páros pozitív egész szám mellett egy ![]() holomorf függvényt
holomorf függvényt ![]() súlyú,
súlyú, ![]() szintű moduláris formának mondunk, ha teljesíti az
szintű moduláris formának mondunk, ha teljesíti az
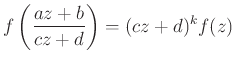
azonosságot minden ![]() -beli mátrix hatására nézve. Mivel speciálisan a
-beli mátrix hatására nézve. Mivel speciálisan a ![]() eltolások is előállnak egy
eltolások is előállnak egy ![]() -beli mátrix hatásaként (ahol
-beli mátrix hatásaként (ahol ![]() ,
, ![]() ), a függvény erre az eltolásra nézve periodikus, így sorba fejthető a
), a függvény erre az eltolásra nézve periodikus, így sorba fejthető a ![]() paraméter szerint. Azt mondjuk, hogy
paraméter szerint. Azt mondjuk, hogy ![]() csúcsforma, ha e sorfejtés holomorfan kiterjed
csúcsforma, ha e sorfejtés holomorfan kiterjed ![]() -ba is, és ott 0 értéket vesz fel. Ilyenkor tehát kapunk egy
-ba is, és ott 0 értéket vesz fel. Ilyenkor tehát kapunk egy
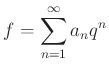
előállítást.
Adott ![]() pár mellett a
pár mellett a ![]() súlyú és
súlyú és ![]() szintű moduláris formák lineáris alteret alkotnak a
szintű moduláris formák lineáris alteret alkotnak a ![]() függvények
függvények ![]() -vektorterében, amelyről megmutatható, hogy véges dimenziós. E véges dimenziós vektortéren definiáljuk most lineáris operátorok egy családját. Adott
-vektorterében, amelyről megmutatható, hogy véges dimenziós. E véges dimenziós vektortéren definiáljuk most lineáris operátorok egy családját. Adott ![]() prímszám mellett a
prímszám mellett a ![]() Hecke-operátort a
Hecke-operátort a
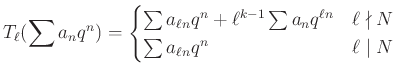
formulák definiálják. Megmutatható, hogy a ![]() operátorok páronként kommutálnak egymással, így egy ismert lineáris algebrai tétel szerint közös bázisban diagonalizálhatók. Az is igaz továbbá, hogy ha az
operátorok páronként kommutálnak egymással, így egy ismert lineáris algebrai tétel szerint közös bázisban diagonalizálhatók. Az is igaz továbbá, hogy ha az ![]() moduláris forma közös sajátvektora a
moduláris forma közös sajátvektora a ![]() operátoroknak, amelyet úgy normalizálunk, hogy
operátoroknak, amelyet úgy normalizálunk, hogy ![]() teljesül, akkor az
teljesül, akkor az ![]() együttható épp a
együttható épp a ![]() operátorhoz tartozó sajátérték lesz.
operátorhoz tartozó sajátérték lesz.

Most már eljutottunk Pierre Deligne egy konstrukciójához, amely fenti tulajdonságú moduláris formáknak Galois-reprezentációkat feleltet meg oly módon, hogy a reprezentációt a Galois-csoport bizonyos kitüntetett elemeinek képei karakterizálják. A kitüntetett elemek a következők: minden ![]() prímszámhoz tartozik a
prímszámhoz tartozik a ![]() véges Galois-csoportban egy
véges Galois-csoportban egy ![]() „Frobenius-elem”. Ezeket véges sok
„Frobenius-elem”. Ezeket véges sok ![]() kivételével az a tulajdonság karakterizálja — konjugáltság erejéig —, hogy minden
kivételével az a tulajdonság karakterizálja — konjugáltság erejéig —, hogy minden ![]() algebrai egészre teljesül a
algebrai egészre teljesül a ![]() mod
mod ![]() kongruencia. (A hiányzó
kongruencia. (A hiányzó ![]() -ekre a definíció bonyolultabb.)
-ekre a definíció bonyolultabb.)
Deligne tétele. Legyen ![]() olyan csúcsforma, amely közös sajátvektora a
olyan csúcsforma, amely közös sajátvektora a ![]() Hecke-operátoroknak,
Hecke-operátoroknak, ![]() pedig prímszám (amely nem tévesztendő össze a
pedig prímszám (amely nem tévesztendő össze a ![]() paraméterrel). Ekkor létezik
paraméterrel). Ekkor létezik ![]() véges Galois-bővítés és
véges Galois-bővítés és
reprezentáció, amely véges sok kivétellel minden ![]() prímszámra teljesíti a
prímszámra teljesíti a
egyenlőségeket, ahol ![]() a
a ![]() -hez tartozó sajátérték. A fenti tulajdonságú
-hez tartozó sajátérték. A fenti tulajdonságú ![]() izomorfia erejéig egyértelműen meghatározott. (Itt a szokásos módon Tr egy mátrix nyomát, det pedig a determinánsát jelöli.)
izomorfia erejéig egyértelműen meghatározott. (Itt a szokásos módon Tr egy mátrix nyomát, det pedig a determinánsát jelöli.)

Numerikus evidencia alapján Jean-Pierre Serre az 1980-as években azt sejtette, hogy szinte minden irreducibilis ![]() reprezentáció megkapható a fenti módon. Serre sejtését korábbi részeredmények után 2009-ben teljes egészében igazolta Chandrashekhar Khare és Jean-Pierre Winterberger:
reprezentáció megkapható a fenti módon. Serre sejtését korábbi részeredmények után 2009-ben teljes egészében igazolta Chandrashekhar Khare és Jean-Pierre Winterberger:
Khare—Winterberger-tétel. Legyen ![]() irreducibilis reprezentáció, amelyre
irreducibilis reprezentáció, amelyre ![]() , ahol
, ahol ![]() az
az ![]() komplex konjugálást jelöli. Ekkor létezik olyan
komplex konjugálást jelöli. Ekkor létezik olyan ![]() moduláris forma, amelyre a Deligne-féle konstrukcióval kapott reprezentáció éppen
moduláris forma, amelyre a Deligne-féle konstrukcióval kapott reprezentáció éppen ![]() lesz. Ezen felül az
lesz. Ezen felül az ![]() súlya és szintje is tisztán algebrai módon meghatározható a
súlya és szintje is tisztán algebrai módon meghatározható a ![]() reprezentáció bizonyos invariánsainak segítségével.
reprezentáció bizonyos invariánsainak segítségével.
S hogy mi köze van mindennek a Fermat-sejtéshez? Térjünk csak vissza az ![]() Hellegouarch—Frey-féle elliptikus görbéhez. Korábban láttuk, hogy ehhez a görbéhez tartozik egy
Hellegouarch—Frey-féle elliptikus görbéhez. Korábban láttuk, hogy ehhez a görbéhez tartozik egy ![]() reprezentáció. Mint Serre rámutatott, Barry Mazur egy mély tételéből könnyen adódik, hogy e reprezentáció irreducibilis. Ellenőrizhető továbbá, hogy a
reprezentáció. Mint Serre rámutatott, Barry Mazur egy mély tételéből könnyen adódik, hogy e reprezentáció irreducibilis. Ellenőrizhető továbbá, hogy a ![]() feltétel is teljesül, és így a fenti tétel alkalmazható. Kapunk tehát egy moduláris formát, amelynek ráadásul ismerjük a
feltétel is teljesül, és így a fenti tétel alkalmazható. Kapunk tehát egy moduláris formát, amelynek ráadásul ismerjük a ![]() súlyát és az
súlyát és az ![]() szintjét is. A konkrét esetben kiszámítható, hogy
szintjét is. A konkrét esetben kiszámítható, hogy ![]() . Azonban régóta ismert, hogy ilyen moduláris forma nincs! Ez az ellentmondás adja, hogy az Hellegouarch—Frey-görbe nem létezik, tehát a
. Azonban régóta ismert, hogy ilyen moduláris forma nincs! Ez az ellentmondás adja, hogy az Hellegouarch—Frey-görbe nem létezik, tehát a ![]() kitevőjű Fermat-egyenletnek sincs nemtriviális megoldása.
kitevőjű Fermat-egyenletnek sincs nemtriviális megoldása.

Amikor Andrew Wiles az 1980-as évek végén elkezdett a Fermat-sejtésen dolgozni, Serre sejtésének csak egyetlen nemtriviális esete volt ismert, az úgynevezett Langlands—Tunnell-tétel. Ez az igen nehéz eredmény bizonyos speciális Galois-reprezentációkhoz konstruált moduláris formát a ![]() esetben. Ebből kiindulva Wiles belátta, hogy ha egy szemistabil elliptikus görbéhez tartozó azon
esetben. Ebből kiindulva Wiles belátta, hogy ha egy szemistabil elliptikus görbéhez tartozó azon ![]() Galois-reprezentációt tekintjük, amely nem az
Galois-reprezentációt tekintjük, amely nem az ![]() -beli együtthatós mátrixok gyűrűjébe képez, hanem a
-beli együtthatós mátrixok gyűrűjébe képez, hanem a ![]() -adikus számok teste feletti
-adikus számok teste feletti ![]() -es mátrixokéba (ehhez az elliptikus görbe
-es mátrixokéba (ehhez az elliptikus görbe ![]() rendű pontjait kell tekinteni minden
rendű pontjait kell tekinteni minden ![]() -re), akkor létezik olyan moduláris forma, amelyből
-re), akkor létezik olyan moduláris forma, amelyből ![]() megkapható egy a fentihez hasonló konstrukció segítségével. Ez az állítás Taniyama—Weil-sejtés (vagy modularitási sejtés) néven volt ismert, és tetszőleges elliptikus görbékre később Breuil, Conrad, Diamond és Taylor igazolták Wiles módszerének továbbfejlesztésével. Ebből az állításból azonban a Fermat-sejtés nem vezethető le olyan röviden, mint a Khare—Winterberger-tételből, szükség volt még Ken Ribet egy nehéz technikai eredményére is. Természetesen Khare és Wintenberger bizonyítása használja mindazon technikákat, amelyeket Ribet, Wiles és Taylor korábban kifejlesztettek.
megkapható egy a fentihez hasonló konstrukció segítségével. Ez az állítás Taniyama—Weil-sejtés (vagy modularitási sejtés) néven volt ismert, és tetszőleges elliptikus görbékre később Breuil, Conrad, Diamond és Taylor igazolták Wiles módszerének továbbfejlesztésével. Ebből az állításból azonban a Fermat-sejtés nem vezethető le olyan röviden, mint a Khare—Winterberger-tételből, szükség volt még Ken Ribet egy nehéz technikai eredményére is. Természetesen Khare és Wintenberger bizonyítása használja mindazon technikákat, amelyeket Ribet, Wiles és Taylor korábban kifejlesztettek.
A Galois-reprezentációk és a moduláris (vagy általánosabban automorf) formák kapcsolatának vizsgálata ma is az algebrai számelmélet egyik legaktívabb területe, amelynek számos mély alkalmazása van. Hogy zárásképpen visszakanyarodjunk fejtegetéseink elejéhez, említsük meg példaként Minhyong Kim egy nagy hatású eredményét, amely szerint ha tudnánk bizonyos magasabb dimenziós Galois-reprezentációkról, hogy automorf formákból jönnek, akkor új, az eddigiektől teljesen különböző bizonyítást kapnánk Faltings tételére!
Hálásan köszönöm Zábrádi Gergely sasszemű észrevételeit.
Szamuely Tamás
MTA Rényi Alfréd Matematikai Kutatóintézet
Bevezető irodalom a cikkben tárgyalt témákhoz:
- F. Diamond, J. Shurman. A First Course in Modular Forms, Springer, 2005.
- Y. Hellegouarch, Invitation to the Mathematics of Fermat—Wiles, Academic Press, 2001.
- J. H. Silverman, The Arithmetic of Elliptic Curves, Springer, 1986.
Az idézett tételek forrásai:
- C. Breuil, B. Conrad, F. Diamond, and R. Taylor, On the modularity of ellipic curves over
 : wild 3-adic exercises, J. Amer. Math. Soc. 14 (2001), 843—939.
: wild 3-adic exercises, J. Amer. Math. Soc. 14 (2001), 843—939. - P. Deligne, Formes modulaires et représentations
 -adiques, Séminaire Bourbaki, vol. 11 (1968—1969), 139—172.
-adiques, Séminaire Bourbaki, vol. 11 (1968—1969), 139—172. - V. Dimitrov, Effectivity in Mochizuki's work on the abc-conjecture, preprint arXiv:1601.03572.
- N. Elkies, ABC implies Mordell, Intern. Math. Research Notices 7 (1991), 99—109.
- G. Faltings, Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. math. 73 (1983), 349—366.
- A Granville, The set of exponents for which Fermat's Last Theorem is true has density one, C. R. Acad. Sci. Canada 7 (1985), 55—60.
- R. Heath-Brown, Fermat's Last Theorem for “Almost All” Exponents, Bull. London Math. Soc. 17 (1985), 15—16.
- C. Khare, J-P. Wintenberger, Serre’s modularity conjecture (I), Invent. math. 178 (2009), 485—504.
- M. Kim, The unipotent Albanese map and Selmer varieties for curves, Publ. Res. Inst. Math. Sci. 45 (2009), 89—133.
- S. Mochizuki, Inter-universal Teichmüller Theory I-IV, preprints, 2012.
- J. Oesterlé, Nouvelles approches du «théorème» de Fermat, Séminaire Bourbaki, vol. 30 (1987—1988), 165—186.
- K. Ribet, On modular representations of
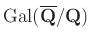 arising from modular forms, Invent. math. 100 (1990), 431—476.
arising from modular forms, Invent. math. 100 (1990), 431—476. - J-P. Serre, Sur les représentations modulaires de degré 2 de
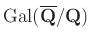 , Duke Math. J. 54 (1987), 179—230
, Duke Math. J. 54 (1987), 179—230 - L. Szpiro et al., Séminaire sur les pinceaux de courbes elliptiques, Astérisque 183, 1990.
- A. Wiles, Modular elliptic curves and Fermat's last theorem, Ann. of Math. 141 (1995), 443—551.
A fényképek forrásai:
- Gerd Faltings, német matematikus, szül. 1954. (Max Planck Matematikai Intézet, Bonni Egyetem, Princeton Egyetem, Wuppertal Egyetem) https://en.wikipedia.org/wiki/Gerd_Faltings (Copyright MSO, Renate Schmid http://owpdb.mfo.de/detail?photoID=7513 )
- Lucien Szpiro, francia matematikus, szül. 1941. (City University of New York) https://en.wikipedia.org/wiki/Lucien_Szpiro (Copyright MSO, Renate Schmid http://owpdb.mfo.de/detail?photo_id=7514 )
- Pierre Deligne, belga matematikus, szül. 1944. (Institute for Advanced Study Princeton, Institut des Hautes Études Scientifiques) https://www.ias.edu/scholars/deligne
- Jean-Pierre Serre, francia matematikus, szül. 1926. (Centre National de la Recherche Scientifique) https://en.wikipedia.org/wiki/Jean-Pierre_Serre
- Andrew Wiles, angol matematikus, szül. 1953. (University of Oxford, Princeton University)
https://en.wikipedia.org/wiki/Andrew_Wiles : Andrew Wiles 1995 októberében Beaumont-d-Lomagne-ban, Fermat emlékműve előtt - Klaus Barner képe.









