A 2017. évi Abel-díjat Yves Meyer francia matematikus kapta a waveletek matematikai elméletének kidolgozásában játszott úttörő munkásságáért. Szeizmikus adatok elemzésére és képek tömörítésére használt gyakorlati eljárásokból kiindulva az 1980-as évek közepétől vezetésével a jelfeldolgozás egy új, hatékony módszerének rakták le a matematikai alapjait. A Fourier-analízisben korábban alkalmazott trigonometrikus felbontás helyett rövid tartójú hullám, ún. wavelet (franciául: ondelette) összetevőket használtak. A szakirodalomban a legtöbb nyelven átvették az angol elnevezést, hazánkban is ez terjedt el. (Egyik tanítványom a hullámka elnevezés használatát javasolta.) Meyer nevéhez fűződik az első sima, ortonormált wavelet-bázis konstrukciója, valamint a jelek felbontására használt multirezolúciós analízis (MR) bevezetése. A waveletek elmélete rövid időn belül igen népszerű lett az adatátvitellel és a jel- és képfeldolgozással foglalkozó szakemberek körében. Az elmúlt három évtizedben a wavelet-analízis számos változatát alkalmazták, többek között a harmonikus analízis, a jeltömörítés, a hibaredukció és a képfeldolgozás problémáinak megoldására. Az eljárást felhasználták a Hubble űrteleszkóp felvételeinek dekonvolúciójára, valamint a napjainkban észlelt gravitációs hullámok detektálásában. Yves Meyernek ezen túlmenően alapvető eredményei vannak a számelmélet, a harmonikus analízis, a parciális differenciálegyenletek, speciálisan a Navier-Stokes-egyenletek, valamint a szinguláris integrálegyenletek elméletében.

Ebben a dolgozatban ismertetjük a témakör előzményeit, vázoljuk matematikai hátterét. Külön figyelmet szentelünk a magyar matematikusok eredményeire, amelyek jelentősége az irányításelmélet, a jelfeldolgázás és a waveletek területén új megvilágításba kerültek. Például a trigonometrikus Fourier-sorokra vonatkozó Fejér-féle szummáció a háromszög ablaknak megfelelő jelszűrési eljárásként interpretálható. Számos, Riesz Frigyes által bevezetett fogalom és nevéhez fűződő eredmény alapvető szerepet játszik ezekben az alkalmazásokban. Ezek közül a matematikusok körében jól ismert klasszikus tételein túlmenően itt most csak a Hardy-terek faktorizációjára, a róla elnevezett bázis fogalmára, valamint a nemnegatív trigonometrikus polinomok előállítására vonatkozó Fejér-Riesz-féle tételre utalunk, amelyek a wavelet konstrukciók alapvető eszközeivé váltak.

A Haar Alfrédről elnevezett mérték, amely az absztrakt harmonikus analízis egyik legfontosabb eszköze, a jelfeldolgozás transzformációinak leírásában is nélkülözhetetlennek bizonyult. A róla elnevezett rendszer, amelyet 1909-ben egy elméleti probléma tisztázására vezetett be, napjainkban mint a legegyszerűbb wavelet vált igazán ismertté. Míg az 1960-as években, egyfajta magyar specialitásként, kizárólag csak a hazai egyetemi tankönyvek tesznek említést a Haar-rendszerről [13], addig manapság szinte minden jelfeldolgozással kapcsolatos tankönyv több fejezetet szentel a témának.

A Haar-rendszerből kiinduló wavelet-transzformáció mellett a Gábor Dénes által 1945-ben vizsgált (ablakos) Fourier-transzformáció (azóta Gábor-transzformációnak nevezett eljárás) a beszéd és zenei hangok elemzésének hatékony eszköze lett. Ez a transzformáció a waveletek egy másik típusának mintájául szolgál. Az utóbbi két évtizedben a wavelet-transzformációk számos további változatát vezették be és alkalmazták a matematika, a természet- és műszaki tudományok különböző területein. Ezek a transzformációk, a klasszikus Fourier-transzformációhoz hasonlóan, egységes elvek szerint származtathatók, felhasználva az absztrakt harmonikus analízis eszköztárát. Ezen az úton, kiindulva az affin csoport egy reprezentációjából eljuthatunk az (affin) wavelet-transzformációhoz, a Heisenberg-féle csoport egy reprezentációjából a Gábor-transzformációhoz. A waveletek 2000 óta az ELTE alkalmazott matematikus és informatikus szakán speciális szakirányok tanterveinek, PhD programok és kutatások részét képezik [11], [16]. Kiindulva a Bolyai-Lobacsevszkij-féle geometria egybevágósági transzformációiból, a fentiek mintájára bevezettük a hiperbolikus wavelet transzformációkat (HWT-t) [12]. A szóban forgó egybevágósági transzformációk a Blaschke-függvényekkel írhatók le. Ezek nemcsak a komplex függvénytanban, hanem az irányításelméletben is kitüntetett szerepet játszanak. Ennek alapján azt reméljük, hogy a HWT a jelfeldolgozásnak és a rendszerelméleti alkalmazásoknak adekvát eszközévé válhat. Az MTA SZTAKI és az ELTE Numerikus Analízis Tanszék együttműködésében született eredmények azt mutatják, hogy ezek a transzformációk hatékonyan alkalmazhatók az irányításelméletben [1] és EKG jelek feldolgozásására és tömörítésére [4].
Történeti áttekintés
A Fourier-sorok elméletének kialakulása szorosan összefügg fontos gyakorlati problémákkal. Már maga Fourier is egy fizikából származó feladat, a hővezetés matematikai leírására dolgozta ki módszerét. A matematika számos fejezetének létrejötte és fejlődése szorosan összefügg azokkal a kérdésekkel, amelyek a Fourier-sorok alkalmazásával kapcsolatban felvetődtek. Ezek tisztázása, Dirichlet munkássága nyomán a ma is használt függvényfogalom kialakulásához vezettek, Cantort a Fourier-sorok konvergencia halmazaival kapcsolatos vizsgálatai inspirálták a halmazelmélet megalapozására. Riemann a Fourier-együtthatók értelmezéséhez kiterjesztette az integrál fogalmát, Lebesgue a róla elnevezett integrál bevezetésével a Fourier-sorok elméletét gazdagította egy ma is nélkülözhetetlen eszközzel, amely azután a valószínűségelmélet matematikai megalapozásában is fontos szerepet játszott.
Az első, mai szemmel nézve is korrekt konvergenciatétel Dirichlet-től származik, aki 1829-ben bebizonyította, hogy a szakaszonként monoton függvények Fourier-sora konvergens. Már 1876-ban Du Bois Reymond munkássága révén ismert volt, hogy a Fourier-sor ![]() -szerint periodikus, folytonos függvény esetén is lehet divergens. A Fourier-sorok konvergenciájával kapcsolatos problémák tisztázása kapcsán új fogalmakat és módszereket vezettek be, több új fejezettel gazdagítva a matematikát. Többek között a hagyományos, pontonkénti konvergencia helyett az integrálközépben való konvergenciát, a részletösszegek helyett azok számtani közepeinek konvergenciáját véve alapul számos problémára sikerült választ adni. Ezekben Riesz Frigyes és Fejér Lipót munkássága úttörő jellegű volt [13].
-szerint periodikus, folytonos függvény esetén is lehet divergens. A Fourier-sorok konvergenciájával kapcsolatos problémák tisztázása kapcsán új fogalmakat és módszereket vezettek be, több új fejezettel gazdagítva a matematikát. Többek között a hagyományos, pontonkénti konvergencia helyett az integrálközépben való konvergenciát, a részletösszegek helyett azok számtani közepeinek konvergenciáját véve alapul számos problémára sikerült választ adni. Ezekben Riesz Frigyes és Fejér Lipót munkássága úttörő jellegű volt [13].
A Haar-rendszer
Már a múlt század elején a trigonometrikus rendszer mellett több, akkor kissé egzotikusnak tűnő függvényrendszert vezettek be, amelyek elméleti és gyakorlati jelentősége jóval később derült ki. Ezek között is a Haar Alfréd által definiált ortonormált rendszer játszik kitüntetett szerepet. Haar a róla elnevezett rendszert doktori értekezésében vezette be 1909-ben, választ adva Hilbert egy Fourier-sorok divergenciájával kapcsolatos problémájára. A Du Bois Reymond-féle ellenpéldával összefüggésben Hilbert felvetette, hogy létezik-e olyan ortonormált rendszer, amely szerint vett Fourier-sorfejtés minden folytonos függvényre mindenütt konvergens? A kérdésre Haar pozitív választ adott, bebizonyítva, hogy az azóta róla elnevezett ( ![]() ) ortonormált rendszer szerinti Fourier-sor minden folytonos függvény esetén egyenletesen konvergens. Az első pillanatra mesterkéltnek tűnő rendszer lépcsős függvényekből áll, amely a
) ortonormált rendszer szerinti Fourier-sor minden folytonos függvény esetén egyenletesen konvergens. Az első pillanatra mesterkéltnek tűnő rendszer lépcsős függvényekből áll, amely a ![]() intervallumon értelmezett
intervallumon értelmezett ![]() alapfüggvényből egyszerűen származtatható, ahol
alapfüggvényből egyszerűen származtatható, ahol ![]() (
( ![]() ),
), ![]() (
( ![]() ),
), ![]() (
( ![]() ). Nevezetesen transzlációt és dilatációt alkalmazva kapjuk az
). Nevezetesen transzlációt és dilatációt alkalmazva kapjuk az ![]() intervallumon értelemzett
intervallumon értelemzett ![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() ) Haar-rendszert. A
) Haar-rendszert. A ![]() függvény tartója a
függvény tartója a ![]() hosszúságú
hosszúságú ![]() diadikus intervallum. Ebből következik, hogy az
diadikus intervallum. Ebből következik, hogy az ![]() függvény
függvény ![]() Haar-Fourier-együtthatói, ellentétben a trigonometrikus Fourier-együtthatókkal, az
Haar-Fourier-együtthatói, ellentétben a trigonometrikus Fourier-együtthatókkal, az ![]() függvénynek csak az
függvénynek csak az ![]() intervallumon felvett értékeitől függnek. A Haar-rendszer ortonormált az
intervallumon felvett értékeitől függnek. A Haar-rendszer ortonormált az ![]() Hilbert-tér szokásos skaláris szorzatára nézve és az
Hilbert-tér szokásos skaláris szorzatára nézve és az ![]() függvény Haar-Fourier-sorának
függvény Haar-Fourier-sorának ![]() részletösszegei előállíthatók az
részletösszegei előállíthatók az ![]() függvény diadikus intervallumokra vett integrálközepeivel, nevezetesen az
függvény diadikus intervallumokra vett integrálközepeivel, nevezetesen az ![]() pontokban
pontokban ![]() . Innen következik, hogy a Haar-rendszer teljes az
. Innen következik, hogy a Haar-rendszer teljes az ![]() térben, bármely
térben, bármely ![]() függvény Haar-Fourier-sora
függvény Haar-Fourier-sora ![]() -normában és m.m. konvergál az
-normában és m.m. konvergál az ![]() -hez, továbbá, választ adva Hilbert kérdésére, folytonos függvény esetén a konvergencia egyenletes. A Haar-rendszer ezekben a tulajdonságaiban alapvetően különbözik a trigonometrikus rendszertől.
-hez, továbbá, választ adva Hilbert kérdésére, folytonos függvény esetén a konvergencia egyenletes. A Haar-rendszer ezekben a tulajdonságaiban alapvetően különbözik a trigonometrikus rendszertől.
Valószínűségelméleti terminológiát használva ![]() a
a ![]() hosszúságú diadikus intervallumok által generált
hosszúságú diadikus intervallumok által generált ![]() -algebrára vonatkozó feltételes várható érték, továbbá az (
-algebrára vonatkozó feltételes várható érték, továbbá az (![]() ,
, ![]() ) részletösszegek (reguláris, diadikus) martingált alkotnak.
) részletösszegek (reguláris, diadikus) martingált alkotnak.
A Haar-rendszernek ezek a tulajdonságai szolgáltak a bázisokkal összefüggő funkcionálanalízisbeli, a martingálelméleti és a waveletekkel kapcsolatos vizsgálatok kiinduló pontjául.
Egyszerűen igazolható, hogy a Haar-rendszer nemcsak az ![]() Hilbert-térben, hanem az
Hilbert-térben, hanem az ![]() (
( ![]() ) Banach-terekben is bázist alkot. A Haar-sorok feltétlen (bármely átrendezés melletti) konvergenciájának vizsgálatában fontos szerepet játszik az
) Banach-terekben is bázist alkot. A Haar-sorok feltétlen (bármely átrendezés melletti) konvergenciájának vizsgálatában fontos szerepet játszik az ![]() függvény Paley által bevezetett
függvény Paley által bevezetett ![]() kvadratikus variációja. Paley bebizonyította, hogy
kvadratikus variációja. Paley bebizonyította, hogy ![]() esetén az
esetén az ![]() és a
és a ![]()
![]() -normái ekvivalensek. Ennek alapján Marcinkiewicz megmutatta, hogy a Haar-rendszer
-normái ekvivalensek. Ennek alapján Marcinkiewicz megmutatta, hogy a Haar-rendszer ![]() esetén feltétlen (azaz bármely átrendezés mellett is) bázis az
esetén feltétlen (azaz bármely átrendezés mellett is) bázis az ![]() térben. Ismeretes, hogy a Parseval-formula alapján az
térben. Ismeretes, hogy a Parseval-formula alapján az ![]() -tér jellemezhető bármely
-tér jellemezhető bármely ![]() teljes ortonormált rendszer szerint vett Fourier-együtthatókkal:
teljes ortonormált rendszer szerint vett Fourier-együtthatókkal: ![]() akkor és csak akkor, ha
akkor és csak akkor, ha ![]() . Amíg
. Amíg ![]() terekre
terekre ![]() esetén ilyen típusú jellemzés általában nem adható, addig a Haar-együtthatókból a
esetén ilyen típusú jellemzés általában nem adható, addig a Haar-együtthatókból a ![]() -ből kiindulva szerkeszthetünk az
-ből kiindulva szerkeszthetünk az ![]() -normával ekvivalens normát. A Haar-rendszernek ezek a tulajdonságai az 1960-as években, hosszú szünet után, ismét ráirányították a figyelmet a rendszerre. Orosz matematikusok munkássága révén kiderült, hogy a Haar-rendszer eredményesen alkalmazható a funkcionálanalízis fontos problémáinak megoldásában és kitüntetett szerepet játszik a bázisok között. Például többek között kiderült, hogy Banach-terek egy tág osztályára igaz a következő állítás: ha a szóban forgó Banach-térben a Haar-rendszer nem feltétlen bázis, akkor ebben a térben feltétlen bázis nem létezik. Speciálisan az
-normával ekvivalens normát. A Haar-rendszernek ezek a tulajdonságai az 1960-as években, hosszú szünet után, ismét ráirányították a figyelmet a rendszerre. Orosz matematikusok munkássága révén kiderült, hogy a Haar-rendszer eredményesen alkalmazható a funkcionálanalízis fontos problémáinak megoldásában és kitüntetett szerepet játszik a bázisok között. Például többek között kiderült, hogy Banach-terek egy tág osztályára igaz a következő állítás: ha a szóban forgó Banach-térben a Haar-rendszer nem feltétlen bázis, akkor ebben a térben feltétlen bázis nem létezik. Speciálisan az ![]() térben nincs feltétlen bázis. Ezekről az eredményekről nyújt részletes áttekintést Ciesielski [2] és Uljanov [14] 1985-ben a Haar emlékkonferencián tartott előadása és a [9] monográfia.
térben nincs feltétlen bázis. Ezekről az eredményekről nyújt részletes áttekintést Ciesielski [2] és Uljanov [14] 1985-ben a Haar emlékkonferencián tartott előadása és a [9] monográfia.
A Faber-Schauder-, a Franklin- és a Ciesielski-féle rendszer
Mivel a Haar-függvények nem folytonosak, azért ezek nem alkotnak bázist a ![]() függvénytérben. Faber 1910-ben a Haar-függvények integrálját véve bevezetett egy folytonos függvényekből álló rendszert, amely normáló faktortól eltekintve a
függvénytérben. Faber 1910-ben a Haar-függvények integrálját véve bevezetett egy folytonos függvényekből álló rendszert, amely normáló faktortól eltekintve a ![]() -hez hasonló alakban adható meg: Kiindulva a
-hez hasonló alakban adható meg: Kiindulva a ![]() ,,háztető'' függvényből a szóban forgó rendszer dilatációval és transzlációval származtatható:
,,háztető'' függvényből a szóban forgó rendszer dilatációval és transzlációval származtatható: ![]() (
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ). Faber megmutatta, hogy ez a rendszer bázis a
). Faber megmutatta, hogy ez a rendszer bázis a ![]() végpontjaiban eltűnő folytonos függvények
végpontjaiban eltűnő folytonos függvények ![]() terén. Ezekhez hozzávéve egy lineáris függvényt a
terén. Ezekhez hozzávéve egy lineáris függvényt a ![]() tér egy bázisát kapjuk. Megjegyezzük, hogy ezt a bázist később (1927-ben) Schauder újra felfedezte és azóta ezt a rendszert az irodalomban Faber-Schauder-féle (FS) rendszernek nevezzük. Ez a rendszer nyilván nem ortogonális az
tér egy bázisát kapjuk. Megjegyezzük, hogy ezt a bázist később (1927-ben) Schauder újra felfedezte és azóta ezt a rendszert az irodalomban Faber-Schauder-féle (FS) rendszernek nevezzük. Ez a rendszer nyilván nem ortogonális az ![]() -tér skaláris szorzatára nézve. A
-tér skaláris szorzatára nézve. A ![]() (
( ![]() ) reláció úgy interpretálható, hogy a folytonos függvényekből álló FS-rendszer és a korlátos változású függvényekből álló Haar-rendszer biortogonális. Megjegyezzük, hogy az
) reláció úgy interpretálható, hogy a folytonos függvényekből álló FS-rendszer és a korlátos változású függvényekből álló Haar-rendszer biortogonális. Megjegyezzük, hogy az ![]() függvény FS-rendszer szerinti biortogonális sorfejtésének részletösszegei interpolálnak a diadikusan racionális pontokban:
függvény FS-rendszer szerinti biortogonális sorfejtésének részletösszegei interpolálnak a diadikusan racionális pontokban: ![]() (
(![]() ,
, ![]() ,
, ![]() ), továbbá folytonos függvények FS-rendszer szerini biortogonális sorfejtése egyenletesen tart az
), továbbá folytonos függvények FS-rendszer szerini biortogonális sorfejtése egyenletesen tart az ![]() -hez.
-hez.
Franklin amerikai matematikus 1928-ban az FS-rendszerből kiindulva a Gram-Schmidt-féle ortogonalizációs eljárással bevezetett egy (szakaszonként lineáris, más szóval elsőfokú spline függvényekből álló) ortonormált rendszert, amelyről megmutatta, hogy nemcsak az ![]() térben, hanem
térben, hanem ![]() -ben is bázis. A Franklin-rendszer nem írható le a Haar-rendszerhez hasonló egyszerű képlettel. Ugyanakkor Ciesielski lengyel matematikus 1963-ban jól használható becslést adott a Franklin-rendszer függvényeire és Dirichlet-féle magfüggvényeire. Többek között bebizonyította, hogy az
-ben is bázis. A Franklin-rendszer nem írható le a Haar-rendszerhez hasonló egyszerű képlettel. Ugyanakkor Ciesielski lengyel matematikus 1963-ban jól használható becslést adott a Franklin-rendszer függvényeire és Dirichlet-féle magfüggvényeire. Többek között bebizonyította, hogy az ![]() (
(![]() ,
, ![]() ,
, ![]() ) Franklin-függvények a Haar-függvényhez hasonló függvényekkel becsülhetők:
) Franklin-függvények a Haar-függvényhez hasonló függvényekkel becsülhetők: ![]() , ahol
, ahol ![]() és
és ![]() abszolút pozitív konstansok. Ezeket az eredményeket általánosítva az FS rendszer helyett
abszolút pozitív konstansok. Ezeket az eredményeket általánosítva az FS rendszer helyett ![]() -edfokú spline függvényekből kiindulva Ciesielski az 1970-es években jó approximációs tulajdonságokkal rendelkező,
-edfokú spline függvényekből kiindulva Ciesielski az 1970-es években jó approximációs tulajdonságokkal rendelkező, ![]() -beli ortogonális bázisoknak egy új osztályát vezette be. Ezekkel több, Banach 1932-ben megjelent könyvében említett fontos térben sikerült bázist szerkeszteni. Felhasználva ezeket az eredményeket Bockarjev orosz matematikus bebizonyította a Paley-féle egyenlőtlenség megfelelőjét a Franklin-rendszerre, következésképpen kiderült, hogy
-beli ortogonális bázisoknak egy új osztályát vezette be. Ezekkel több, Banach 1932-ben megjelent könyvében említett fontos térben sikerült bázist szerkeszteni. Felhasználva ezeket az eredményeket Bockarjev orosz matematikus bebizonyította a Paley-féle egyenlőtlenség megfelelőjét a Franklin-rendszerre, következésképpen kiderült, hogy ![]() esetén a Franklin-rendszer is feltétlen bázist alkot az
esetén a Franklin-rendszer is feltétlen bázist alkot az ![]() -terekben. Ugyanitt a Franklin-rendszer analitikus kiterjesztésével bázist konstruált a diszkalgebrán, megoldva Banach egy hosszú ideig nyitott problémáját. Z. Ciesielski, Simon Péter és P. Sjölin megmutatták, hogy azonos együtthatókat véve a Haar- és Franklin-sorok
-terekben. Ugyanitt a Franklin-rendszer analitikus kiterjesztésével bázist konstruált a diszkalgebrán, megoldva Banach egy hosszú ideig nyitott problémáját. Z. Ciesielski, Simon Péter és P. Sjölin megmutatták, hogy azonos együtthatókat véve a Haar- és Franklin-sorok ![]() -normában ekvikonvergensek, ha
-normában ekvikonvergensek, ha ![]() más szóval a szóban forgó rendszerek ekvivalens bázisok az
más szóval a szóban forgó rendszerek ekvivalens bázisok az ![]() (
( ![]() ) terekben. Ez volt az első nem triviális példa ekvivalens bázisokra. Ezekről további információt nyújt a [9] könyv 5. fejezete.
) terekben. Ez volt az első nem triviális példa ekvivalens bázisokra. Ezekről további információt nyújt a [9] könyv 5. fejezete.
Waveletek
A jel- és képfeldolgozás gyakorlatában a jelek matematikai modellezése, analízise, kódolása, tömörítése, átvitele és tárolása, valamint szintézise és rekonstrukciója kapcsán számos új probléma vetődött fel, amelyek hagyományos eszközökkel nem kezelhetők. A klasszikus Fourier-transzformációt sikerrel alkalmazták stacionárius jelek reprezentálására. Az elmúlt évek tapasztalatai azt mutatják, hogy tranziens jelek esetén a wavelet-transzformációk bizonyultak hatékonyabbnak.
A Ciesielski-féle rendszereket és becsléseket felhasználva számos, bázisokkal kapcsolatos, fontos elméleti problémát sikerült megoldani. Az ezek szerinti sorfejtések, jó approximációs tulajdonságai miatt, alkalmasak sztohasztikus folyamatok leírására, jelek reprezentálására és hatékony tömörítésére. Ennek ellenére, talán explicit előállítás hiányában, ezek nem terjedtek el az alkalmazók körében.
Az 1980-as évektől egy másik irányba indultak el a kutatások a Haar-rendszerhez hasonlóan származtatható, sima függvényekből álló ![]() (
( ![]() ,
, ![]() ) alakú ortonormált rendszerek konstrukcióját tűzve ki célul az
) alakú ortonormált rendszerek konstrukcióját tűzve ki célul az ![]() térben. Az ilyen alakú függvényeket waveletnek, a rendszert generáló
térben. Az ilyen alakú függvényeket waveletnek, a rendszert generáló ![]() függvényt anya-waveleteknek nevezzük. Az első, folytonos (szakaszonként lineáris) függvényekből álló ortonormált wavelet-rendszert Strömberg konstruálta 1980-ban. Meyer 1985-ben
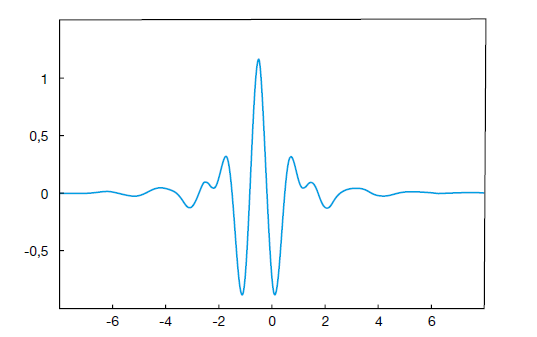
függvényt anya-waveleteknek nevezzük. Az első, folytonos (szakaszonként lineáris) függvényekből álló ortonormált wavelet-rendszert Strömberg konstruálta 1980-ban. Meyer 1985-ben ![]() -beli függvényekből álló ortonormált wavelet-bázisoknak egy osztályát adta meg, explicit módon előállítva az anya-waveletet (kompakt tartójú) Fourier-transzformáltját [3]. A bevezetőben bemutatott ábra egy Meyer-wavelet grafikonját szemlélteti.
-beli függvényekből álló ortonormált wavelet-bázisoknak egy osztályát adta meg, explicit módon előállítva az anya-waveletet (kompakt tartójú) Fourier-transzformáltját [3]. A bevezetőben bemutatott ábra egy Meyer-wavelet grafikonját szemlélteti.
Waveletek szerkesztése, a Haar-rendszert kivéve, nehéz feladatnak bizonyult. A konstrukciókban, a Meyer-féle wavelethez hasonlóan, a ![]() anya-wavelet helyett annak
anya-wavelet helyett annak ![]() Fourier-transzformációjából célszerű kiindulni. A továbbiakban az
Fourier-transzformációjából célszerű kiindulni. A továbbiakban az ![]() -beli függvény Fourier-transzformáltját, az
-beli függvény Fourier-transzformáltját, az ![]() (
( ![]() ) függvényeket alapul véve,
) függvényeket alapul véve, ![]() szerint értelmezzük és terjesztjük ki az
szerint értelmezzük és terjesztjük ki az ![]() térre. Annak ellenére, hogy maga a
térre. Annak ellenére, hogy maga a ![]() általában nem adható meg explicit alakban, a wavelet Fourier-sorok jó konvergencia- és approximációs tulajdonságokkal rendelkeznek, a sorfejtés részletösszegeinek magfüggvényei jól becsülhetők és a wavelet Fourier-együtthatók hatékony algoritmussal számíthatók.
általában nem adható meg explicit alakban, a wavelet Fourier-sorok jó konvergencia- és approximációs tulajdonságokkal rendelkeznek, a sorfejtés részletösszegeinek magfüggvényei jól becsülhetők és a wavelet Fourier-együtthatók hatékony algoritmussal számíthatók.
Különösen hasznosnak bizonyultak a sima, kompakt tartójú waveletek, amelyek Ingrid Daubechies úttörő munkásságanak köszönhetően nemcsak az elméletben, hanem a gyakorlati alkalmazásokban is központi szerepet játszanak [3]. Az említett két tulajdonság egymás ellen hat: minél rövidebb a wavelet tartója, annál kisebb a simaságát jellemző Hölder-kitevő. A Daubechies által bevezetett, az ![]() paramétertől függő
paramétertől függő ![]() wavelet tartójának hossza
wavelet tartójának hossza ![]() és Hölder-folytonos:
és Hölder-folytonos: ![]() (
( ![]() ). A waveletek konstrukciójában fontos szerepet játszik a
). A waveletek konstrukciójában fontos szerepet játszik a ![]() anya-wavelettel szoros kapcsolatban álló skálázási függvény vagy apa-wavelet.
anya-wavelettel szoros kapcsolatban álló skálázási függvény vagy apa-wavelet.
A skálázási függvény értelmezését és szerepét a Haar-rendszer példáján mutatjuk be. Ebben az esetben ![]() az anya-wavelet és a
az anya-wavelet és a ![]() intervallum
intervallum ![]() karakterisztikus függvénye az apa-wavelet. Legyen
karakterisztikus függvénye az apa-wavelet. Legyen ![]() (
( ![]() ,
, ![]() ) a
) a ![]() által generált wavelet-sorozat és jelölje
által generált wavelet-sorozat és jelölje ![]() a
a ![]() által generált zárt alteret az
által generált zárt alteret az ![]() térben. Nyilvánvaló, hogy
térben. Nyilvánvaló, hogy ![]() (
( ![]() ) és
) és ![]() mindenütt sűrű a
mindenütt sűrű a ![]() térben. Ebből következik, hogy a
térben. Ebből következik, hogy a ![]() ortogonális projekciókra
ortogonális projekciókra ![]() (
(![]() ,
, ![]() ) a
) a ![]() -tér normájában, a
-tér normájában, a ![]() (
( ![]() ) alterek egymásra ortogonálisak, továbbá a
) alterek egymásra ortogonálisak, továbbá a ![]() (
( ![]() ) Haar-rendszer egy ortonormált bázis ebben a térben, következésképpen a teljes
) Haar-rendszer egy ortonormált bázis ebben a térben, következésképpen a teljes ![]() (
( ![]() ) Haar-rendszer a
) Haar-rendszer a ![]() tér egy ortonormált bázisa.
tér egy ortonormált bázisa.
Ilyen típusú approximációs eljárást alkalmaztak jelek szűrésére (quadrature mirror filters) és képek tömörítésére (pyramid algorithms). Meyer ezeknek és az ehhez hasonló eljárásoknak tisztázta a matematikai hátterét, bevezetve a multirezolúciós analízis fogalmát. Jelölje ![]() az eltolás,
az eltolás, ![]() a dilatáció operátorát az
a dilatáció operátorát az ![]() -téren értelmezett függvények körében:
-téren értelmezett függvények körében: ![]() ,
, ![]() (
( ![]() ,
, ![]() ). A multirezolúció értelmezéséhez induljunk ki egy
). A multirezolúció értelmezéséhez induljunk ki egy ![]() függvényből, amelynek
függvényből, amelynek ![]() (
( ![]() ) eltoltjai Riesz-bázist alkotnak, más szóval létezik két konstans
) eltoltjai Riesz-bázist alkotnak, más szóval létezik két konstans ![]() , hogy bármely
, hogy bármely ![]() elem
elem ![]() normájára
normájára ![]() teljesül. Megjegyezzük, innen a
teljesül. Megjegyezzük, innen a ![]() speciális estben következik, hogy a
speciális estben következik, hogy a ![]() rendszer ortonormált. Az ilyen alakú Riesz-bázisok jellemezhetők a
rendszer ortonormált. Az ilyen alakú Riesz-bázisok jellemezhetők a ![]() Fourier-transzformáltjával, nevezetesen a
Fourier-transzformáltjával, nevezetesen a ![]() rendszer akkor és csak akkor Riesz-bázis, ha
rendszer akkor és csak akkor Riesz-bázis, ha ![]() , ahol
, ahol ![]() a periodizáló operátort jelöli:
a periodizáló operátort jelöli: ![]() (
( ![]() ). Ennek alapján szerkeszthetünk eltolás invariáns Riesz-bázisokat és ortonormált rendszereket. Mivel B-spline-ok Fourier-transzformáltja explicit alakban adható meg, azért ilyenekre a konstrukció egyszerűen elvégezhető.
). Ennek alapján szerkeszthetünk eltolás invariáns Riesz-bázisokat és ortonormált rendszereket. Mivel B-spline-ok Fourier-transzformáltja explicit alakban adható meg, azért ilyenekre a konstrukció egyszerűen elvégezhető.
Az ![]() (
( ![]() ) zárt altereknek egy monoton növő sorozatát multirezolúciónak nevezzük, ha i) uniójuk mindenütt sűrű
) zárt altereknek egy monoton növő sorozatát multirezolúciónak nevezzük, ha i) uniójuk mindenütt sűrű ![]() -ben, ii) metszetük a 0 függvényből álló triviális altér, iii)
-ben, ii) metszetük a 0 függvényből álló triviális altér, iii) ![]() bijekció, iv) az
bijekció, iv) az ![]() alteret egy
alteret egy ![]() alakú Riesz-bázis generálja.
alakú Riesz-bázis generálja.
A fenti értelmezéséből következik, hogy az ![]() teret generáló
teret generáló ![]() függvény meghatározza a multirezolúciót:
függvény meghatározza a multirezolúciót: ![]() a
a ![]() tér lezárása. Az
tér lezárása. Az ![]() (
( ![]() ) feltétel azzal ekvivalens, hogy
) feltétel azzal ekvivalens, hogy ![]() . Innen következik, hogy kompakt tartójú
. Innen következik, hogy kompakt tartójú ![]() esetén fennáll a
esetén fennáll a ![]() (
( ![]() ) ún. skálázási egyenlet. A
) ún. skálázási egyenlet. A ![]() wavelet konstansok ismeretében az egyenlet alapján iterációs eljárással meghatározhatjuk a
wavelet konstansok ismeretében az egyenlet alapján iterációs eljárással meghatározhatjuk a ![]() értékeit a diadikusan racionális pontokban [3]. Az alábbi ábrákon a skálázási függvények értékeit ilymódon számítottuk. A skálázási függvény (az apa-wavelet) ismeretében a
értékeit a diadikusan racionális pontokban [3]. Az alábbi ábrákon a skálázási függvények értékeit ilymódon számítottuk. A skálázási függvény (az apa-wavelet) ismeretében a ![]() anya-wavelet
anya-wavelet ![]() (
( ![]() ) alapján már meghatározható [3], [11], [15]. A Haar-rendszer esetén a skálázási egyenlet
) alapján már meghatározható [3], [11], [15]. A Haar-rendszer esetén a skálázási egyenlet ![]() és
és ![]() . Bármely
. Bármely ![]() -spline függvényre fennáll a skálázási egyenlet és az együtthatók explicit alakban adhatók meg.
-spline függvényre fennáll a skálázási egyenlet és az együtthatók explicit alakban adhatók meg.
Az alábbi ábrákon ![]() esetén szemléltetjük a Daubechies-féle skálázási függvényt és anya-waveletet.
esetén szemléltetjük a Daubechies-féle skálázási függvényt és anya-waveletet.
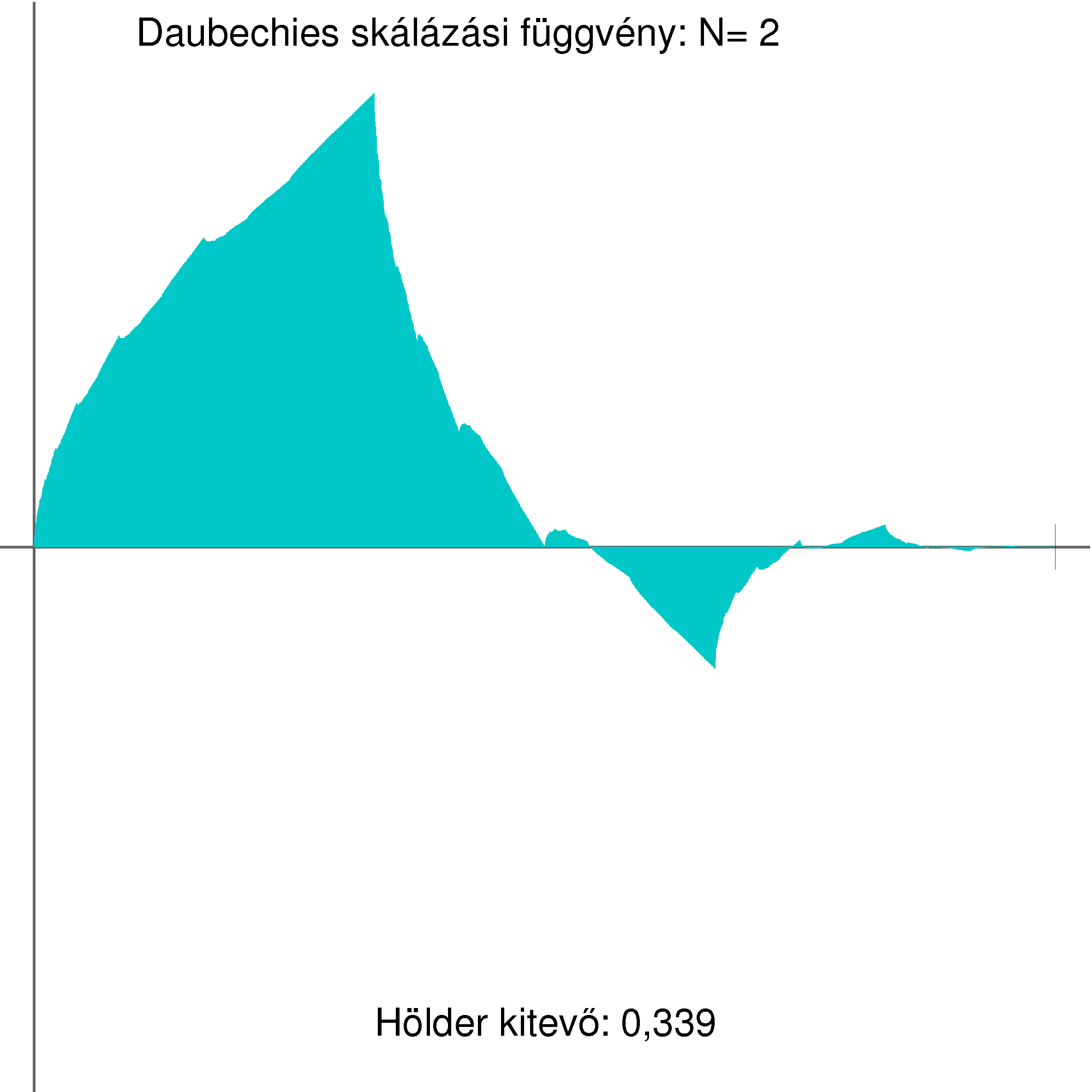
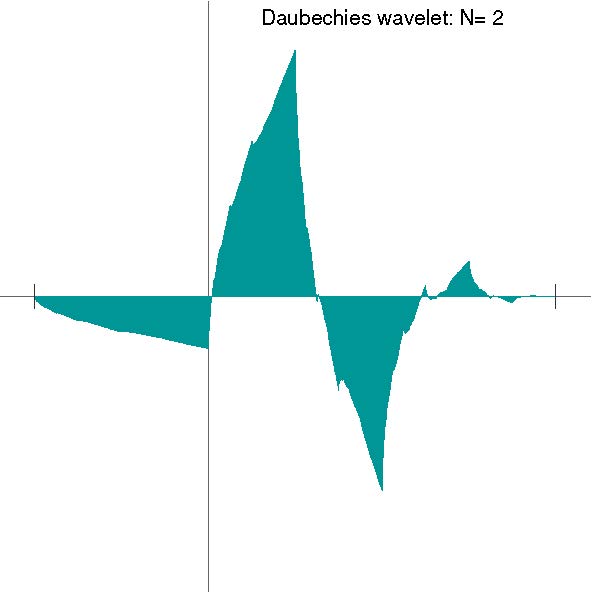
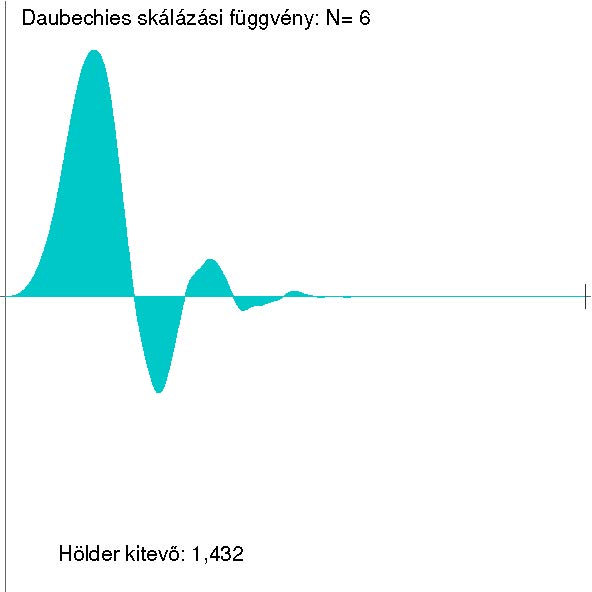
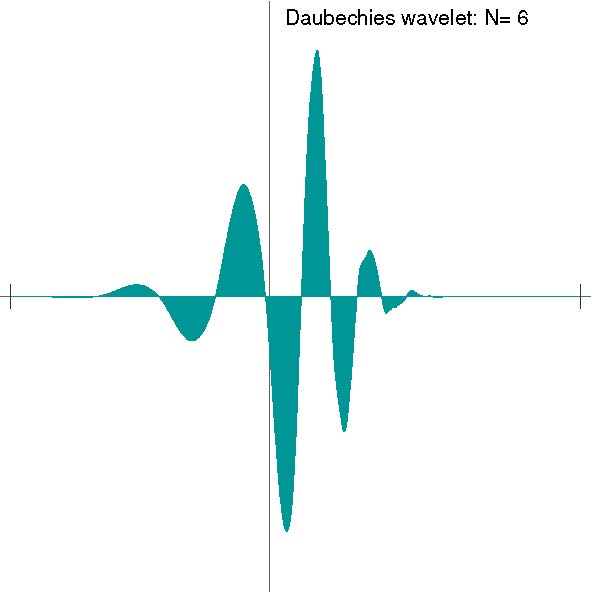
A skálázási egyenletet célszerű a Fourier-transzformáltakra (a frekvencia tartományban) felírni és megoldani. Kompakt tartójú skálázási függvény esetén ![]() (
( ![]() ), ahol az
), ahol az ![]() trigonometrikus polinomot, a jelfeldolgozásban szokásos terminológiát használva, a wavelet (alulvágó) szűrőjének nevezik. Bebizonyítható, hogy ha
trigonometrikus polinomot, a jelfeldolgozásban szokásos terminológiát használva, a wavelet (alulvágó) szűrőjének nevezik. Bebizonyítható, hogy ha ![]() MR-felbontást generál, akkor az 1-szerint periodikus
MR-felbontást generál, akkor az 1-szerint periodikus ![]() szűrőre
szűrőre ![]() ,
, ![]() (
( ![]() ) teljesül, továbbá
) teljesül, továbbá ![]() előállítható végtelen szorzatként:
előállítható végtelen szorzatként: ![]() . Megfordítva, kiindulva egy 1-szerint periodikus
. Megfordítva, kiindulva egy 1-szerint periodikus ![]() trigonometrikus polinomból, amely eleget tesz a
trigonometrikus polinomból, amely eleget tesz a ![]() feltételnek, a szóban forgó végtelen szorzat (kompakt intervallumokon egyenletesen) konvergál egy folytonos
feltételnek, a szóban forgó végtelen szorzat (kompakt intervallumokon egyenletesen) konvergál egy folytonos ![]() függvényhez. Amennyiben ezen kívül még
függvényhez. Amennyiben ezen kívül még ![]() teljesül, akkor a
teljesül, akkor a ![]() alapján számított
alapján számított ![]() MR-felbontást generál. Ez utóbbi feltétel biztosítására több elégséges feltétel ismert. Daubechies a (*) egyenletnek olyan
MR-felbontást generál. Ez utóbbi feltétel biztosítására több elégséges feltétel ismert. Daubechies a (*) egyenletnek olyan ![]() trigonometrikus polinom megoldásait határozta meg, amelyekből az említett módon származtatott
trigonometrikus polinom megoldásait határozta meg, amelyekből az említett módon származtatott ![]() skálázási függvény kompakt tartójú és
skálázási függvény kompakt tartójú és ![]() [3]. Megjegyezzük, hogy a konstrukcióban fontos szerepet játszik a következő Fejér-Riesz-féle tétel: Ha az
[3]. Megjegyezzük, hogy a konstrukcióban fontos szerepet játszik a következő Fejér-Riesz-féle tétel: Ha az ![]() páros trigonometrikus polinom nem-negatív, akkor van olyan
páros trigonometrikus polinom nem-negatív, akkor van olyan ![]() trigonometrikus polinom, amelyre
trigonometrikus polinom, amelyre ![]() (
( ![]() ).
).
Az utóbbi évtizedekben a waveletek számos változatát vezették be. Elsőként megemlítjük a waveletek egy folytonos paraméterektől függő osztályát, a ![]() (
(![]() ,
, ![]() ) waveleteket és az ezekkel képzett
) waveleteket és az ezekkel képzett ![]() (
(![]() ) transzformációkat, amelyeket Grossman és Morlet a kvantummechanika koherens állapotainak leírására vezetett be az 1980-as években. Kiderült, hogy az általuk felfedezett
) transzformációkat, amelyeket Grossman és Morlet a kvantummechanika koherens állapotainak leírására vezetett be az 1980-as években. Kiderült, hogy az általuk felfedezett ![]() (
( ![]() ) rekonstrukciós formula Calderon egy 20 évvel korábbi azonosságából következik. Ezek az eredmények késztették Meyert az ilyen típusú transzformációk szisztematikus vizsgálatára [5], [6].
) rekonstrukciós formula Calderon egy 20 évvel korábbi azonosságából következik. Ezek az eredmények késztették Meyert az ilyen típusú transzformációk szisztematikus vizsgálatára [5], [6].
A wavelet-transzformációk egy másik fontos osztályát, a Gábor Dénes által 1945-ben bevezetett (ablakos) Fourier-transzformációra utalva, Gábor-transzformációknak nevezik. Ebben az esetben az integráltranszformáció magfüggvénye egy ![]() ablakfüggvényből transzlációval és modulációval képzett
ablakfüggvényből transzlációval és modulációval képzett ![]() (
( ![]() ) függvénysereg, maga a transzformáció
) függvénysereg, maga a transzformáció ![]() (
(![]() ) alakú. A
) alakú. A ![]() függvényre tett megfelelő feltételek mellett mindkét esetben érvényesek a Fourier-transzformációra ismert, az energia-megmaradást kifejező, Plancherel-formula és a rekonstrukciót letővé tevő inverziós formula megfelelői.
függvényre tett megfelelő feltételek mellett mindkét esetben érvényesek a Fourier-transzformációra ismert, az energia-megmaradást kifejező, Plancherel-formula és a rekonstrukciót letővé tevő inverziós formula megfelelői.
Ezeknek a formuláknak az értelmezése, a Fourier-transzformálthoz hasonlóan, számos kérdést vet fel. Weisz Ferenc igen általános feltételek mellett, különböző konvergencia típusokat és szummációs eljárásokat alapul véve meghatározta a szóban forgó formulák érvényességi körét, messzemenően általánosítva a korábbi eredményeket [7], [16].
A Fourier-transzformációt az ![]() additív csoportjának
additív csoportjának ![]() (
( ![]() ) karakterei, az
) karakterei, az ![]() egydimenziós reprezentációi, segítségével értelmezzük:
egydimenziós reprezentációi, segítségével értelmezzük: ![]() . Az absztrakt harmonikus analízis szemléletét követve ezen az alapon a Fourier-transzformáció fontos tulajdonságai levezethetők. A wavelet- és a Gábor-transzformáció az
. Az absztrakt harmonikus analízis szemléletét követve ezen az alapon a Fourier-transzformáció fontos tulajdonságai levezethetők. A wavelet- és a Gábor-transzformáció az ![]() affin csoportjának, ill. a Heisenberg-féle csoport egy-egy reprezentációjából kiindulva hasonló elvek szerint származtatható. Ez a szemlélet elősegíti az említett transzformációk mélyebb megértését és mintát ad hasonló típusú leképezések szerkesztéséhez. A Bolyai-Lobacsevszkij-féle geometria egybevágósági transzformációiból kiindulva bevezettük a hiperbolikus waveleteket és az ezek által generált transzformációkat, valamint bebizonyítottuk a Plancherel- és a rekonstrukciós formulák megfelelőit [12]. Pap Margit a hiperbolikus waveletek diszkrét változatából kiindulva a
affin csoportjának, ill. a Heisenberg-féle csoport egy-egy reprezentációjából kiindulva hasonló elvek szerint származtatható. Ez a szemlélet elősegíti az említett transzformációk mélyebb megértését és mintát ad hasonló típusú leképezések szerkesztéséhez. A Bolyai-Lobacsevszkij-féle geometria egybevágósági transzformációiból kiindulva bevezettük a hiperbolikus waveleteket és az ezek által generált transzformációkat, valamint bebizonyítottuk a Plancherel- és a rekonstrukciós formulák megfelelőit [12]. Pap Margit a hiperbolikus waveletek diszkrét változatából kiindulva a ![]() Hardy-térnek egy multirezolúciós felbontását adta meg [8]. Racionális függvényekből álló waveleteket sikerrel alkalmaztunk EKG-görbék matematikai modellezésére és tömörítésére, valamint irányításelméleti problémák megoldására [1], [4].
Hardy-térnek egy multirezolúciós felbontását adta meg [8]. Racionális függvényekből álló waveleteket sikerrel alkalmaztunk EKG-görbék matematikai modellezésére és tömörítésére, valamint irányításelméleti problémák megoldására [1], [4].
A wavelet konstrukciók alapvető eszköze a Fourier-transzformáció. Ez az észrevétel inspirált bennünket arra, hogy alkalmas formában leírva a lokális testek Fourier-transzformációit lerakjuk a wavelet-konstrukcióhoz szükséges technikai alapokat [10].
Irodalomjegyzék
- 1
- J. BOKOR, F. SCHIPP, A. SOUMELIDIS: Applying hyperbolic wavelet construction in the identification of signals and systems. 15th IFAC Symposium on System Identification, SYSID 2009, Saint-Malo, France, July 6-8, 2009.
2- Z. CIESIELSKI: Haar orthogonal functions in analysis and probability. A. Haar memorial conference. Coll. Math. Soc. J. Bolyai, Eds. J. Szabados , K. Tandori, 49 (1985), pp. 27-56.
3- I. DAUBECHIES: Ten Lectures on Wavelets. SIAM, Philadelphia, Pennsylvania (1992).
4- S. FRIDLI, L. LÓCSI, F. SCHIPP: Rational Function Systems in ECG Processing. EUROCAST 2011, Springer LNCS 6927, 88-95.
5- Y. MEYER: Ondelettes et opérateurs. I. Ondelettes, II. Opérateurs de Calderon-Zygmund, III. Opérateurs multilinéaire. Hermann, Paris, 1990. English translation in Cambridge University Press (1992).
6- Y. MEYER: Wavelets. Algorithms and Applications. SIAM, Philadelphia, Pennsylvania (1992).
7- H. G. FEICHTINGER, F. WEISZ: Gabor analysis on Wiener amalgams. Sampl. Theory Signal Image Process. 6.129-150 (2007)
8- M. PAP: Hyperbolic Wavelets and Multiresolution in
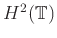 . Journal of Fourier Analysis and Applications, 2011, DOI: 10.1007/s00041-011-9169-2.
. Journal of Fourier Analysis and Applications, 2011, DOI: 10.1007/s00041-011-9169-2.
9- F. SCHIPP, W. R. WADE, P. SIMON, J. PÁL: Walsh series. An introduction to dyadic harmonic analysis. Akadémia Kiadó, Budapest, Adam Hilger, Bristol and New York (1990).
10- F. SCHIPP, W. R. WADE: Transforms on normed fields. Leaflets in Mathematics, Pécs (1995)
11- SCHIPP F.: Waveletek. Egyetemi jegyzet alkalmazott- és programtervező matematikusoknak, ELTE (2013). (http://numanal.inf.elte.hu/schipp)
12- SCHIPP F.: Hiperbolikus waveletek. Alkalmazott Matematikai Lapok 32 (2015), 1-40.
13- SZŐKEFALVI-NAGY B.: Függvények és függvénysorok. Polygon, Szeged (2002).
14- P. L. ULJANOV: Haar series and related questions. A. Haar memorial conference. Coll. Math. Soc. J. Bolyai, Eds. J. Szabados , K. Tandori, 49 (1985), pp. 57-96.
15- WEISZ F.: Wavelet- és Gábor-transzformált. ELTE, Budapest (2013), 317 pp. ISBN 978-963-284-453-4
16- F. WEISZ: Multi-dimensional Summability Theory and Applications. Current Topics in Summability Theory and Application. Eds. H. Dutta and B. E. Rhoades, Springer Singapore, 2016, 241-311.
Schipp Ferenc
professor emeritus
ELTE Infomatikai Kar, Numerikus Analízis Tanszék









