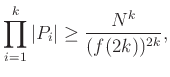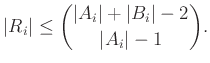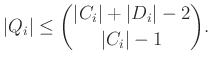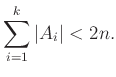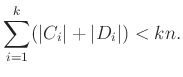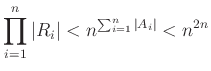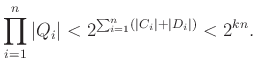1. Konvex sokszögek
Egy véges síkbeli ![]() ponthalmazt konvex helyzetűnek nevezünk, ha mindegyik pontja elválasztható a többitől egy egyenessel, azaz bármelyik
ponthalmazt konvex helyzetűnek nevezünk, ha mindegyik pontja elválasztható a többitől egy egyenessel, azaz bármelyik ![]() ponthoz található olyan egyenes, melynek
ponthoz található olyan egyenes, melynek ![]() az egyik, míg
az egyik, míg ![]() többi pontja a másik oldalán van. Eszerint egy legfeljebb két pontú ponthalmaz mindig konvex helyzetben van, a legalább három pontú ponthalmazok közül éppen a konvex sokszögek csúcshalmazai vannak konvex helyzetben. Így egy egyenes pontjai között sosem találunk hármat konvex helyzetben. Hogy ezt a problémát elkerüljük, a továbbiakban csak általános helyzetű ponthalmazokkal foglalkozunk, azaz feltesszük, hogy a pontok közt nincs három egy egyenesen.
többi pontja a másik oldalán van. Eszerint egy legfeljebb két pontú ponthalmaz mindig konvex helyzetben van, a legalább három pontú ponthalmazok közül éppen a konvex sokszögek csúcshalmazai vannak konvex helyzetben. Így egy egyenes pontjai között sosem találunk hármat konvex helyzetben. Hogy ezt a problémát elkerüljük, a továbbiakban csak általános helyzetű ponthalmazokkal foglalkozunk, azaz feltesszük, hogy a pontok közt nincs három egy egyenesen.

Klein Eszter, az akkor 22 éves egyetemista 1932-ben vette észre, hogy öt általános helyzetű pont között a síkon mindig van négy, ami konvex helyzetben van. A bizonyítás nagyon egyszerű. Ha a pontok konvex burka (a legnagyobb sokszög, amit meghatároznak) ötszög vagy négyszög, akkor az állítás nyilvánvaló. Ha a konvex burok egy ![]() háromszög, akkor további két pont,
háromszög, akkor további két pont, ![]() és
és ![]() , ennek a belsejében van. A
, ennek a belsejében van. A ![]() egyenes az
egyenes az ![]() háromszög két oldalát metszi, mondjuk
háromszög két oldalát metszi, mondjuk ![]() -t és
-t és ![]() -t. Ekkor viszont
-t. Ekkor viszont ![]() ,
, ![]() ,
, ![]() és
és ![]() konvex helyzetben van. Klein Eszter megkérdezte, hogy ez az egyszerű észrevétele általánosítható-e: vajon elég sok általános helyzetű pont között már feltétlenül találunk-e ötöt (hatot, stb.) konvex helyzetben? Tehát Klein Eszter kérdése a következő.
konvex helyzetben van. Klein Eszter megkérdezte, hogy ez az egyszerű észrevétele általánosítható-e: vajon elég sok általános helyzetű pont között már feltétlenül találunk-e ötöt (hatot, stb.) konvex helyzetben? Tehát Klein Eszter kérdése a következő.
Igaz-e, hogy minden ![]() természetes számhoz létezik egy
természetes számhoz létezik egy ![]() szám azzal a tulajdonsággal, hogy
szám azzal a tulajdonsággal, hogy ![]() általános helyzetű pont között a síkon mindig van
általános helyzetű pont között a síkon mindig van ![]() amelyek konvex helyzetben vannak.
amelyek konvex helyzetben vannak.
Érdekes meghatározni a legkisebb megfelelő ![]() számot, legyen tehát
számot, legyen tehát ![]() az a legkisebb
az a legkisebb ![]() egész szám, hogy
egész szám, hogy ![]() általános helyzetű pont közül a síkon mindig van
általános helyzetű pont közül a síkon mindig van ![]() konvex helyzetben. Ebben a megfogalmazásban Klein Eszter kérdése az, hogy létezik-e egyáltalán
konvex helyzetben. Ebben a megfogalmazásban Klein Eszter kérdése az, hogy létezik-e egyáltalán ![]() minden
minden ![]() -re.
-re.
Világos, hogy ![]() és az előbbi észrevétel alapján
és az előbbi észrevétel alapján ![]() . De egy háromszög három csúcsa és egy belső pontja mutatja, hogy négy általános helyzetű pont nem mindig van konvex helyzetben, tehát
. De egy háromszög három csúcsa és egy belső pontja mutatja, hogy négy általános helyzetű pont nem mindig van konvex helyzetben, tehát ![]() . Makai Endre és Turán Pál néhány héten belül belátták, hogy
. Makai Endre és Turán Pál néhány héten belül belátták, hogy ![]() [2], majd Szekeres György még abban az évben bebizonyította, hogy
[2], majd Szekeres György még abban az évben bebizonyította, hogy ![]() létezik minden
létezik minden ![]() -re. Természetesen adódott a következő kérdés:
-re. Természetesen adódott a következő kérdés:
Erdős—Szekeres probléma. Határozzuk meg ![]() értékét.
értékét.
Nem sokkal később Erdős alaposan megjavította Szekeres korlátját, majd közösen publikálták az eredményt [2], amely szerint minden ![]() -ra
-ra
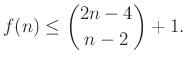
Sőt, ![]() ,
, ![]() és
és ![]() értékei alapján a következő merész sejtést is megfogalmazták:
értékei alapján a következő merész sejtést is megfogalmazták:
Sejtés. Minden ![]() -ra
-ra
Ez az egyszerű probléma, eredmény, illetve sejtés korszakalkotó jelentőségűnek bizonyult, egyfelől azért, mert hozzájárult F. P. Ramsey öt évvel korábban megjelent eredményeinek [13] újrafelfedezéséhez és ezzel a Ramsey-elmélet megalapozásához, másfelől azért is, mert megnyitotta az utat ponthalmazok kombinatorikájának tanulmányozásához, ami mára szép és gazdag területe lett a matematikának.
Klein Eszter és Szekeres György nem sokkal később összeházasodtak, ezért a problémát Erdős „Happy End Problem”-nek nevezte.
A legjobb ismert alsó korlát ![]() -re éppen a sejtett értéke,
-re éppen a sejtett értéke, ![]() , az ezt bizonyító konstrukciót Erdős és Szekeres találták 25 évvel később [3]. A konstrukció
, az ezt bizonyító konstrukciót Erdős és Szekeres találták 25 évvel később [3]. A konstrukció ![]() pontból áll és semelyik
pontból áll és semelyik ![]() pontja sincs konvex helyzetben. Nagyon szimmetrikus és „merev”, ha bármelyik pontját lényegesen elmozdítjuk, keletkezik
pontja sincs konvex helyzetben. Nagyon szimmetrikus és „merev”, ha bármelyik pontját lényegesen elmozdítjuk, keletkezik ![]() pont konvex helyzetben. Ezért a konstrukció alapján könnyen gondolhatja az ember, hogy nem javítható, vagyis a sejtés igaz.
pont konvex helyzetben. Ezért a konstrukció alapján könnyen gondolhatja az ember, hogy nem javítható, vagyis a sejtés igaz.
Erdős és Szekeres felső korlátja, ![]() , tehát majdnem a négyzete az alsó korlátnak. A problémával nagyon sokan foglalkoztak, szépsége és fontossága miatt, ennek ellenére a felső korlátot először 60 évvel később sikerült megjavítani. 1998-ban Fan Chung és Ron Graham [1] egy unalmas repülőúton azt vizsgálta, hogy ha az igazság pontosan a felső korlát lenne, tehát
, tehát majdnem a négyzete az alsó korlátnak. A problémával nagyon sokan foglalkoztak, szépsége és fontossága miatt, ennek ellenére a felső korlátot először 60 évvel később sikerült megjavítani. 1998-ban Fan Chung és Ron Graham [1] egy unalmas repülőúton azt vizsgálta, hogy ha az igazság pontosan a felső korlát lenne, tehát ![]() , akkor hogyan nézne ki egy
, akkor hogyan nézne ki egy ![]() elemű ponthalmaz, amiben még nincs konvex
elemű ponthalmaz, amiben még nincs konvex ![]() -szög. Belátták egy nagyon ügyes érveléssel, hogy ilyen ponthalmaz nem létezhet, és ezzel a felső korlátot a lehető legkisebb mértékben,
-szög. Belátták egy nagyon ügyes érveléssel, hogy ilyen ponthalmaz nem létezhet, és ezzel a felső korlátot a lehető legkisebb mértékben, ![]() -gyel megjavították. Ezen felbuzdulva Kleitman és Pachter [6] nagyjából egy hónappal később belátták, hogy
-gyel megjavították. Ezen felbuzdulva Kleitman és Pachter [6] nagyjából egy hónappal később belátták, hogy ![]() , tehát a javítás mértéke már tart a végtelenbe. Majd újabb egy hónap múlva Tóth és Valtr [16] belátták, hogy
, tehát a javítás mértéke már tart a végtelenbe. Majd újabb egy hónap múlva Tóth és Valtr [16] belátták, hogy ![]() , ami már nagyjából a fele az eredeti korátnak. Ez a három javítás időben olyan közel volt egymáshoz, hogy a Discrete and Computational Geometry című újságnak ugyanabban a számában jelentek meg. Itt leállt a javítások sorozata egy időre, és továbbra is óriasi volt az eltérés a felső és az alsó korát között. 2005-ben Tóth és Valtr [17] kombinálták a saját módszerüket Chung és Graham módszerével, így újra megjavították eggyel a felső korlátot.
, ami már nagyjából a fele az eredeti korátnak. Ez a három javítás időben olyan közel volt egymáshoz, hogy a Discrete and Computational Geometry című újságnak ugyanabban a számában jelentek meg. Itt leállt a javítások sorozata egy időre, és továbbra is óriasi volt az eltérés a felső és az alsó korát között. 2005-ben Tóth és Valtr [17] kombinálták a saját módszerüket Chung és Graham módszerével, így újra megjavították eggyel a felső korlátot.
2015-ben aztán újra megindult a lavina, Georgios Vlachos, egy MSc diák az MIT-ről, tovább javította a felső korlátot egy ![]() [15] faktorral. Hossein Mojarraddal közösen alaposan leegyszerűsítették és tökéletesítették a bizonyítást, végül a
[15] faktorral. Hossein Mojarraddal közösen alaposan leegyszerűsítették és tökéletesítették a bizonyítást, végül a ![]() faktor helyett egy
faktor helyett egy ![]() faktorral javítottak [7]. Közben Norin és Yuditsky [9] is elérték lényegében ugyanezt a korlátot, de még egyszerűbb bizonyítással.
faktorral javítottak [7]. Közben Norin és Yuditsky [9] is elérték lényegében ugyanezt a korlátot, de még egyszerűbb bizonyítással.
 Ezután jött az igazi áttörés, 2016-ban Andrew Suk (ld. a fotón) elképesztő javítással állt elő [14]. Több korábbi módszert, ötletet ügyesen kombinálva sikerült a felső korlátot levinnie az alsó korlát közelébe. Belátta, hogy
Ezután jött az igazi áttörés, 2016-ban Andrew Suk (ld. a fotón) elképesztő javítással állt elő [14]. Több korábbi módszert, ötletet ügyesen kombinálva sikerült a felső korlátot levinnie az alsó korlát közelébe. Belátta, hogy ![]() , ezzel kis híján megoldotta Klein, Erdős és Szekeres problémáját. Az elegáns bizonyítást Andreas Holmsen, Hossein Mojarrad, Pach János és Tardos Gábor tovább egyszerűsítette, és a korlátot is sikerült egy kicsit megjavítaniuk [5]. A pillanatnyilag ismert legjobb felső korlát
, ezzel kis híján megoldotta Klein, Erdős és Szekeres problémáját. Az elegáns bizonyítást Andreas Holmsen, Hossein Mojarrad, Pach János és Tardos Gábor tovább egyszerűsítette, és a korlátot is sikerült egy kicsit megjavítaniuk [5]. A pillanatnyilag ismert legjobb felső korlát ![]() -re az övék:
-re az övék:
Könnyebb áttekinteni a különböző korlátokat, ha nem a fenti ![]() függvényt, hanem az ekvivalens inverz problemát, és az alábbi
függvényt, hanem az ekvivalens inverz problemát, és az alábbi ![]() függvényt vizsgáljuk. Legyen
függvényt vizsgáljuk. Legyen ![]() az a legnagyobb
az a legnagyobb ![]() egész szám, amelyre
egész szám, amelyre ![]() általános helyzetű pont között a síkon mindig található
általános helyzetű pont között a síkon mindig található ![]() konvex helyzetben. Az Erdős—Szekeres sejtés ekvivalans azzal, hogy
konvex helyzetben. Az Erdős—Szekeres sejtés ekvivalans azzal, hogy
minden pozitív ![]() egészre. Itt, és a továbbiakban
egészre. Itt, és a továbbiakban ![]() a kettes alapú logaritmust jelöli. Az
a kettes alapú logaritmust jelöli. Az ![]() -re adott alsó és felső korlátok szerepe megfordul. Erdős és Szekeres 1935-ös felső korlátjából [2] alsó korlát lesz
-re adott alsó és felső korlátok szerepe megfordul. Erdős és Szekeres 1935-ös felső korlátjából [2] alsó korlát lesz ![]() -re, míg az 1961-es alsó korlátjukból [3]
-re, míg az 1961-es alsó korlátjukból [3] ![]() -re felső korlát adódik:
-re felső korlát adódik:
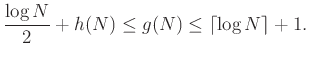
Itt ![]() egy aszimptotikusan
egy aszimptotikusan ![]() közeli függvény, ami az alsó becslés nagyságrendjét nem befolyásolja. Az
közeli függvény, ami az alsó becslés nagyságrendjét nem befolyásolja. Az ![]() -re adott alsó és felső becslés közötti majdnem négyzetes eltérésből a
-re adott alsó és felső becslés közötti majdnem négyzetes eltérésből a ![]() esetében egy majdnem kettes faktor eltérés marad. Chung és Graham [1] 1-gyel javította az
esetében egy majdnem kettes faktor eltérés marad. Chung és Graham [1] 1-gyel javította az ![]() -re adott felső becslést, ebből a
-re adott felső becslést, ebből a ![]() -re adott aló becslés javítása következik 1-gyel, de csak bizonyos (ritka)
-re adott aló becslés javítása következik 1-gyel, de csak bizonyos (ritka) ![]() értékekre. A további javítások [6,16,17,15,7,9] ugyancsak eggyel javították csak Erdős és Szekeres alsó becslését a
értékekre. A további javítások [6,16,17,15,7,9] ugyancsak eggyel javították csak Erdős és Szekeres alsó becslését a ![]() függvényre, de egyre több és több
függvényre, de egyre több és több ![]() érték esetén. Suk átütő eredménye [14] azonban aszimptotikusan bezárta az alsó és felső becslés közötti kettes faktor eltérést:
érték esetén. Suk átütő eredménye [14] azonban aszimptotikusan bezárta az alsó és felső becslés közötti kettes faktor eltérést:
A hibatag nagyságrendjét [5] tovább csökkenti ![]() -re.
-re.
Az eddig tárgyalt becslések nem segítettek abban, hogy az ![]() értéket minél több (kicsi)
értéket minél több (kicsi) ![]() értékre meghatározzuk. Említettük, hogy Klein Eszter 1932-ben belátta, hogy
értékre meghatározzuk. Említettük, hogy Klein Eszter 1932-ben belátta, hogy ![]() , valamint hogy Makai és Turán ugyanakkor belátták, hogy
, valamint hogy Makai és Turán ugyanakkor belátták, hogy ![]() . Szekeres György bő hetven év elteltével visszatért a problémához és Lindsay Petersszel közös publikációban [12] belátták, hogy
. Szekeres György bő hetven év elteltével visszatért a problémához és Lindsay Petersszel közös publikációban [12] belátták, hogy ![]() . Ez az eredmény komolyabb komputeres esetvizsgálaton alapul és már Szekeres halála után jelent meg. Az
. Ez az eredmény komolyabb komputeres esetvizsgálaton alapul és már Szekeres halála után jelent meg. Az ![]() érték semmilyen
érték semmilyen ![]() számra nem ismert.
számra nem ismert.
Ebben a cikkben áttekintjük az alsó korlát konstrukciót, a felső korlát javításait, a felhasznált módszereket, és vázoljuk a legjobb ismert korlát bizonyítását.
Az Erdős—Szekeres problémának számos általánosítását, módosítását vizsgálták, sok izgalmas és szép eredménnyel. Ezekről ad kiváló összefoglalót magyarul Pach János [10], angolul Morris és Soltan [8]. Suk eredményéről nagyon szórakoztató ismeretterjesztő cikket írt Hartnett [4].
2. Hegyek és völgyek
Szekeres legelső bizonyítása [2] ![]() létezésére a Ramsey tételt használta, amit újra bebizonyított, mert nem ismerte Ramsey publikációját. Erdős javítása, [2] és az összes további javítás legfontosabb segédeszközei a hegyek és völgyek.
létezésére a Ramsey tételt használta, amit újra bebizonyított, mert nem ismerte Ramsey publikációját. Erdős javítása, [2] és az összes további javítás legfontosabb segédeszközei a hegyek és völgyek.
Definíció. Rögzítsünk egy ![]() koordinátarendszert a síkon. Ezentúl egy ponthalmazra akkor mondjuk, hogy általános helyzetű, ha nincs három pontja egy egyenesen és nem egyezik meg két pontjának az
koordinátarendszert a síkon. Ezentúl egy ponthalmazra akkor mondjuk, hogy általános helyzetű, ha nincs három pontja egy egyenesen és nem egyezik meg két pontjának az ![]() -koordinátája. Legyen
-koordinátája. Legyen ![]() és legyenek
és legyenek ![]() ,
, ![]() ,
, ![]() általános helyzetű pontok, balról jobbra, vagyis növekvő
általános helyzetű pontok, balról jobbra, vagyis növekvő ![]() -koordináta szerint rendezve. A
-koordináta szerint rendezve. A ![]() pontok egy
pontok egy ![]() -hegyet (
-hegyet (![]() -völgyet) alkotnak, ha konvex helyzetben vannak és
-völgyet) alkotnak, ha konvex helyzetben vannak és ![]() ,
, ![]() a
a ![]() egyenes fölött (alatt) van (2. ábra).
egyenes fölött (alatt) van (2. ábra).
A ![]() -völgyek, illetve
-völgyek, illetve ![]() -hegyek
-hegyek ![]() esetén speciális konvex
esetén speciális konvex ![]() -szögek. Vegyük észre, hogy három általános helyzetű pont vagy 3-hegyet, vagy 3-völgyet alkot. Erdős és Szekeres bizonyításának alapja a következő észrevétel.
-szögek. Vegyük észre, hogy három általános helyzetű pont vagy 3-hegyet, vagy 3-völgyet alkot. Erdős és Szekeres bizonyításának alapja a következő észrevétel.
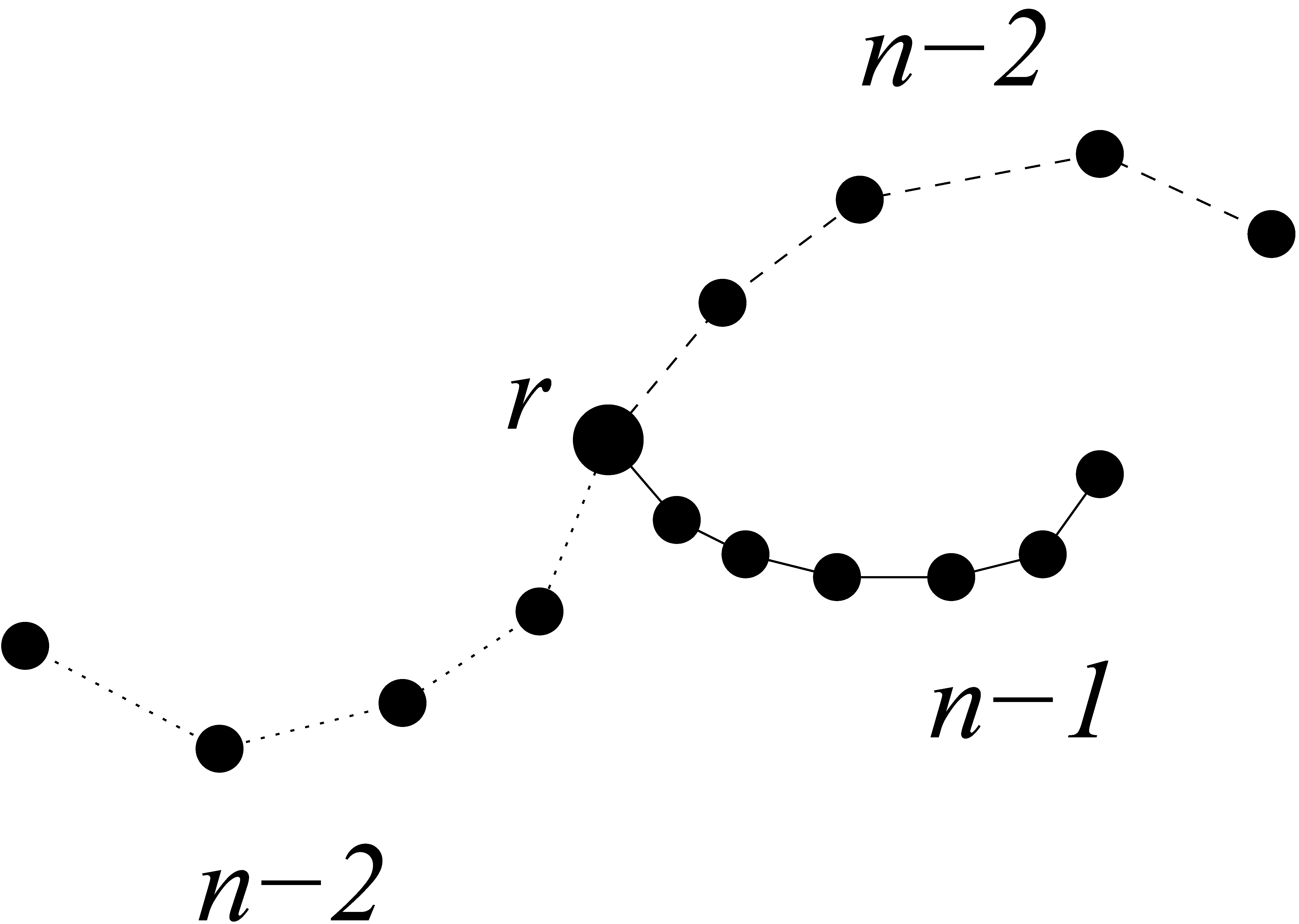
Ha egy ![]() -hegy utolsó pontja és egy
-hegy utolsó pontja és egy ![]() -völgy első pontja megegyezik, akkor valamelyiket egy ponttal meg lehet hosszabbítani.
-völgy első pontja megegyezik, akkor valamelyiket egy ponttal meg lehet hosszabbítani.
Valóban, legyen ![]() a
a ![]() -hegy utolsó pontja és az
-hegy utolsó pontja és az ![]() -völgy első pontja, legyen
-völgy első pontja, legyen ![]() a
a ![]() -hegy utolsó előtti pontja és legyen
-hegy utolsó előtti pontja és legyen ![]() az
az ![]() -völgy második pontja. Ekkor
-völgy második pontja. Ekkor ![]() vagy hegyet, vagy völgyet alkot. Az első esetben
vagy hegyet, vagy völgyet alkot. Az első esetben ![]() -rel kiegészíthetjük a hegyet egy
-rel kiegészíthetjük a hegyet egy ![]() -heggyé, a második esetben pedig a völgyet egészíthetjük ki
-heggyé, a második esetben pedig a völgyet egészíthetjük ki ![]() -val egy
-val egy ![]() -völggyé (2. ábra).
-völggyé (2. ábra).
Minden ![]() -re legyen
-re legyen ![]() az a legkisebb
az a legkisebb ![]() szám, amelyre igaz, hogy
szám, amelyre igaz, hogy ![]() általános helyzetű pont között a síkon mindig van egy
általános helyzetű pont között a síkon mindig van egy ![]() -hegy vagy egy
-hegy vagy egy ![]() -völgy. Nyilván
-völgy. Nyilván ![]() , ezért az alábbi tételből azonnal következik Erdős és Szekeres korlátja
, ezért az alábbi tételből azonnal következik Erdős és Szekeres korlátja ![]() -re. (Kicsit zavaró, hogy az „általános helyzet” fogalmát szigorítottuk, így elsőre csak az ilyen szigorúbb értelemben vett általános helyzetű
-re. (Kicsit zavaró, hogy az „általános helyzet” fogalmát szigorítottuk, így elsőre csak az ilyen szigorúbb értelemben vett általános helyzetű ![]() méretű síkbeli ponthalmazra adódik, hogy kiválasztható belőle
méretű síkbeli ponthalmazra adódik, hogy kiválasztható belőle ![]() konvex helyzetű pont. Ez a probléma kezelhető azzal, hogy az
konvex helyzetű pont. Ez a probléma kezelhető azzal, hogy az ![]() koordinátarendszert úgy választjuk, hogy ne legyen két pontnak azonos az
koordinátarendszert úgy választjuk, hogy ne legyen két pontnak azonos az ![]() koordinátája.) Meglepő módon,
koordinátája.) Meglepő módon, ![]() -nel ellentétben,
-nel ellentétben, ![]() értéket pontosan tudjuk.
értéket pontosan tudjuk.
1. Tétel. [2]
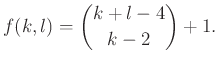
Bizonyítás. Először belátjuk, hogy minden ![]() -ra
-ra
Tekintsünk egy ![]() elemű általános helyzetű
elemű általános helyzetű ![]() ponthalmazt. Belátjuk, hogy mindenképpen tartalmaz
ponthalmazt. Belátjuk, hogy mindenképpen tartalmaz ![]() -hegyet vagy
-hegyet vagy ![]() -völgyet. Legyen
-völgyet. Legyen ![]() a
a ![]() -ben található
-ben található ![]() -hegyek utolsó pontjainak a halmaza. Ha
-hegyek utolsó pontjainak a halmaza. Ha ![]() , akkor
, akkor ![]() vagy tartalmaz egy
vagy tartalmaz egy ![]() -hegyet, és készen vagyunk, vagy egy
-hegyet, és készen vagyunk, vagy egy ![]() -völgyet. De ekkor ennek az
-völgyet. De ekkor ennek az ![]() -völgynek az első pontja egyben egy
-völgynek az első pontja egyben egy ![]() -hegy utolsó pontja is, tehát vagy a hegy, vagy a völgy meghosszabbítható és megint készen vagyunk. Vagyis feltehetjük, hogy
-hegy utolsó pontja is, tehát vagy a hegy, vagy a völgy meghosszabbítható és megint készen vagyunk. Vagyis feltehetjük, hogy ![]() , ekkor viszont
, ekkor viszont ![]() , tehát
, tehát ![]() tartalmaz egy
tartalmaz egy ![]() -völgyet és ismét készen vagyunk, vagy egy
-völgyet és ismét készen vagyunk, vagy egy ![]() -hegyet, ami ellentmondás, mert ennek az utolsó pontja
-hegyet, ami ellentmondás, mert ennek az utolsó pontja ![]() -hoz tartozna.
-hoz tartozna.
Legyen ![]() . Könnyű ellenőrizni, hogy
. Könnyű ellenőrizni, hogy
Ezenkívül ha ![]() vagy
vagy ![]() , akkor
, akkor ![]() . Ezekből pedig indukcióval adódik, hogy minden
. Ezekből pedig indukcióval adódik, hogy minden ![]() -re
-re ![]() .
.
Az alsó korláthoz minden ![]() -re konstruálunk egy
-re konstruálunk egy ![]() ponthalmazt, amely éppen
ponthalmazt, amely éppen ![]() pontból áll és nem tartalmaz
pontból áll és nem tartalmaz ![]() -hegyet és
-hegyet és ![]() -völgyet. A
-völgyet. A ![]() , illetve
, illetve ![]() esetben egy egy pontból álló halmaz jó lesz. Tegyük fel, hogy már megkonstruáltuk a
esetben egy egy pontból álló halmaz jó lesz. Tegyük fel, hogy már megkonstruáltuk a ![]() és a
és a ![]() ponthalmazokat. Helyezzük el őket egymás mellé úgy, hogy
ponthalmazokat. Helyezzük el őket egymás mellé úgy, hogy ![]() az
az ![]() -tengelytől balra,
-tengelytől balra, ![]() pedig jobbra legyen,
pedig jobbra legyen, ![]() minden pontja a
minden pontja a ![]() pontjai által meghatározott egyenesek fölött legyen, és
pontjai által meghatározott egyenesek fölött legyen, és ![]() minden pontja a
minden pontja a ![]() pontjai által meghatározott egyenesek alatt legyen. Az utóbbi két feltétel biztosítható azzal, ha a
pontjai által meghatározott egyenesek alatt legyen. Az utóbbi két feltétel biztosítható azzal, ha a ![]() ponthalmazt az
ponthalmazt az ![]() -tengellyel párhuzamosan megfelelő magasra toljuk. Ekkor minden
-tengellyel párhuzamosan megfelelő magasra toljuk. Ekkor minden ![]() -beli hegy maximum egy
-beli hegy maximum egy ![]() -beli ponttal egészíthető ki, és fordítva, minden
-beli ponttal egészíthető ki, és fordítva, minden ![]() -beli völgy maximum egy
-beli völgy maximum egy ![]() -beli ponttal egészíthető ki. Ebből adódik, hogy az így kapott
-beli ponttal egészíthető ki. Ebből adódik, hogy az így kapott ![]() elemű
elemű ![]() halmaz nem tartalmaz sem
halmaz nem tartalmaz sem ![]() -hegyet, sem
-hegyet, sem ![]() -völgyet.
-völgyet. ![]()
Vegyük észre, hogy ha ![]() pont konvex helyzetben van, akkor felbontható két részhalmaz úniójára, amiből az egyik hegy, a másik völgy. A hegy a konvex
pont konvex helyzetben van, akkor felbontható két részhalmaz úniójára, amiből az egyik hegy, a másik völgy. A hegy a konvex ![]() -szög „teteje”, a völgy az „alja” lesz. Ha feltesszük, hogy a pontok
-szög „teteje”, a völgy az „alja” lesz. Ha feltesszük, hogy a pontok ![]() -koordinátája páronként különböző, akkor a hegynek és a völgynek két közös pontja is lesz: a legkisebb és legnagyobb
-koordinátája páronként különböző, akkor a hegynek és a völgynek két közös pontja is lesz: a legkisebb és legnagyobb ![]() -koordinátájú csúcsa a konvex
-koordinátájú csúcsa a konvex ![]() -szögnek. Láttuk, hogy
-szögnek. Láttuk, hogy ![]() általános helyzetű pont közül mindig kiválaszthatunk
általános helyzetű pont közül mindig kiválaszthatunk ![]() -et konvex helyzetben: egy
-et konvex helyzetben: egy ![]() -hegyet, vagy egy
-hegyet, vagy egy ![]() völgyet. Találhatunk viszont
völgyet. Találhatunk viszont ![]() pontot általános helyzetben, hogy nincs köztük sem
pontot általános helyzetben, hogy nincs köztük sem ![]() -hegy, sem
-hegy, sem ![]() -völgy. Egy ilyen ponthalmaz nem tartalmaz
-völgy. Egy ilyen ponthalmaz nem tartalmaz ![]() pontot konvex pozicióban, hiszen az ellentmondana a fentebbi felbontásnak hegyre és völgyre.
pontot konvex pozicióban, hiszen az ellentmondana a fentebbi felbontásnak hegyre és völgyre.
Ez a gondolatmenet jól mutatja, hogy ![]() értékere (ez a legnagyobb
értékere (ez a legnagyobb ![]() szám, hogy
szám, hogy ![]() általános helyzetű pontból mindig kiválasztható
általános helyzetű pontból mindig kiválasztható ![]() konvex helyzetben) Erdős és Szekeres által adott alsó és felső becslések között miért körülbelül egy kettes faktor differencia van: Pontosan tudjuk, hogy mekkora hegy vagy völgy választható ki
konvex helyzetben) Erdős és Szekeres által adott alsó és felső becslések között miért körülbelül egy kettes faktor differencia van: Pontosan tudjuk, hogy mekkora hegy vagy völgy választható ki ![]() általános helyzetű pont közül, de azt már nehezebb meghatározni, hogy ezek mikor „illeszthetőek össze” egy konvex ponthalmazzá.
általános helyzetű pont közül, de azt már nehezebb meghatározni, hogy ezek mikor „illeszthetőek össze” egy konvex ponthalmazzá.
A fenti gondolatmenetet direktben is használhatjuk arra, hogy ![]() -re alső becslést adjunk. Ha
-re alső becslést adjunk. Ha ![]() , akkor
, akkor ![]() , hiszen
, hiszen ![]() konvex helyzetű pont között van
konvex helyzetű pont között van ![]() -hegy vagy
-hegy vagy ![]() -völgy. A korábban megkonstruált
-völgy. A korábban megkonstruált ![]() ponthalmazok ügyes kombinálásával kissé erősebb alsó becslést kapunk, ami egyben megegyezik
ponthalmazok ügyes kombinálásával kissé erősebb alsó becslést kapunk, ami egyben megegyezik ![]() sejtett értékével is:
sejtett értékével is:
2. Tétel. [3]
Bizonyítás. Legyen ![]() . Minden
. Minden ![]() -re (
-re ( ![]() ) helyezzük el
) helyezzük el ![]() egy nagyon pici és nagyon lapos példányát az
egy nagyon pici és nagyon lapos példányát az ![]() pont közelébe úgy, hogy a pontjai által meghatározott egyenesek mind majdnem vizszintesek. Nevezzük ezeket blokkoknak. Mindez azért lehetséges, mert a
pont közelébe úgy, hogy a pontjai által meghatározott egyenesek mind majdnem vizszintesek. Nevezzük ezeket blokkoknak. Mindez azért lehetséges, mert a ![]() ponthalmazt szabadon eltolhatjuk, kicsinyíthetjük, sőt „lapíthatjuk” is (alkalmazhatunk affin transzformációt az
ponthalmazt szabadon eltolhatjuk, kicsinyíthetjük, sőt „lapíthatjuk” is (alkalmazhatunk affin transzformációt az ![]() -tengely irányában), mindez nem befolyásolja hogy mekkora hegyek és völgyek vannak a ponthalmazban. Legyen
-tengely irányában), mindez nem befolyásolja hogy mekkora hegyek és völgyek vannak a ponthalmazban. Legyen ![]() a kapott halmaz. Világos, hogy
a kapott halmaz. Világos, hogy
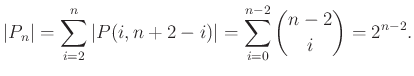
Azt állítjuk, hogy ![]() nem tartalmaz konvex
nem tartalmaz konvex ![]() -szöget. Legyen
-szöget. Legyen ![]() egy konvex ponthalmaz
egy konvex ponthalmaz ![]() -ben. Legyen
-ben. Legyen ![]() a legalsó blokk, amiben
a legalsó blokk, amiben ![]() -nak van pontja, és
-nak van pontja, és ![]() a legfelső. Ha
a legfelső. Ha ![]() , akkor
, akkor ![]() a
a ![]() blokk része, így a tétel kimondása előtti gondolatmenet alapján
blokk része, így a tétel kimondása előtti gondolatmenet alapján ![]() . Ha viszont
. Ha viszont ![]() , akkor
, akkor ![]()
![]() -ből egy völgyet tartalmaz, amelynek a mérete legfeljebb
-ből egy völgyet tartalmaz, amelynek a mérete legfeljebb ![]() ,
, ![]() -ből egy hegyet, aminek a mérete legfeljebb
-ből egy hegyet, aminek a mérete legfeljebb ![]() , és a köztük levő
, és a köztük levő ![]() blokk mindegyikéből legfeljebb egy pontot.
blokk mindegyikéből legfeljebb egy pontot.
Ezért ![]() .
. ![]()
3. Javítások
Mint említettük, az első javítást Chung és Graham érte el 1998-ban, [1]. Azt látták be, hogy ![]() . Tekintsünk egy
. Tekintsünk egy ![]() méretű ponthalmazt. Ha tartalmaz egy
méretű ponthalmazt. Ha tartalmaz egy ![]() -hegyet vagy
-hegyet vagy ![]() -völgyet, akkor készen vagyunk. Ha nem, akkor viszont Chung és Graham megmutatják, hogy található egy
-völgyet, akkor készen vagyunk. Ha nem, akkor viszont Chung és Graham megmutatják, hogy található egy ![]() -hegy és „alatta” egy pont, vagy egy
-hegy és „alatta” egy pont, vagy egy ![]() -völgy és „fölötte” egy pont, ami egy konvex
-völgy és „fölötte” egy pont, ami egy konvex ![]() -szöget alkot.
-szöget alkot.
A következő javítás Kleitman és Pachter eredménye, [6]. Észrevették, hogy az Erdős—Szekeres-féle hegyes-völgyes bizonyítás tetszőleges ![]() koordinátarendszerben elmondható. Úgy forgatták el a koordinátarendszert, hogy a konvex burok egyik éle függőleges legyen, és ezt a szakaszt „duplán” használták. Kiterjesztették a hegy és a völgy definícióját úgy, hogy ez a függőleges él lehet egy hegynek és egy völgynek is az utolsó éle. Ezzel egy kicsit jobb rekurziót kaptak, és azt, hogy
koordinátarendszerben elmondható. Úgy forgatták el a koordinátarendszert, hogy a konvex burok egyik éle függőleges legyen, és ezt a szakaszt „duplán” használták. Kiterjesztették a hegy és a völgy definícióját úgy, hogy ez a függőleges él lehet egy hegynek és egy völgynek is az utolsó éle. Ezzel egy kicsit jobb rekurziót kaptak, és azt, hogy ![]() .
.
Ezután következett Tóth és Valtr javítása, [16]. A módszerük lényege az, hogy a forgatásnál sokkal általánosabb transzformációt alkalmaznak a hegy-völgy érvelés előtt, mégpedig egy alkalmas projektív transzformációt. Tóth és Valtr azt látták be, hogy ![]() . Legyen
. Legyen ![]() egy
egy ![]() elemű ponthalmaz és
elemű ponthalmaz és ![]() a konvex burok egy csúcsa. Legyen
a konvex burok egy csúcsa. Legyen ![]() . Legyen
. Legyen ![]() egy
egy ![]() -t tartalmazó egyenes, amelynek
-t tartalmazó egyenes, amelynek ![]() minden pontja ugyanazon az oldalán van. Alkalmazzunk egy projektív transzformációt, amely
minden pontja ugyanazon az oldalán van. Alkalmazzunk egy projektív transzformációt, amely ![]() -et a végtelen távoli egyenesbe viszi,
-et a végtelen távoli egyenesbe viszi, ![]() -t az
-t az ![]() végtelen távoli pontba,
végtelen távoli pontba, ![]() -t pedig az
-t pedig az ![]() halmazba. Mivel
halmazba. Mivel ![]() ,
, ![]() tartalmaz egy
tartalmaz egy ![]() -hegyet vagy egy
-hegyet vagy egy ![]() -völgyet. Ha
-völgyet. Ha ![]() -völgyet tartalmaz, akkor könnyen látható, hogy a megfelelő pontok
-völgyet tartalmaz, akkor könnyen látható, hogy a megfelelő pontok ![]() -ban is konvex helyzetben vannak. Ha
-ban is konvex helyzetben vannak. Ha ![]() -hegyet tartalmaz, akkor pedig a megfelelő pontok és
-hegyet tartalmaz, akkor pedig a megfelelő pontok és ![]() együtt is konvex helyzetben vannak. Tehát kész vagyunk.
együtt is konvex helyzetben vannak. Tehát kész vagyunk.
A következő javítás nem túl izgalmas, ugyancsak Tóth és Valtr, [17], a fenti ![]() halmazra hasonlóan érvelt, mint Chung és Graham, így újból 1-et faragtak a korlátból.
halmazra hasonlóan érvelt, mint Chung és Graham, így újból 1-et faragtak a korlátból.
További tíz évvel később Georgios Vlachos következett, [15]. Gondolatmenete úgy indul, mint Tóth és Valtr bizonyítása: Legyen ![]() egy ponthalmaz, amely nem tartalmaz
egy ponthalmaz, amely nem tartalmaz ![]() pontot konvex helyzetben és legyen
pontot konvex helyzetben és legyen ![]() egy pontja a konvex burkon. Legyen
egy pontja a konvex burkon. Legyen ![]() . Legyen
. Legyen ![]() egy
egy ![]() -t tartalmazó egyenes, amelynek
-t tartalmazó egyenes, amelynek ![]() minden pontja ugyanazon az oldalán van. Alkalmazzunk egy projektív transzformációt, amely
minden pontja ugyanazon az oldalán van. Alkalmazzunk egy projektív transzformációt, amely ![]() -et a végtelen távoli egyenesbe viszi,
-et a végtelen távoli egyenesbe viszi, ![]() -t az
-t az ![]() végtelen távoli pontba,
végtelen távoli pontba, ![]() -t pedig az
-t pedig az ![]() halmazba.
halmazba.
Az eddigiek alapján megállapíthatjuk, hogy ![]() nem tartalmaz
nem tartalmaz ![]() -hegyet és
-hegyet és ![]() -völgyet. Sőt, nem tartalmaz olyan
-völgyet. Sőt, nem tartalmaz olyan ![]() pontot, amely egyszerre végpontja egy
pontot, amely egyszerre végpontja egy ![]() -völgynek és kezdőpontja egy
-völgynek és kezdőpontja egy ![]() -hegynek.
-hegynek.
Vlachos egy ennél bonyolultabb tiltott konfigurációt talált.
3. Lemma [15] Tegyük fel, hogy az ![]() ponthalmaz tartalmaz egy
ponthalmaz tartalmaz egy ![]() pontot, amely (1) egy
pontot, amely (1) egy ![]() -völgy végpontja, (2) egy
-völgy végpontja, (2) egy ![]() -hegy kezdőpontja, (3) egy
-hegy kezdőpontja, (3) egy ![]() -völgy kezdőpontja, és az
-völgy kezdőpontja, és az ![]() -völgy végpotja nem esik egybe az
-völgy végpotja nem esik egybe az ![]() -hegy második pontjával.
-hegy második pontjával.
Ekkor ![]() tartalmaz egy
tartalmaz egy ![]() -hegyet vagy
-hegyet vagy ![]() pontot konvex helyzetben, következésépp
pontot konvex helyzetben, következésépp ![]() tartalmaz
tartalmaz ![]() pontot konvex helyzetben.
pontot konvex helyzetben.
Ez a bonyolult tiltott konfiguráció egy jobb rekurzióra adott lehetőséget, mint az eredeti, Vlachos ennek felhasználásával azt kapta, hogy
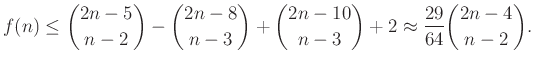
A gondolatmenetet tovább finomitották és egyszerűsítették Hossein Mojarraddal [7], es azt kapták, hogy
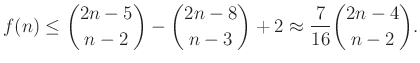
Norin és Yuditsky [9] is ezt a tiltott konfigurációt használták, a korlátjuk lényegében ugyanennyi, sőt, valamivel gyengébb, de az ő érvelésük nagyon egyszerű, impozáns, és remekül rámutat arra, hogy az új tiltott konfiguráció miért ad jobb korlátot. Nagyon élvezetes olvasmány.
4. Suk áttörése
Sok konvex ![]() -szög
-szög
Legyen ![]() es legyen
es legyen ![]() egy konvex
egy konvex ![]() -szög. Legyen
-szög. Legyen ![]()
![]() csúcsainak halmaza egy fix körüljárás szerint felsorolva. Tehát
csúcsainak halmaza egy fix körüljárás szerint felsorolva. Tehát ![]() konvex helyzetben van. Tekintsük a sík azon
konvex helyzetben van. Tekintsük a sík azon ![]() pontjait, amire
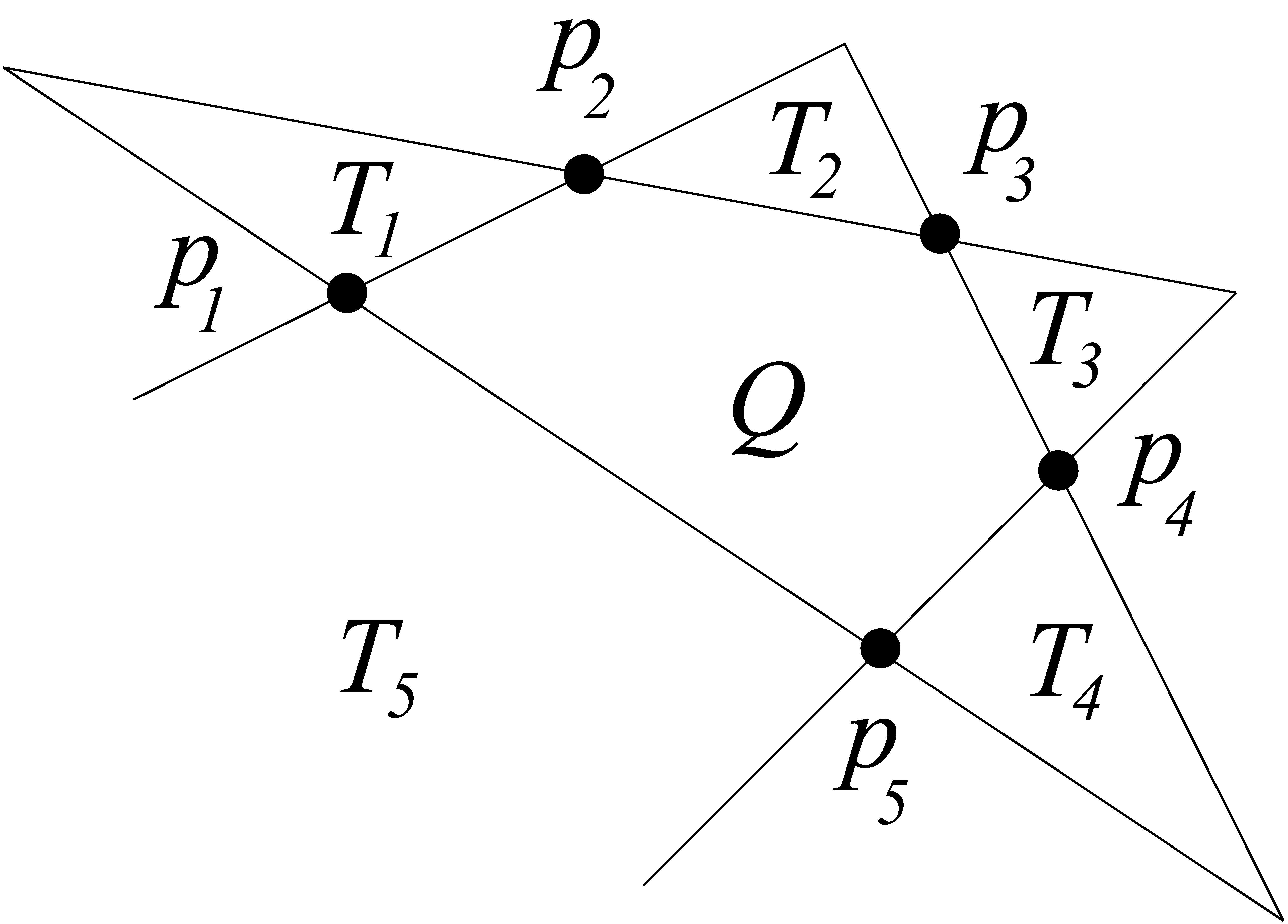
pontjait, amire ![]() is konvex helyzetű. Ezek a pontok
is konvex helyzetű. Ezek a pontok ![]() „tüskét” alkotnak, ahol az
„tüskét” alkotnak, ahol az ![]() -edik tüske (jelöljük ezt
-edik tüske (jelöljük ezt ![]() -vel) azon pontokbol áll, amelyeket az
-vel) azon pontokbol áll, amelyeket az ![]() egyenes elválaszt
egyenes elválaszt ![]() belsejétől, de sem a
belsejétől, de sem a ![]() sem a
sem a ![]() egyenes nem választ el
egyenes nem választ el ![]() belsejétől (4. ábra). Itt az indexeket modulo
belsejétől (4. ábra). Itt az indexeket modulo ![]() értjük. Ha
értjük. Ha ![]() , akkor a tüskék közül legfeljebb kettő lehet végtelen tartomány, a többi tüske háromszög lesz. Vegyük észre, hogy akárhogy is veszünk ki egy-egy pontot mindegyik tüskéből, a kapott ponthalmaz konvex helyzetű lesz. A következő lemma tehát nagyon sok konvex
, akkor a tüskék közül legfeljebb kettő lehet végtelen tartomány, a többi tüske háromszög lesz. Vegyük észre, hogy akárhogy is veszünk ki egy-egy pontot mindegyik tüskéből, a kapott ponthalmaz konvex helyzetű lesz. A következő lemma tehát nagyon sok konvex ![]() -szöget talál egy általános helyzetű ponthalmazban, ráadásul ezek jól struktúráltan helyezkednek el. Ez Pór Attila és Pavel Valtr [11] eredménye kicsit átfogalmazva.
-szöget talál egy általános helyzetű ponthalmazban, ráadásul ezek jól struktúráltan helyezkednek el. Ez Pór Attila és Pavel Valtr [11] eredménye kicsit átfogalmazva.
4. Lemma [11] Legyen ![]() általános helyzetű ponthalmaz a síkon. Ha
általános helyzetű ponthalmaz a síkon. Ha ![]() , akkor található egy
, akkor található egy ![]() elemű
elemű ![]() ponthalmaz konvex helyzetben, hogy az általa meghatározott
ponthalmaz konvex helyzetben, hogy az általa meghatározott ![]() tüskékre
tüskékre
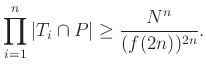
Bizonyítás. Egy egyszerű kettős leszámolással belátjuk, hogy sok konvex ![]() -szög van
-szög van ![]() -ben. Minden
-ben. Minden ![]() elemű részében
elemű részében ![]() -nek találunk legalább egy konvex
-nek találunk legalább egy konvex ![]() -szöget. Ez tehát
-szöget. Ez tehát ![]() konvex
konvex ![]() -szög, de ezek nem mind különbözőek. Egy fix
-szög, de ezek nem mind különbözőek. Egy fix ![]() elemű konvex helyzetű halmaz
elemű konvex helyzetű halmaz ![]() pontosan
pontosan ![]() darab
darab ![]() elemű részhalmazában szerepel, tehát legalább
elemű részhalmazában szerepel, tehát legalább
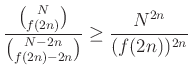
különböző konvex ![]() -szöget találtunk
-szöget találtunk ![]() -ben.
-ben.
Most hagyjuk el ezen konvex ![]() -szögek minden második csúcsát. Így egy konvex
-szögek minden második csúcsát. Így egy konvex ![]() -szöget kapunk. Nagyon durva felső becslést alkalmazva látjuk, hogy ilyen konvex
-szöget kapunk. Nagyon durva felső becslést alkalmazva látjuk, hogy ilyen konvex ![]() -szög maximum
-szög maximum ![]() van, így legalább
van, így legalább ![]() különböző konvex
különböző konvex ![]() -szögből ugyanazt az
-szögből ugyanazt az ![]() konvex
konvex ![]() -szöget kell kapnunk. Márpedig ha egy konvex
-szöget kell kapnunk. Márpedig ha egy konvex ![]() -szög minden második csúcsát elhagyva pont
-szög minden második csúcsát elhagyva pont ![]() -et kapjuk, akkor az
-et kapjuk, akkor az ![]() -hez tartozó
-hez tartozó ![]() tüskék mindegyikéből pontosan egy pontot hagytunk el, így a szóba jöhető konvex
tüskék mindegyikéből pontosan egy pontot hagytunk el, így a szóba jöhető konvex ![]() -szögek száma maximum
-szögek száma maximum ![]() . Ez pont a lemma állítását igazolja.
. Ez pont a lemma állítását igazolja. ![]()
Áttekintés
Andrew Suk bizonyítása így foglalható össze. Megfelelően nagy általános helyzetű ponthalmazban próbál konvex ![]() -szöget találni. Ehhez a 4. Lemmát használja
-szöget találni. Ehhez a 4. Lemmát használja ![]() helyett egy sokkal kisebb
helyett egy sokkal kisebb ![]() értékre, és az így talált
értékre, és az így talált ![]() konvex
konvex ![]() -szög
-szög ![]() tüskéiben használja külön-külön Erdős és Szekeres hegyekre és völgyekre vonatkozó éles eredményét. Nem kétféle (hegy és völgy) részhalmazt keres
tüskéiben használja külön-külön Erdős és Szekeres hegyekre és völgyekre vonatkozó éles eredményét. Nem kétféle (hegy és völgy) részhalmazt keres ![]() -ben, hanem négyféle „irányultságot” különböztet meg: (1) a
-ben, hanem négyféle „irányultságot” különböztet meg: (1) a ![]() -felől nézve domború (az
-felől nézve domború (az ![]() sokszögre „ráboruló”) íveket; (2) a
sokszögre „ráboruló”) íveket; (2) a ![]() felől nézve homorú (
felől nézve homorú (![]() -tól „elhajló”) íveket; (3) a balról,
-tól „elhajló”) íveket; (3) a balról, ![]() felől nézve domború íveket; és végül (4) a jobbról,
felől nézve domború íveket; és végül (4) a jobbról, ![]() -felől nézve domború íveket. A pontos definiciót lásd később. A gondolatmenet lényege, hogy (1)-es típusú íveket minden második tüskéből egyesíteni lehet, és még így is konvex helyzetű ponthalmazokat kapunk (5. ábra), valamint egy
-felől nézve domború íveket. A pontos definiciót lásd később. A gondolatmenet lényege, hogy (1)-es típusú íveket minden második tüskéből egyesíteni lehet, és még így is konvex helyzetű ponthalmazokat kapunk (5. ábra), valamint egy ![]() tüskében lévő „jobbról domború”, azaz (4)-es típusú ív és a következő
tüskében lévő „jobbról domború”, azaz (4)-es típusú ív és a következő ![]() tüskében lévő „balról domború”, azaz (3)-as típusú ív úniója is konvex helyzetű (6. ábra).
tüskében lévő „balról domború”, azaz (3)-as típusú ív úniója is konvex helyzetű (6. ábra).
Ha ![]() megfelelően kicsi
megfelelően kicsi ![]() -hez képest, akkor a 4. Lemma nagyon hatékony. Legyen
-hez képest, akkor a 4. Lemma nagyon hatékony. Legyen ![]() a lemma által biztosított
a lemma által biztosított ![]() -szög. A
-szög. A ![]() -hoz tartozó egyetlen átlagos
-hoz tartozó egyetlen átlagos ![]() tüskében a ponthalmazunk
tüskében a ponthalmazunk ![]() pontjából legalább
pontjából legalább ![]() darab esik, szóval alig vesztünk valamit. A következő lépés a
darab esik, szóval alig vesztünk valamit. A következő lépés a ![]() -be eső pontpárok közötti szakaszok osztályozása „laposra” , azaz a
-be eső pontpárok közötti szakaszok osztályozása „laposra” , azaz a ![]()
![]() -szög
-szög ![]() -t határoló oldalával majdnem párhuzamosra és „meredekre”. Egy klasszikus kombinatorikai tétel, a Dilworth-tétel biztosítja, hogy találunk egy nagy halmazt a
-t határoló oldalával majdnem párhuzamosra és „meredekre”. Egy klasszikus kombinatorikai tétel, a Dilworth-tétel biztosítja, hogy találunk egy nagy halmazt a ![]() -ben, hogy a köztük levő szakaszok mind laposak, vagy mind meredekek. A lapos esetben a klasszikus hegy-völgy tétel alapján találunk nagy (1)-es vagy (2)-es típusú ívet, a meredek esetben ugyanez a tétel biztosítja, hogy nagy (3)-as vagy (4)-es típusú ívet találunk. Itt az (1)-es típusú ívekből olyan sokat tudunk összefűzni, hogy ha így sem kapunk konvex
-ben, hogy a köztük levő szakaszok mind laposak, vagy mind meredekek. A lapos esetben a klasszikus hegy-völgy tétel alapján találunk nagy (1)-es vagy (2)-es típusú ívet, a meredek esetben ugyanez a tétel biztosítja, hogy nagy (3)-as vagy (4)-es típusú ívet találunk. Itt az (1)-es típusú ívekből olyan sokat tudunk összefűzni, hogy ha így sem kapunk konvex ![]() -szöget, akkor a lapos részek nagyon kicsik kell, hogy legyenek. A meredek részeknél meg épp két ívet tudunk összefűzni, ez adja a körülbelül kettes faktor javulást (konvex
-szöget, akkor a lapos részek nagyon kicsik kell, hogy legyenek. A meredek részeknél meg épp két ívet tudunk összefűzni, ez adja a körülbelül kettes faktor javulást (konvex ![]() -szög helyett konvex
-szög helyett konvex ![]() -szög), ami Suk bizonyításának a lényege.
-szög), ami Suk bizonyításának a lényege.
A fenti intuíciót a következőkben precízebbé tesszük. A részletekben Suk eredeti bizonyítása, [14], helyett a Holmsen-Mojarrad-Pach-Tardos bizonyítást követjük, [5].
Részletek
Rögzítsünk egy nagy ![]() természetes számot és egy általános helyzetű
természetes számot és egy általános helyzetű ![]() ponthalmazt a síkban, ami nem tartalmaz
ponthalmazt a síkban, ami nem tartalmaz ![]() pontot konvex helyzetben. Célunk egy felső korlátot adni
pontot konvex helyzetben. Célunk egy felső korlátot adni ![]() függvényében az
függvényében az ![]() számosságra. Ez a korlát (pontosabban az eggyel nagyobb szám) nyilván
számosságra. Ez a korlát (pontosabban az eggyel nagyobb szám) nyilván ![]() -nek is korlátja.
-nek is korlátja.
Először is választunk egy páros ![]() számot, mely jóval kisebb
számot, mely jóval kisebb ![]() -nél. Alkalmazzuk a 4. Lemmát erre a
-nél. Alkalmazzuk a 4. Lemmát erre a ![]() számra. Ha
számra. Ha ![]() , akkor kapunk egy
, akkor kapunk egy ![]() konvex
konvex ![]() -szöget úgy hogy a hozzátartozó
-szöget úgy hogy a hozzátartozó ![]() tüskék teljesítik, hogy
tüskék teljesítik, hogy
ahol ![]() .
.
Tegyük fel az egyszerűség kedvéért, hogy a ![]() tüskék mind háromszögek. Ez a feltevés két különböző okból sem jelent valódi megszorítást. Egyfelől pontosan ugyanezt a becslést lehet nagyon hasonlóan bizonyítani a feltételezés nélkül is, csak ehhez a végtelen tüskékben keresett ponthalmazokat kicsit körülményesebben kellene definiálnunk. Másfelől pedig használhatjuk, hogy
tüskék mind háromszögek. Ez a feltevés két különböző okból sem jelent valódi megszorítást. Egyfelől pontosan ugyanezt a becslést lehet nagyon hasonlóan bizonyítani a feltételezés nélkül is, csak ehhez a végtelen tüskékben keresett ponthalmazokat kicsit körülményesebben kellene definiálnunk. Másfelől pedig használhatjuk, hogy ![]() esetén legfeljebb kettő tüske nem háromszög. Ha ezekben a végtelen tüskékben egyáltalán nem keresünk konvex helyzetű ponthalmazokat, és csak a véges tüskékre koncentrálunk, akkor a hasonló módszerrel kapott becslés csak egy konstans faktorral lesz rosszabb, azaz a kitevőben szereplő hibatag csak egy additív konstanssal nő.
esetén legfeljebb kettő tüske nem háromszög. Ha ezekben a végtelen tüskékben egyáltalán nem keresünk konvex helyzetű ponthalmazokat, és csak a véges tüskékre koncentrálunk, akkor a hasonló módszerrel kapott becslés csak egy konstans faktorral lesz rosszabb, azaz a kitevőben szereplő hibatag csak egy additív konstanssal nő.
Most egy fix ![]() halmazt vizsgálunk és definiálunk rajta egy részbenrendezést. Az
halmazt vizsgálunk és definiálunk rajta egy részbenrendezést. Az ![]() pontokra azt mondjuk, hogy
pontokra azt mondjuk, hogy ![]() , ha a
, ha a ![]() háromszög tartalmazza a
háromszög tartalmazza a ![]() háromszöget. Itt és a továbbiakban az indexeket modulo
háromszöget. Itt és a továbbiakban az indexeket modulo ![]() értjük. Ez nyilván részbenrendezés. A bizonyítás áttekintésében az összehasonlítható pontpárok közötti szakaszt mondtuk meredeknek, a nem összehasonlíthatóak közöttit meg laposnak. Láncnak mondjuk
értjük. Ez nyilván részbenrendezés. A bizonyítás áttekintésében az összehasonlítható pontpárok közötti szakaszt mondtuk meredeknek, a nem összehasonlíthatóak közöttit meg laposnak. Láncnak mondjuk ![]() egy részhalmazát, ha bármely két eleme összehasonlítható ebben a részbenrendezésben, antiláncnak meg az olyan részhalmazt mondjuk, amely nem tartalmaz összehasonlítható elemeket. Dilworth tétele (illetve annak egyszerűbb iránya) szerint van olyan
egy részhalmazát, ha bármely két eleme összehasonlítható ebben a részbenrendezésben, antiláncnak meg az olyan részhalmazt mondjuk, amely nem tartalmaz összehasonlítható elemeket. Dilworth tétele (illetve annak egyszerűbb iránya) szerint van olyan ![]() lánc és
lánc és ![]() antilánc
antilánc ![]() -ben, amelyekre
-ben, amelyekre
Válasszuk meg a koordináta-rendszert úgy, hogy a ![]() egyenes az
egyenes az ![]() -tengellyel párhuzamos (függőleges) legyen, és
-tengellyel párhuzamos (függőleges) legyen, és ![]()
![]() fölött helyezkedjen el. Ezzel meghatároztuk, hogy
fölött helyezkedjen el. Ezzel meghatároztuk, hogy ![]() részhalmazai közül melyek a hegyek és melyek a völgyek. Legyen
részhalmazai közül melyek a hegyek és melyek a völgyek. Legyen ![]() és
és ![]() a legnagyobb hegy, illetve völgy az
a legnagyobb hegy, illetve völgy az ![]() antiláncon belül. A bizonyítás áttekintésében ezeket hívtuk (1)-es és (2)-es típusú íveknek. Az
antiláncon belül. A bizonyítás áttekintésében ezeket hívtuk (1)-es és (2)-es típusú íveknek. Az ![]() halmazban nincs sem
halmazban nincs sem ![]() -hegy sem
-hegy sem ![]() -völgy, így az 1. Tétel szerint
-völgy, így az 1. Tétel szerint
Meg kell még említeni, hogy az 1. Tétel csak olyan ponthalmazokra alkalmazható, ahol az ![]() -koordináták mind különböznek, de mivel feltettük, hogy a
-koordináták mind különböznek, de mivel feltettük, hogy a ![]() tüske egy háromszög,
tüske egy háromszög, ![]() pedig egy antilánc, ez teljesül.
pedig egy antilánc, ez teljesül.
Most forgassuk el a koordináta-rendszert, mégpedig úgy, hogy ![]() épp függőlegesen
épp függőlegesen ![]() fölött legyen. Legyen
fölött legyen. Legyen ![]() , illetve
, illetve ![]() a legnagyobb hegy, illetve völgy a
a legnagyobb hegy, illetve völgy a ![]() láncban erre a koordináta-rendszerre nézve. A bizonyítás áttekintésében ezeket hívtuk (3)-as, illetve (4)-es típusú íveknek. Mivel
láncban erre a koordináta-rendszerre nézve. A bizonyítás áttekintésében ezeket hívtuk (3)-as, illetve (4)-es típusú íveknek. Mivel ![]() lánc, pontjainak
lánc, pontjainak ![]() -koordinátái különbözőek, így alkalmazhatjuk az 1. Tételt:
-koordinátái különbözőek, így alkalmazhatjuk az 1. Tételt:
Egyszerű geometriai megfontolás mutatja, hogy ![]() konvex helyzetben van (5. ábra), és ugyanez vonatkozik
konvex helyzetben van (5. ábra), és ugyanez vonatkozik ![]() -ra is. (Itt is használjuk a feltevést, hogy minden tüske véges.) Feltettük, hogy a
-ra is. (Itt is használjuk a feltevést, hogy minden tüske véges.) Feltettük, hogy a ![]() ponthalmazban nincs
ponthalmazban nincs ![]() pont konvex helyzetben, így
pont konvex helyzetben, így
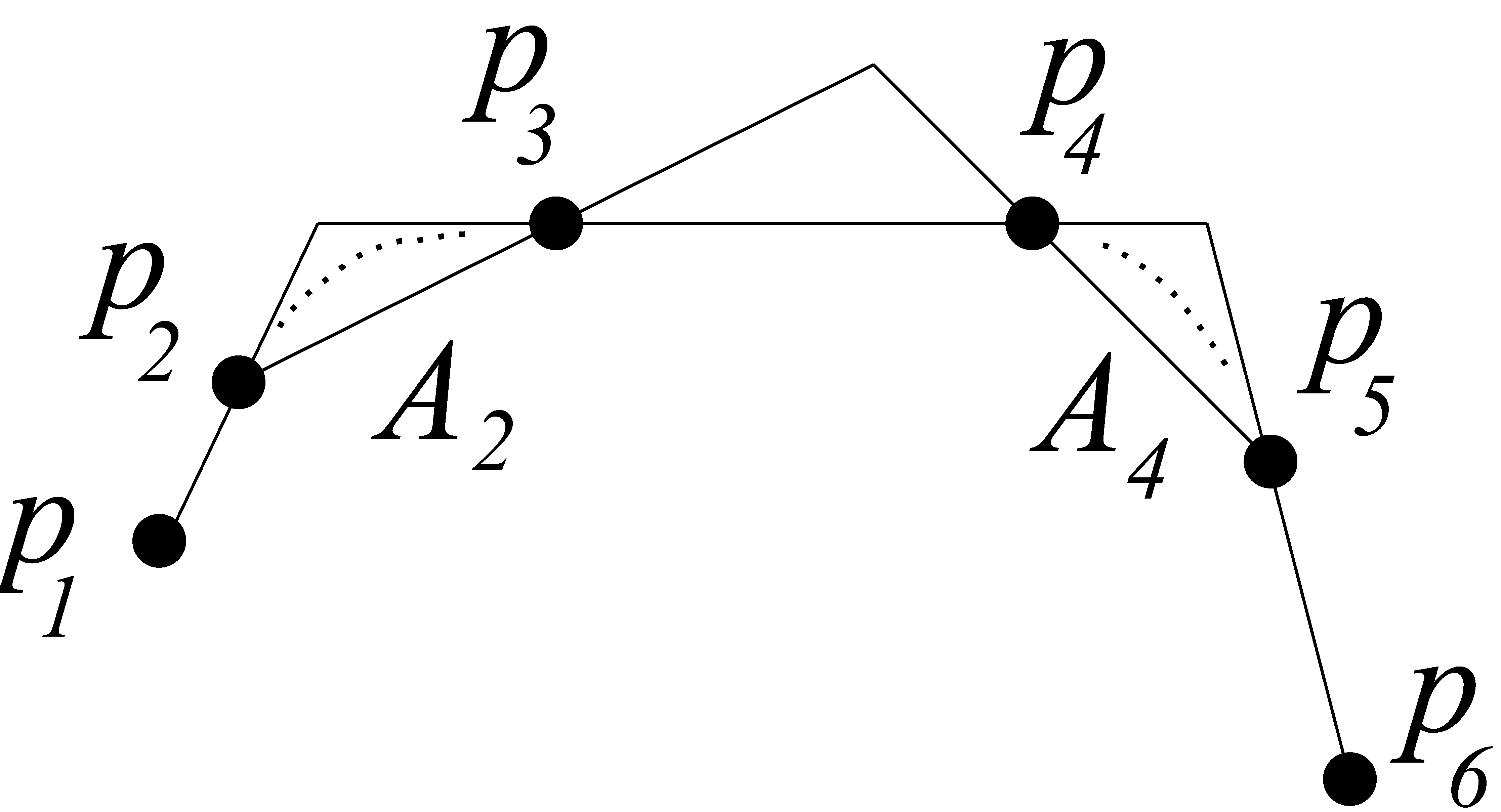
5. ábra. ![]() konvex helyzetben van.
konvex helyzetben van.
A ![]() halmazokat nem tudjuk kombinálni, de egyenként mindegyik konvex helyzetben van, tehát
halmazokat nem tudjuk kombinálni, de egyenként mindegyik konvex helyzetben van, tehát
teljesül minden ![]() -re.
-re.
Nem nehéz azt sem belátni, hogy a ![]() halmaz is konvex helyzetben van minden
halmaz is konvex helyzetben van minden ![]() esetén (6. ábra), így
esetén (6. ábra), így ![]() , tehát
, tehát
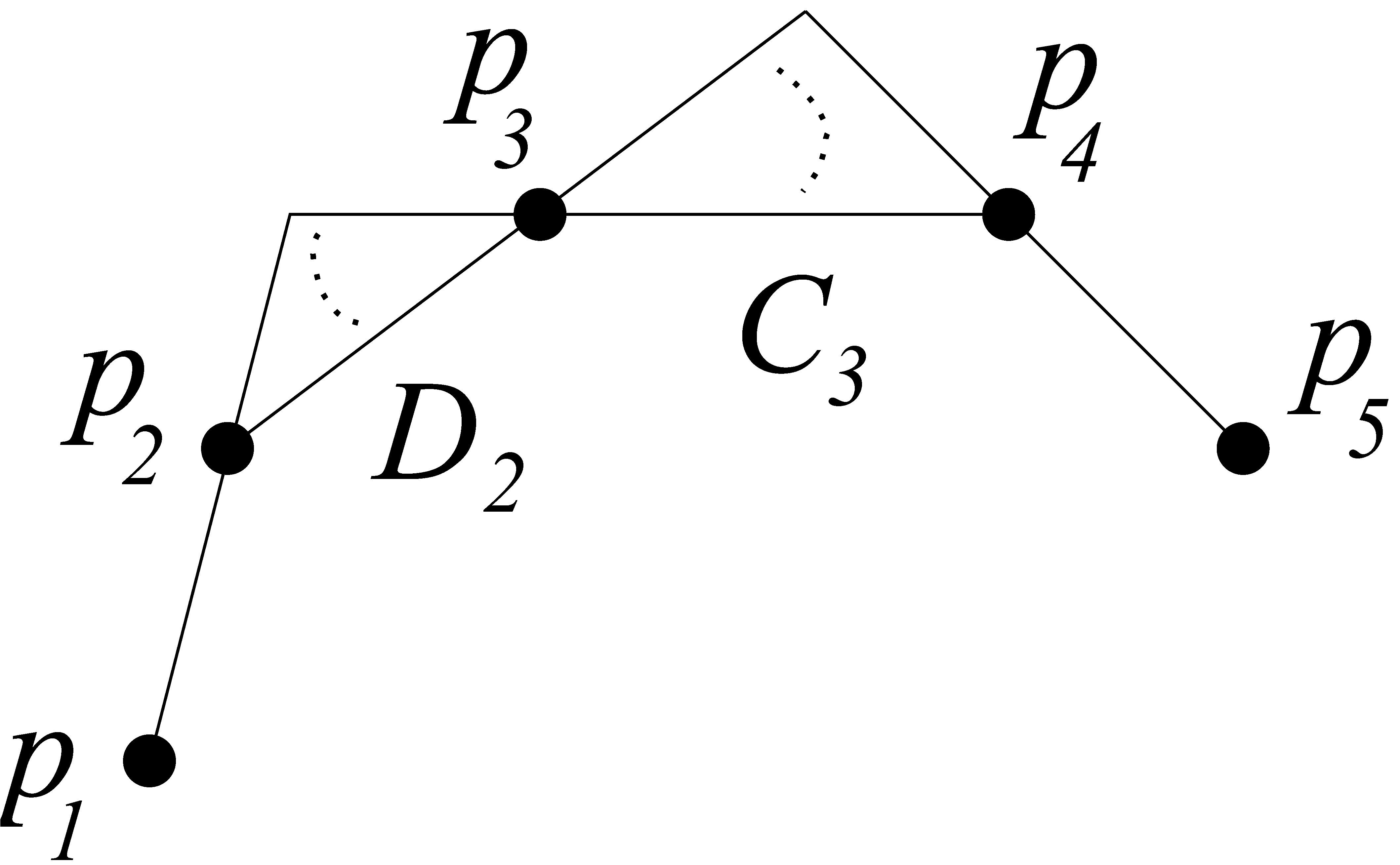
6. ábra. ![]() konvex helyzetben van.
konvex helyzetben van.
A bizonyítás befejezéséhez már csak némi számolásra van szükség. Először a (3) és (6) egyenlőtlenségekből, valamint egy elemi binomiális együtthatókra vonatkozó becslésből kapjuk az alábbiakat:
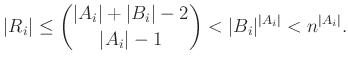
Szorozzuk össze ezt a becslést minden ![]() -re és alkalmazzuk az (5) egyenlőtlenséget:
-re és alkalmazzuk az (5) egyenlőtlenséget:
A (4) egyenlőtlenségnél a binomiális együtthatót durván becsülve kapjuk, hogy ![]() és így a (7) egyenlőtlenséget is használva adódik, hogy
és így a (7) egyenlőtlenséget is használva adódik, hogy
Végül az (1), (2), (8) és (9) egyenlőtlenségekből kapjuk, hogy
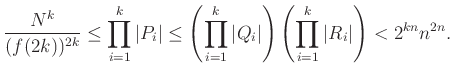
Itt elég a durva ![]() becslést alkalmaznunk, és átrendezéssel kapjuk, hogy
becslést alkalmaznunk, és átrendezéssel kapjuk, hogy
Látszik, hogy ![]() legjobb választása
legjobb választása ![]() körül van, ahonnan
körül van, ahonnan
lesz a végső korlátunk. A ![]() azért került a kitevőbe, mert
azért került a kitevőbe, mert ![]() értéke nem mindig lehet pont
értéke nem mindig lehet pont ![]() , hiszen páros egész számot kell választanunk.
, hiszen páros egész számot kell választanunk.
Itt ![]() sejtett értéke (és egyben az alsó korlátja)
sejtett értéke (és egyben az alsó korlátja) ![]() , így a fenti becslés kitevőjében
, így a fenti becslés kitevőjében ![]() tekinthető a hibatagnak. Ebben a 8-as faktor 6 alá csökkenthető azzal, ha
tekinthető a hibatagnak. Ebben a 8-as faktor 6 alá csökkenthető azzal, ha ![]() értékének becslésére a bizonyításban nem Erdős és Szekeres eredeti felső korlátját használtuk, hanem az épp bizonyított jobb becslést alkalmazzuk indukcióval.
értékének becslésére a bizonyításban nem Erdős és Szekeres eredeti felső korlátját használtuk, hanem az épp bizonyított jobb becslést alkalmazzuk indukcióval.
Irodalomjegyzék
[1] F. R. K. Chung and R. L. Graham, Forced convex ![]() -gons in the plane, Discrete and Computational Geometry 19 (1998), 367—371.
-gons in the plane, Discrete and Computational Geometry 19 (1998), 367—371.
[2] P. Erdős, G. Szekeres, A combinatorial problem in geometry, Compositio Mathematica 2 (1935), 463—470.
[3] P. Erdős, G. Szekeres, On some extremum problems in elementary geometry, Ann. Univ. Sci. Eötvös Sect. Math 3-4 (1961), 53—62.
[4] K. Hartnett, A Puzzle of Clever Connections Nears a Happy End, Quanta Magazine (2017).
[5] A. Holmsen, H. Mojarrad, J. Pach, G. Tardos, Two extensions of the Erdős—Szekeres problem, arXiv:1710.11415, (2017).
[6] D. J. Kleitman and L. Pachter, Finding convex sets among points in the plane, Discrete and Computational Geometry 19 (1998), 405—410.
[7] H. Mojarrad, G. Vlachos, An Improved Upper Bound for the Erdős—Szekeres Conjecture, Discrete and Computational Geometry 56 (2016), 165—180.
[8] W. Morris, V. Soltan, The Erdős—Szekeres problem on points in convex position—a survey, Bulletin of the American Mathematical Society 37, (2000), 437—458.
[9] S. Norin, Y. Yuditsky, Erdős—Szekeres without induction, Discrete and Computational Geometry 55 (2016), 963—971.
[10] Pach J., A Happy End probléma — A kombinatorikus geometria kezdetei, Új matematikai mozaik (Hraskó A., szerk.) Typotex, Budapest, 2002, 223-242.
[11] A. Pór and P. Valtr, The partitioned version of the Erdős—Szekeres theorem, Discrete and Computational Geometry 28 (2002), 625—637.
[12] G. Szekeres, L. Peters, Computer solution to the 17-point Erdős—Szekeres problem, The ANZIAM Journal 48 (2006), 151—164.
[13] F. P. Ramsey: On a problem of formal logic, Proceedings of the London Mathematical Society 30 (1930), 338—384.
[14] A. Suk, On the Erdős—Szekeres convex polygon problem, Journal of the American Mathematical Society 30 (2017), 1047—1053.
[15] G. Vlachos, On a conjecture of Erdős and Szekeres, arXiv:1505.07549, (2015).
[16] G. Tóth and P. Valtr, Note on the Erdős—Szekeres theorem, Discrete and Computational Geometry 19 (1998), 457—459.
[17] G. Tóth and P. Valtr, The Erdős—Szekeres theorem, upper bounds and generalizations, Discrete and Computational Geometry — Papers from the MSRI Special Program (J. E. Goodman et al. eds.), MSRI Publications 52 Cambridge University Press, Cambridge (2005), 557—568.
Tardos Gábor és Tóth Géza
MTA Rényi Alfréd Matematikai Kutatóintézet
Tardos Gábor kutatásait az MTA Kriptográfia „Lendület” programja valamint a Nemzeti Kutatási és Innovációs Hivatal K-116769-es és SSN-117879-es számú programjai támogatják, Tóth Géza kutatásait a Nemzeti Kutatási és Innovációs Hivatal K-111827-es számú programja támogatja.
Andrew Suk bemutatása: https://math.ucsd.edu/people/