Képzeljük el a következő szituációt. A háromdimenziós térben van egy tárgy, ![]() , amelynek pontos helyzetét szeretnénk megtudni. Ehhez van négy állomásunk,
, amelynek pontos helyzetét szeretnénk megtudni. Ehhez van négy állomásunk, ![]() és
és ![]() , amelyeknek az
, amelyeknek az ![]() -től vett euklideszi távolságait tudjuk mérni. E négy mennyiség alapján meg tudjuk-e állapítani
-től vett euklideszi távolságait tudjuk mérni. E négy mennyiség alapján meg tudjuk-e állapítani ![]() helyzetét?
helyzetét?
Az egyszerűség kedvéért feltesszük, hogy ![]() és
és ![]() helyzete fix, tehát az állomások és a tárgy nem mozognak. Tekintsük előbb a problémát egy egyszerűbb szituációban, a síkon. Ekkor három állomás adott:
helyzete fix, tehát az állomások és a tárgy nem mozognak. Tekintsük előbb a problémát egy egyszerűbb szituációban, a síkon. Ekkor három állomás adott: ![]() és
és ![]() , amelyek euklideszi távolságait
, amelyek euklideszi távolságait ![]() -től, azaz
-től, azaz ![]() -t,
-t, ![]() -t és
-t és ![]() -t megmértük, és ez alapján szeretnénk kiszámolni, hogy
-t megmértük, és ez alapján szeretnénk kiszámolni, hogy ![]() hol helyezkedik el. Kérdés, hogy elegendő információ áll-e ehhez a rendelkezésünkre? Vegyük észre, hogy abban a speciális esetben, amikor a három állomás egy egyenesen fekszik, nincs elég információnk, ugyanis ha tükrözzük
hol helyezkedik el. Kérdés, hogy elegendő információ áll-e ehhez a rendelkezésünkre? Vegyük észre, hogy abban a speciális esetben, amikor a három állomás egy egyenesen fekszik, nincs elég információnk, ugyanis ha tükrözzük ![]() -t az állomások által kifeszített egyenesre, akkor a kapott
-t az állomások által kifeszített egyenesre, akkor a kapott ![]() pont távolsága nyilván ugyanaz lesz az állomásoktól, mint
pont távolsága nyilván ugyanaz lesz az állomásoktól, mint ![]() -é (lásd az 1. ábrát). Ha viszont feltesszük, hogy a három állomás nem esik egy egyenesre, azaz egy valódi háromszöget feszítenek ki a síkon, akkor már elegendő információnk van ahhoz, hogy
-é (lásd az 1. ábrát). Ha viszont feltesszük, hogy a három állomás nem esik egy egyenesre, azaz egy valódi háromszöget feszítenek ki a síkon, akkor már elegendő információnk van ahhoz, hogy ![]() pozícióját meghatározzuk. Ennek bizonyításához két lehetséges gondolatmenet vázolunk, amelyek közül talán az első amire azonnal gondolna az ember, a második pedig egy „fordított gondolatmenet”, amelyről azonban később kiderül, hogy hasznosabb.
pozícióját meghatározzuk. Ennek bizonyításához két lehetséges gondolatmenet vázolunk, amelyek közül talán az első amire azonnal gondolna az ember, a második pedig egy „fordított gondolatmenet”, amelyről azonban később kiderül, hogy hasznosabb.
1. Vegyük észre, hogy ![]() három körvonal metszetén kell, hogy feküdjön, amelyeknek ez esetben nem lehet egynél több metszéspontja.
három körvonal metszetén kell, hogy feküdjön, amelyeknek ez esetben nem lehet egynél több metszéspontja.
2. Tegyük fel, hogy nem igaz az állítás, és van még egy ![]() pont , amitől mért távolságok egyeznek az
pont , amitől mért távolságok egyeznek az ![]() -től mért távolságokkal. Ez azt jelenti, hogy
-től mért távolságokkal. Ez azt jelenti, hogy ![]() távolsága
távolsága ![]() -től és
-től és ![]() -től megegyezik minden
-től megegyezik minden ![]() esetén, azaz
esetén, azaz ![]() az
az ![]() és
és![]() felező merőlegesén kell hogy legyen, ami ellentmond feltevésünknek, hiszen ez egy egyenes (lásd megint az 1. ábrát).
felező merőlegesén kell hogy legyen, ami ellentmond feltevésünknek, hiszen ez egy egyenes (lásd megint az 1. ábrát).
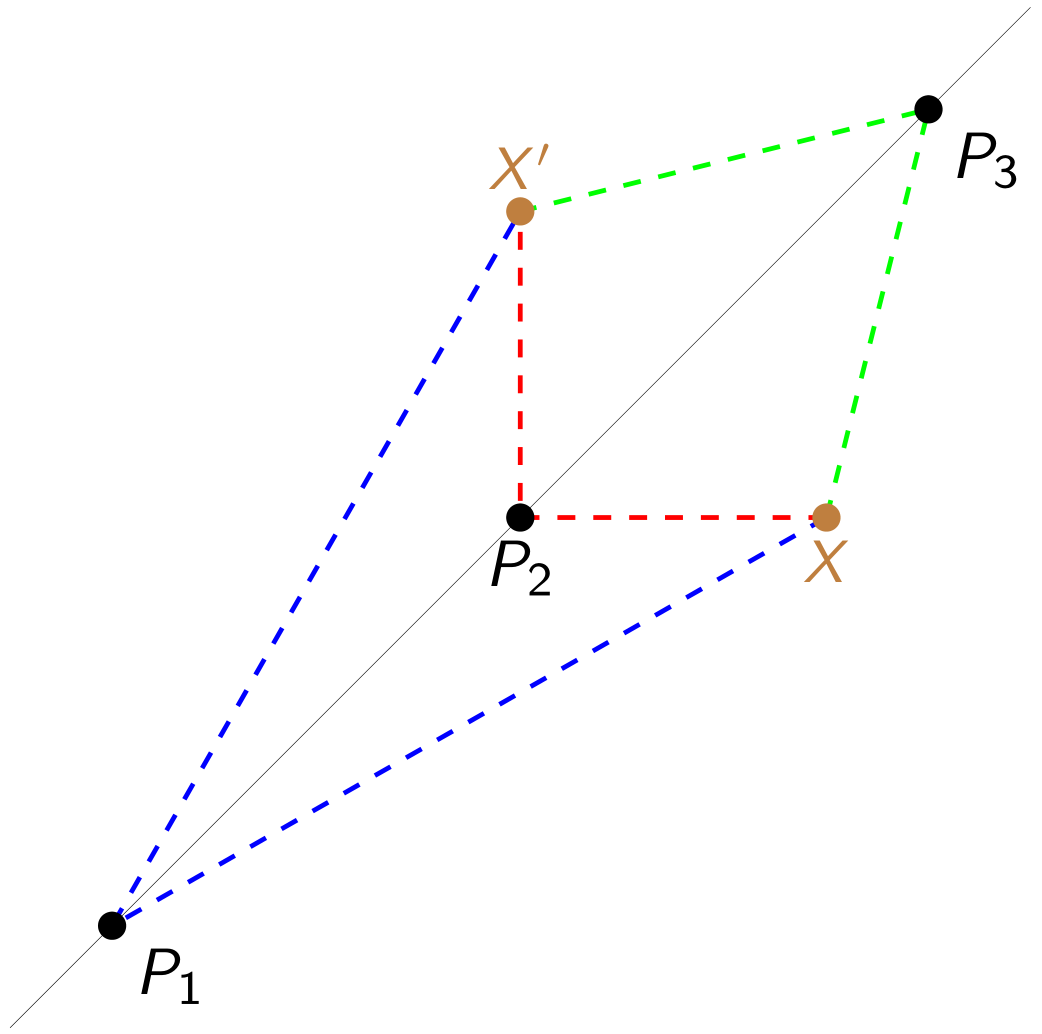
1. ábra. A színes szaggatott vonalak azt jelzik, hogy az adott távolságok megegyeznek. A ![]() ,
, ![]() ,
, ![]() pontokon átmenő egyenes az
pontokon átmenő egyenes az ![]() és
és ![]() pontok felező merőleges egyenese.
pontok felező merőleges egyenese.
Most tekintsük a háromdimenziós esetet. Természetesen, ha az állomások egy síkra esnek, akkor megint csak ha tükrözzük ![]() -et erre a síkra, akkor a kapott
-et erre a síkra, akkor a kapott ![]() pont távolsága
pont távolsága ![]() -től ugyanaz mint
-től ugyanaz mint ![]() -é minden
-é minden ![]() -re. Ezért itt is feltesszük, hogy
-re. Ezért itt is feltesszük, hogy ![]() és
és ![]() nem esik egy síkra. Ez esetben is alkalmazható a fenti első gondolatmenet, de sokkal jobban átlátható a második „ fordított gondolatmenet”. Tehát tegyük fel, hogy nem igaz az állítás, és van még egy
nem esik egy síkra. Ez esetben is alkalmazható a fenti első gondolatmenet, de sokkal jobban átlátható a második „ fordított gondolatmenet”. Tehát tegyük fel, hogy nem igaz az állítás, és van még egy ![]() pont, amitől mért távolságok egyeznek az
pont, amitől mért távolságok egyeznek az ![]() -től mért távolságokkal. Ekkor minden
-től mért távolságokkal. Ekkor minden ![]() az
az ![]() és
és ![]() felező merőleges síkján található, ami ellentmond feltevésünknek.
felező merőleges síkján található, ami ellentmond feltevésünknek.
A fenti elvet (elhanyagolva az Einstein-féle relativitáselméletet és azt, hogy a méréseink sosem teljesen pontosak) alkalmazza a GPS (Global Positioning System) is, általában 4-5 műhold segítségével tudja műszerünk kiszámolni nagyon pontosan, hogy hol vagyunk.
A matematika különféle ágaiban (elméleti és alkalmazott területeken egyaránt) felmerülnek olyan problémák, amikor szükség van arra, hogy a távolságot nem a fenti euklideszi értelemben mérjük, hanem egy jóval általánosabb, úgynevezett norma segítségével.
Egy ![]() függvényt normának hívunk, ha teljesíti az alábbi három feltételt:
függvényt normának hívunk, ha teljesíti az alábbi három feltételt:
- (pozitív definitség)
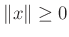 minden
minden 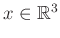 esetén, és
esetén, és 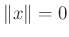 pontosan akkor ha
pontosan akkor ha 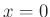 ,
, - (pozitív homogenitás)
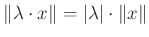 tetszőleges
tetszőleges 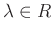 és
és 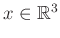 esetén,
esetén, - (háromszög-egyenlőtlenség)
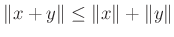 minden
minden 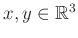 .
.
Azt mondjuk, hogy ![]() a
a ![]() normával felruházva egy háromdimenziós valós normált tér. Ez esetben az
normával felruházva egy háromdimenziós valós normált tér. Ez esetben az ![]() és
és ![]() pontok távolságát a
pontok távolságát a ![]() mennyiség definiálja. Teljesen hasonlóan definiáljuk a kétdimenziós valós normált tereket. Természetesen a szokásos euklideszi norma
mennyiség definiálja. Teljesen hasonlóan definiáljuk a kétdimenziós valós normált tereket. Természetesen a szokásos euklideszi norma
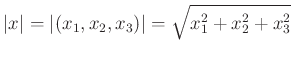
normát definiál ![]() -on a fenti értelemben.
-on a fenti értelemben.
Most adunk néhány további példát. Tegyük fel, hogy ![]() valós szám, ekkor az alábbi,
valós szám, ekkor az alábbi, ![]() -norma néven ismert mennyiség szintén normát definiál
-norma néven ismert mennyiség szintén normát definiál ![]() -on (hasonlóan
-on (hasonlóan ![]() -n):
-n):
A normatulajdonságok közül egyedül a háromszög-egyenlőtlenség nem triviális, amely Minkowski-egyenlőtlenség néven vonult be a történelembe . A figyelmes olvasó észreveheti, hogy a Minkowski-egyenlőtlenség az úgynevezett ![]() esetben is kimondható.
esetben is kimondható.
Egy vektor ![]() -normáján a következő mennyiséget értjük:
-normáján a következő mennyiséget értjük:
Ez ugyancsak normát definiál ![]() -on. Megjegyezzük, hogy a 2-norma az euklideszi normát adja vissza, illetve, hogy az eddig említett normákon kívül még rengeteg más normát lehet definiálni.
-on. Megjegyezzük, hogy a 2-norma az euklideszi normát adja vissza, illetve, hogy az eddig említett normákon kívül még rengeteg más normát lehet definiálni.
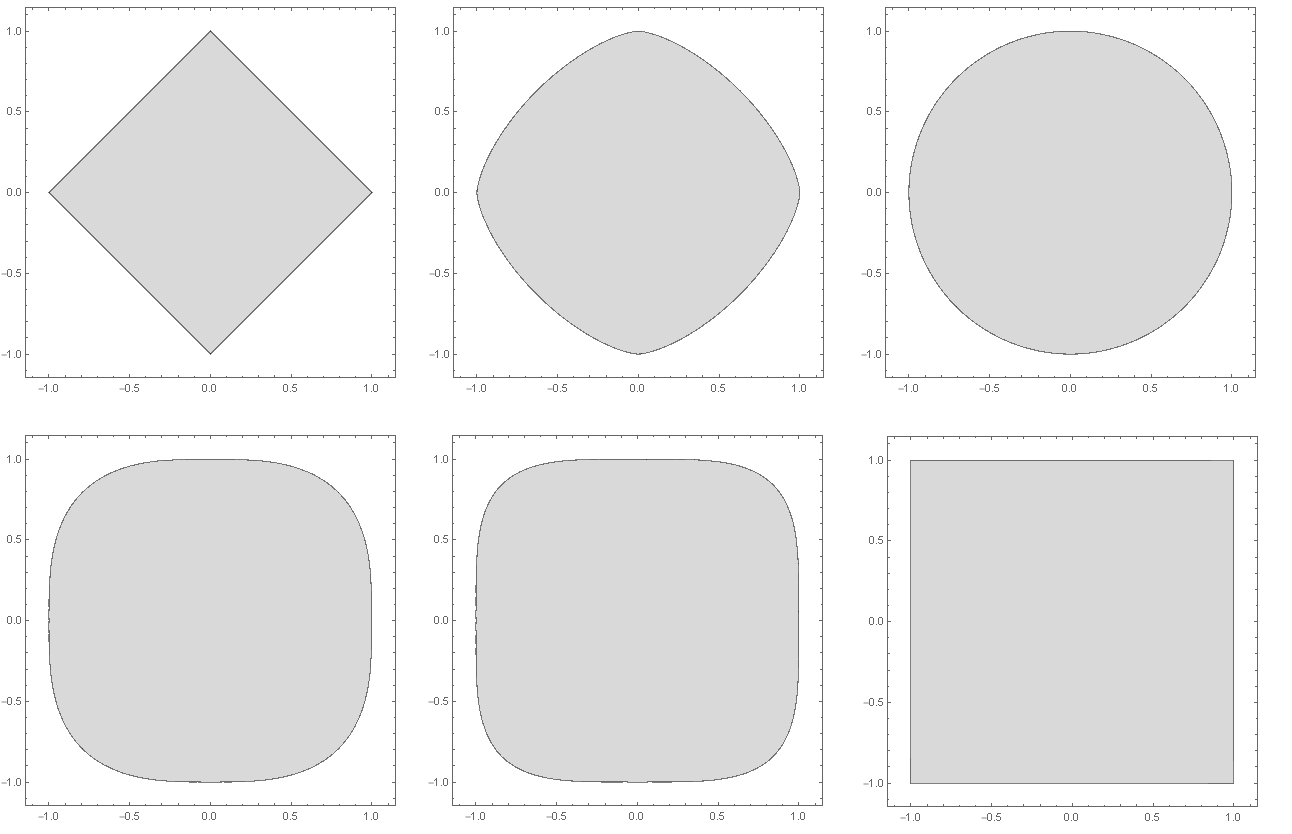
2. ábra. Néhány ![]() -norma egységkörlapja a síkon, balról jobbra haladva a
-norma egységkörlapja a síkon, balról jobbra haladva a ![]() ,
, ![]() , 2, 3, 4 és
, 2, 3, 4 és ![]() esetek láthatóak.
esetek láthatóak.
Egy norma szerinti egységgömbön (a sík esetén egységkörlapon) azon pontok halmazát értjük, amelyek legfeljebb 1 távolságra helyezkednek el az origótól. A 2. és a 3. ábra néhány ![]() -norma egységkörlapját és egységgömbjét illusztrálja a síkon, illetve a térben. Érdekességként megemlítjük, hogy az 1-norma esete Manhattan- vagy taxinorma néven is ismert, hiszen egy Manhattanben (melynek utcái négyzetrácsos mintát adnak) vezető taxisnak (megközelítően)
-norma egységkörlapját és egységgömbjét illusztrálja a síkon, illetve a térben. Érdekességként megemlítjük, hogy az 1-norma esete Manhattan- vagy taxinorma néven is ismert, hiszen egy Manhattanben (melynek utcái négyzetrácsos mintát adnak) vezető taxisnak (megközelítően) ![]() távolságot kell vezetnie az
távolságot kell vezetnie az ![]() ponttól
ponttól ![]() -ig.
-ig.
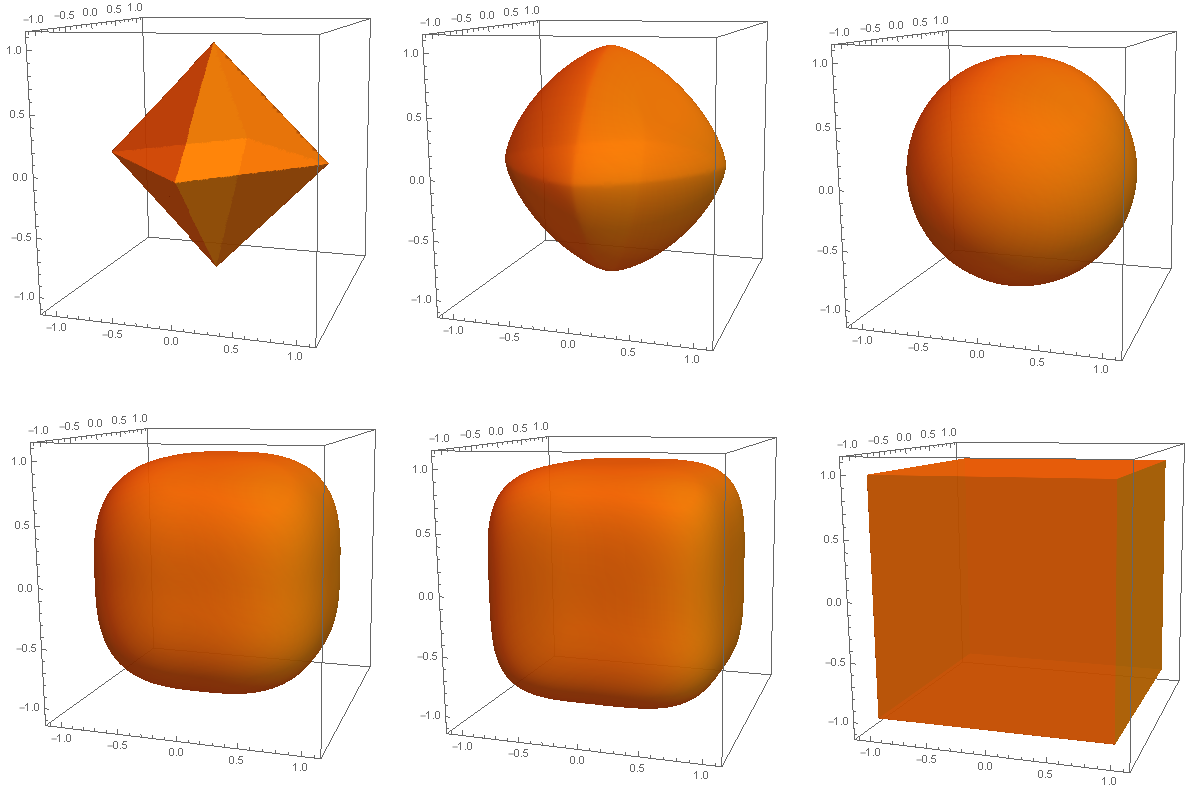
3. ábra. Néhány ![]() -norma egységgömbje a térben, balról jobbra haladva a
-norma egységgömbje a térben, balról jobbra haladva a ![]() ,
, ![]() , 2, 3, 4 és
, 2, 3, 4 és ![]() esetek láthatóak.
esetek láthatóak.
A cikk elején feltett kérdés természetesen felvetődik egy általános norma esetén is, ekkor a kérdés a következőképp hangzik. Tekintsünk egy ![]() normát
normát ![]() -on és tegyük fel, hogy adott négy pont a térben,
-on és tegyük fel, hogy adott négy pont a térben, ![]() és
és ![]() . Elegendő információt ad-e a négy
. Elegendő információt ad-e a négy ![]() távolság ahhoz, hogy a térben bármely
távolság ahhoz, hogy a térben bármely ![]() pontot egyértelműen meg tudjunk határozni? (Hasonló a kérdés
pontot egyértelműen meg tudjunk határozni? (Hasonló a kérdés ![]() -n három ponttal). Mivel már az euklideszi esetben is fel kellett tennünk, hogy
-n három ponttal). Mivel már az euklideszi esetben is fel kellett tennünk, hogy ![]() és
és ![]() nem egy síkra esik (hasonlóan
nem egy síkra esik (hasonlóan ![]() -n, hogy
-n, hogy ![]() és
és ![]() nem esik egy egyenesre), mostantól kezdve ezt a cikkben mindig automatikusan fel fogjuk tenni! Mint azt látni fogjuk, általában még ekkor sem elegendő a négy távolság ismerete ahhoz, hogy minden
nem esik egy egyenesre), mostantól kezdve ezt a cikkben mindig automatikusan fel fogjuk tenni! Mint azt látni fogjuk, általában még ekkor sem elegendő a négy távolság ismerete ahhoz, hogy minden ![]() pontot meg tudjunk határozni a térben. (Megjegyezzük, hogy bár minden esetben bizonyos pontok pozícionálásához ez a négy távolság elegendő, mi ezt minden pontra megköveteljük). Ahhoz hogy ennek okát lássuk, a „fordított gondolatmenetet” fogjuk alkalmazni a normára, de előbb bevezetünk egy fogalmat. Legyen
pontot meg tudjunk határozni a térben. (Megjegyezzük, hogy bár minden esetben bizonyos pontok pozícionálásához ez a négy távolság elegendő, mi ezt minden pontra megköveteljük). Ahhoz hogy ennek okát lássuk, a „fordított gondolatmenetet” fogjuk alkalmazni a normára, de előbb bevezetünk egy fogalmat. Legyen ![]() és
és ![]() két különböző pont a térben, ekkor a
két különböző pont a térben, ekkor a
halmazt az ![]() és
és ![]() biszektorának hívjuk. Az euklideszi esetben ez egy sík volt (egyenes a sík esetében).
biszektorának hívjuk. Az euklideszi esetben ez egy sík volt (egyenes a sík esetében).
Az euklideszi esetben már elmagyarázott gondolatmenethez hasonlóan kapjuk, hogy az ![]() és
és ![]() pontokat pontosan akkor nem különbözteti meg a
pontokat pontosan akkor nem különbözteti meg a ![]() és
és ![]() (
(![]() ) távolságok ismerete, ha a
) távolságok ismerete, ha a ![]() és
és ![]() pontok a
pontok a ![]() biszektorra esnek. Következésképpen, a
biszektorra esnek. Következésképpen, a ![]() távolságok ismerete pontosan akkor elegendő minden
távolságok ismerete pontosan akkor elegendő minden ![]() pont pozícionálásához a térben, ha nem létezik két olyan különböző
pont pozícionálásához a térben, ha nem létezik két olyan különböző ![]() és
és ![]() pont, amelyek
pont, amelyek ![]() biszektorára a
biszektorára a ![]() és
és ![]() pontok esnek.
pontok esnek.
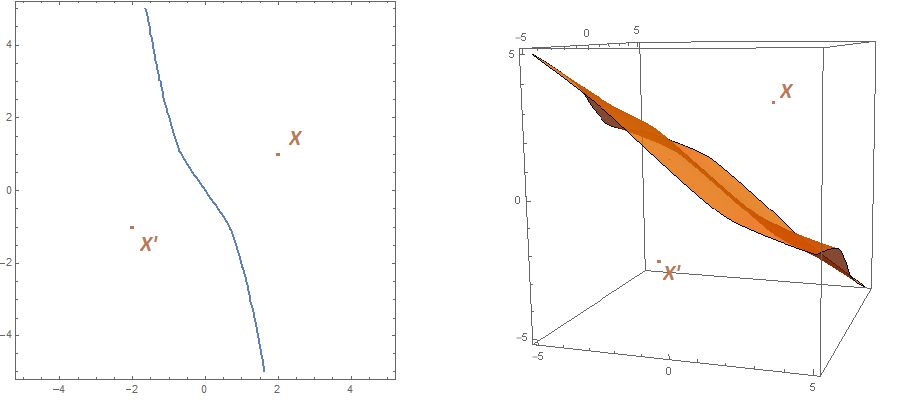
4. ábra. Egy-egy biszektor a síkon és a térben ![]() -norma esetén,
-norma esetén, ![]() .
.
A fentiek alapján pontosan akkor lenne bármely nem egy síkra eső pontnégyes megfelelő a mi célunknak, ha minden biszektor egy sík lenne (egyenes ![]() -n). Ismert eredmény, hogy ez pontosan akkor történik, ha a norma euklideszi, azaz ha a norma belső szorzatból származtatható. A híres Jordan—von Neumann-tétel miatt ez ekvivalens azzal, hogy a norma teljesíti a parallelogramma-azonosságot, azaz ha
-n). Ismert eredmény, hogy ez pontosan akkor történik, ha a norma euklideszi, azaz ha a norma belső szorzatból származtatható. A híres Jordan—von Neumann-tétel miatt ez ekvivalens azzal, hogy a norma teljesíti a parallelogramma-azonosságot, azaz ha
teljesül minden ![]() esetén.
esetén.
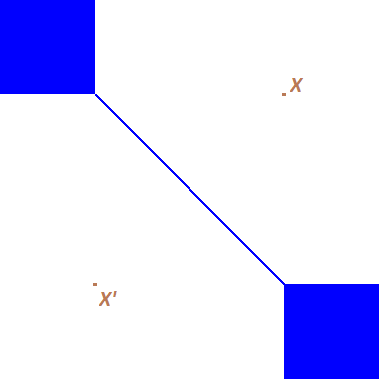
5. ábra. Biszektor a síkon az 1-norma (Manhattan norma) esetén
Egy biszektor igen különösen is viselkedhet, például bizonyos normák esetén nem mindig ad egy kétdimenziós felületet (a síkon pedig nem mindig egy görbét). Ismert, hogy ez a jelenség nem fordul elő, ha az egységgömb határa nem tartalmaz (nem elfajuló) szakaszt, amely esetben a normát szigorúan konvexnek hívjuk. A fenti ![]() -normák a
-normák a ![]() esetben szigorúan konvexek, ezért akkor minden biszektor egy kétdimenziós felület (görbe a síkon). A 4. ábra egy-egy példát mutat ilyen biszektorra a síkon és a térben. A
esetben szigorúan konvexek, ezért akkor minden biszektor egy kétdimenziós felület (görbe a síkon). A 4. ábra egy-egy példát mutat ilyen biszektorra a síkon és a térben. A ![]() esetekben viszont vannak olyan biszektorok, amelyeknek belseje nem üres, s így nem kétdimenziós felület a térben, vagy nem egy görbe a síkon (lásd az 5. ábrát). Megjegyezzük, hogy létezik olyan norma
esetekben viszont vannak olyan biszektorok, amelyeknek belseje nem üres, s így nem kétdimenziós felület a térben, vagy nem egy görbe a síkon (lásd az 5. ábrát). Megjegyezzük, hogy létezik olyan norma ![]() -on, amely nem szigorúan konvex, mégis minden biszektor egy kétdimenziós felületet ad. Erre az érdekes tényre először G. Horváth Ákos (BME Geometria Tanszék) mutatott rá egyik 2000-ben írt publikációjában.
-on, amely nem szigorúan konvex, mégis minden biszektor egy kétdimenziós felületet ad. Erre az érdekes tényre először G. Horváth Ákos (BME Geometria Tanszék) mutatott rá egyik 2000-ben írt publikációjában.
Természetesen adódhat a kérdés, hogy mi történik akkor, ha nem akarunk minden pontot meghatározni a négy távolsággal, hanem csak a ![]() és
és ![]() pontok által feszített tetraéderben található pontokra akarjuk ezt megtenni (háromszög a síkon). Erre a kérdésre a válasz csak 2016-ban született meg. Ez esetben nagy különbség van a sík és a három dimenziós tér között. A sík esetében az derül ki, hogy ha
pontok által feszített tetraéderben található pontokra akarjuk ezt megtenni (háromszög a síkon). Erre a kérdésre a válasz csak 2016-ban született meg. Ez esetben nagy különbség van a sík és a három dimenziós tér között. A sík esetében az derül ki, hogy ha ![]() a
a ![]() és
és ![]() által feszített háromszögön fekszik és a norma szigorúan konvex, akkor
által feszített háromszögön fekszik és a norma szigorúan konvex, akkor ![]() helyzete mindig pontosan meghatározható a
helyzete mindig pontosan meghatározható a ,
és
távolságok ismeretében, illetve az állítás megfordítása is igaz (lásd a 6. ábrát). A térben viszont ez már nem így van! Pontosabban az derül ki, hogy ha a norma nem Euklideszi, akkor mindig található négy olyan
![]() és
és ![]() pont és két másik
pont és két másik ![]() pont, amelyek a négy pont által feszített tetraéderben vannak és teljesülnek a
pont, amelyek a négy pont által feszített tetraéderben vannak és teljesülnek a ![]() egyenletek minden
egyenletek minden ![]() -re (lásd a 7. ábrát). Tehát általában egy tetraéderben fekvő pont helyzete nem határozható meg a csúcsoktól mért nem euklideszi távolságok ismeretében. A tétel bizonyítása a biszektorok geometriai vizsgálatán alapul, amely a háromdimenziós esetben projektív geometriai eszközöket kíván.
-re (lásd a 7. ábrát). Tehát általában egy tetraéderben fekvő pont helyzete nem határozható meg a csúcsoktól mért nem euklideszi távolságok ismeretében. A tétel bizonyítása a biszektorok geometriai vizsgálatán alapul, amely a háromdimenziós esetben projektív geometriai eszközöket kíván.
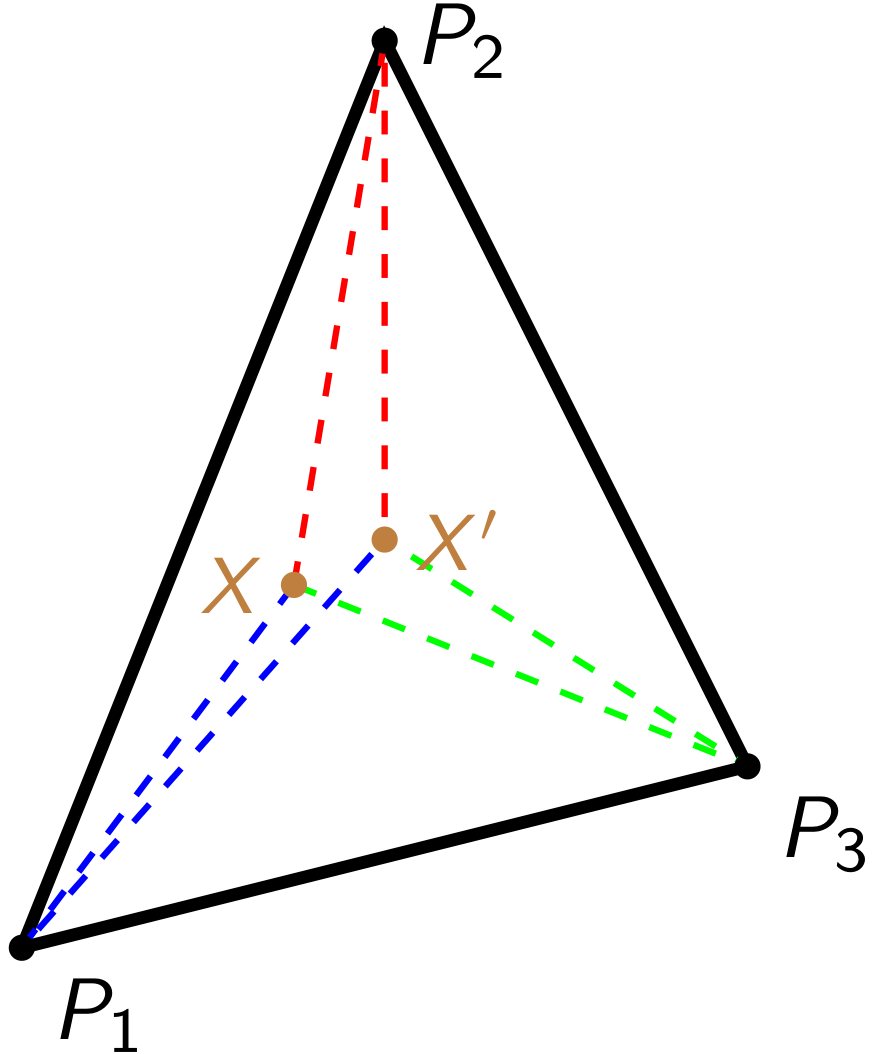
6. ábra. Ez csak akkor történhet meg, ha a norma nem szigorúan konvex. A színes szaggatott vonalak azt jelzik, hogy az adott távolságok megegyeznek.
Végül megjegyezzük, hogy a fenti problémák tárgyalása az általánosabb ![]() -dimenziós esetben is lehetséges, itt csupán a szemléletesség kedvéért szorítkoztunk a két-, illetve háromdimenziós esetekre.
-dimenziós esetben is lehetséges, itt csupán a szemléletesség kedvéért szorítkoztunk a két-, illetve háromdimenziós esetekre.
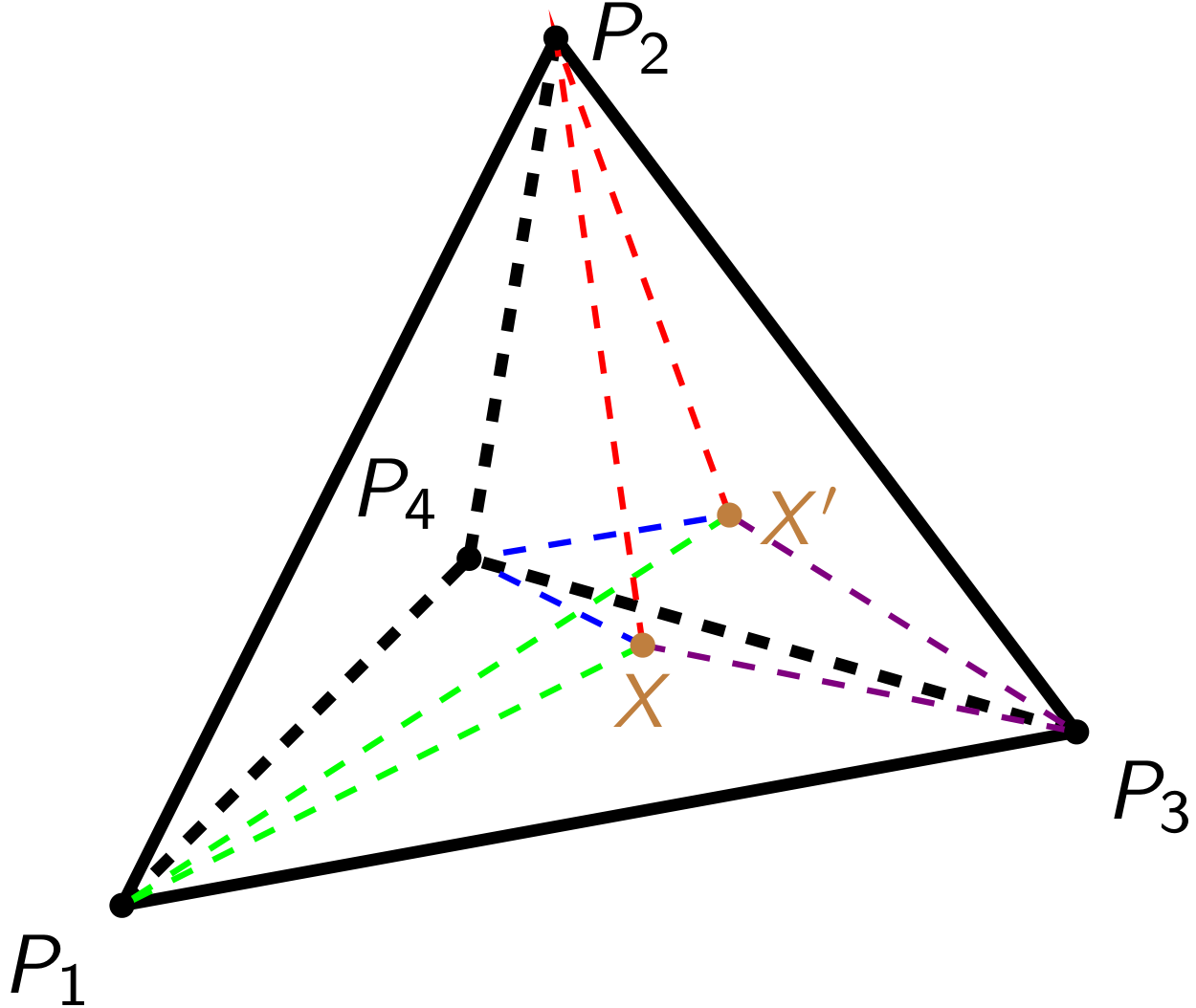
7. ábra. Ez viszont megtörténhet, ha a norma nem euklideszi. A színes szaggatott vonalak azt jelzik, hogy az adott távolságok megegyeznek.









