A Legendre-csomók elmélete az általános csomóelmélet és a kontakt topológia egy határterülete. Legendre-csomókkal akkor találkozunk, amikor a kontakt topológia extra struktúrájával együtt vizsgálunk általános csomókat, vagy amikor csomóelméleti ötleteket használunk fel a kontakt topológia, illetve alkalmazásainak megértéséhez. Írásunkban először bemutatjuk, mik is a Legendre-csomók, majd motivációt adunk tanulmányozásukhoz.
Egy (általános/sima) csomó a körvonal egy sima beágyazása ![]() -ba (vagy bármilyen más 3-sokaságba, de ebben a cikkben elsősorban
-ba (vagy bármilyen más 3-sokaságba, de ebben a cikkben elsősorban ![]() -mal foglalkozunk). Egy kontakt struktúra egy speciális típusú síkmező – ahogy egy vektormező a tér minden pontjában megad egy vektort, egy síkmező minden ponthoz egy egész síkot rendel. Az 1. ábrán a sztenderd kontakt struktúra,
-mal foglalkozunk). Egy kontakt struktúra egy speciális típusú síkmező – ahogy egy vektormező a tér minden pontjában megad egy vektort, egy síkmező minden ponthoz egy egész síkot rendel. Az 1. ábrán a sztenderd kontakt struktúra, ![]() látható
látható ![]() -on, amit alább részletesebben is bemutatunk majd. Bár precízen nem definiáljuk a kontakt struktúrákat, a fogalom lényege az, hogy a kontakt struktúra síkjai úgy forognak, hogy nem létezhet olyan felület, amelynek érintői mind részei a kontakt síkmezőnek. Ennek ellenére vannak olyan görbék, amelyek érintővektorai belesimulnak a kontakt struktúrába; az ilyen görbéket nevezzük Legendre-típusúnak. Az olyan csomók, amelyek egyben Legendre-típusú görbék is, a Legendre-csomók.
-on, amit alább részletesebben is bemutatunk majd. Bár precízen nem definiáljuk a kontakt struktúrákat, a fogalom lényege az, hogy a kontakt struktúra síkjai úgy forognak, hogy nem létezhet olyan felület, amelynek érintői mind részei a kontakt síkmezőnek. Ennek ellenére vannak olyan görbék, amelyek érintővektorai belesimulnak a kontakt struktúrába; az ilyen görbéket nevezzük Legendre-típusúnak. Az olyan csomók, amelyek egyben Legendre-típusú görbék is, a Legendre-csomók.
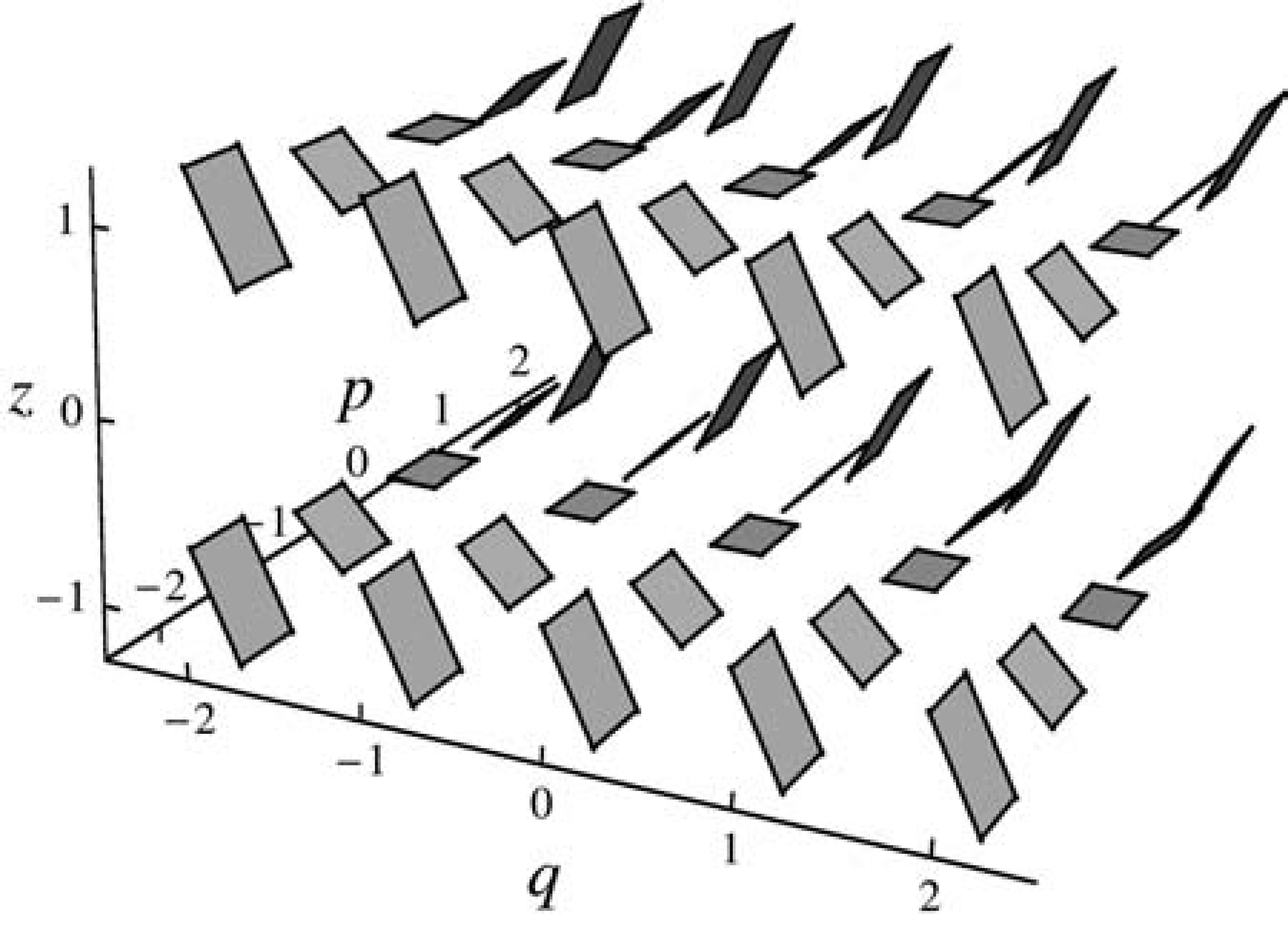
1.ábra. A sztenderd kontakt struktúra ![]() -on (az ábra Mathematica használatával készült).
-on (az ábra Mathematica használatával készült).
A továbbiakban ![]() -ban, a sztenderd kontakt térben vizsgálunk Legendre-csomókat. Hogy megértsük a sztenderd kontakt struktúrát, először képzeljünk el egy egykerekűt például egy parkolóban, majd tekintsük a pályát, amit az egykerekű járna be azzal a megkötéssel, hogy a kerék sosem áll észak-déli irányba. Az egykerekű helyzete
-ban, a sztenderd kontakt térben vizsgálunk Legendre-csomókat. Hogy megértsük a sztenderd kontakt struktúrát, először képzeljünk el egy egykerekűt például egy parkolóban, majd tekintsük a pályát, amit az egykerekű járna be azzal a megkötéssel, hogy a kerék sosem áll észak-déli irányba. Az egykerekű helyzete ![]() -ban leírható a
-ban leírható a ![]() koordinátákkal, ahol
koordinátákkal, ahol ![]() az egykerekű pozíciója a parkolóban,
az egykerekű pozíciója a parkolóban, ![]() pedig a kerék
pedig a kerék ![]() és
és ![]() tengelyekre vonatkozó meredeksége, fentről nézve. Az egykerekű bármelyik pillanatban helyben elfordulhat, elmozdulhat előre vagy hátra – abba az irányba, amelybe a kereke néz –, vagy megteheti ezen mozgások tetszőleges lineáris kombinációját. Ekkor az egykerekű pályáját leíró
tengelyekre vonatkozó meredeksége, fentről nézve. Az egykerekű bármelyik pillanatban helyben elfordulhat, elmozdulhat előre vagy hátra – abba az irányba, amelybe a kereke néz –, vagy megteheti ezen mozgások tetszőleges lineáris kombinációját. Ekkor az egykerekű pályáját leíró ![]() görbe érinti a
görbe érinti a ![]() és
és ![]() vektormezők által kifeszített síkmezőt, így kielégíti a következő egyenletet:
vektormezők által kifeszített síkmezőt, így kielégíti a következő egyenletet:
| (1) |
Ez a síkmező a korábban említett sztenderd kontakt struktúra, amiben a ![]() görbe Legendre-típusú.
görbe Legendre-típusú.
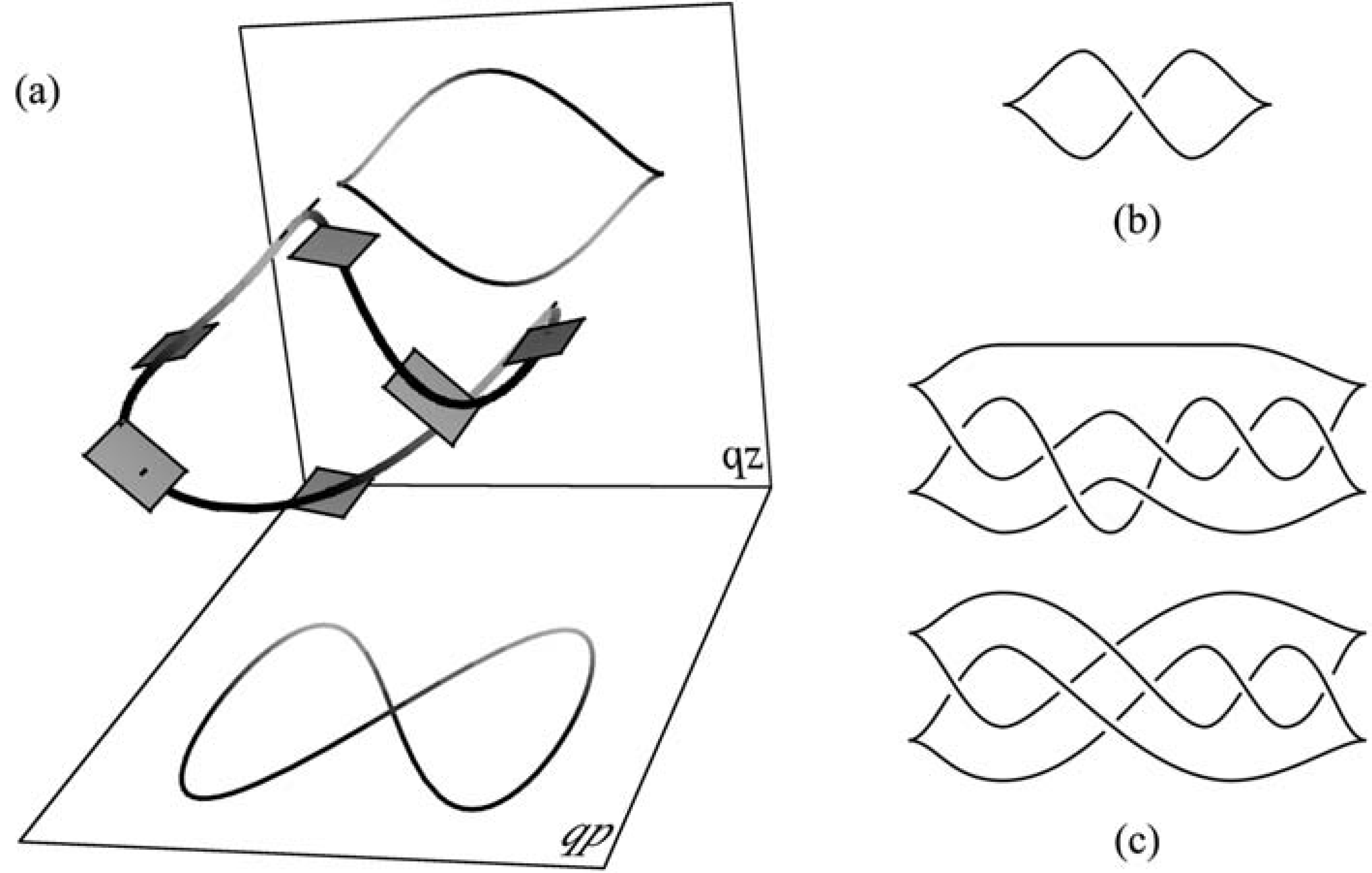
2. ábra. (a) Legendre-típusú triviális csomó hátul a frontális, lent a Lagrange-vetületével; (b) Egy másik Legendre-típusú triviális csomó frontális vetülete; (c) A Chekanov–Eliashberg példák
A feltétel, amit az (1) egyenlet jelent a csomóra nézve, a ![]() és
és ![]() síkokra való vetületen a legszemléletesebb, ezeket mutatja a 2. ábra. Az (1) egyenlet szerint egy Legendre-típusú görbe
síkokra való vetületen a legszemléletesebb, ezeket mutatja a 2. ábra. Az (1) egyenlet szerint egy Legendre-típusú görbe ![]() koordinátáját egyértelműen meghatározza a görbe
koordinátáját egyértelműen meghatározza a görbe ![]() síkra vett frontális (elülső) vetületének meredeksége. Az egykerekű példájánál maradva a frontális vetület a parkolóban hagyott keréknyom. A 2. ábrán néhány Legendre-csomó frontális vetülete látható.
síkra vett frontális (elülső) vetületének meredeksége. Az egykerekű példájánál maradva a frontális vetület a parkolóban hagyott keréknyom. A 2. ábrán néhány Legendre-csomó frontális vetülete látható.
Figyeljük meg, hogy a vetületen minden kereszteződés ugyanúgy néz ki: a kisebb meredekségű ív halad el a nagyobb meredekségű fölött. Minden olyan ![]() síkbeli zárt görbe, amely véges sok „csúcsos”, úgynevezett cusp kivételtől eltekintve immerzió, és nincsenek függőleges érintői, előáll egy Legendre-csomó frontális vetületeként.
síkbeli zárt görbe, amely véges sok „csúcsos”, úgynevezett cusp kivételtől eltekintve immerzió, és nincsenek függőleges érintői, előáll egy Legendre-csomó frontális vetületeként.
Az (1) egyenletből az is következik, hogy egy Legendre-típusú görbe ![]() koordinátája (konstans erejéig) egyértelműen meghatározható a
koordinátája (konstans erejéig) egyértelműen meghatározható a ![]() mennyiség integrálásával a görbe
mennyiség integrálásával a görbe ![]() síkra vett, úgynevezett Lagrange-vetülete mentén. Mivel egy csomón végighaladva annak
síkra vett, úgynevezett Lagrange-vetülete mentén. Mivel egy csomón végighaladva annak ![]() koordinátája vissza kell térjen a kiindulási értékébe, Green tétele szerint egy Legendre-csomó Lagrange-vetülete nulla előjeles területű részt határol. Tehát a sima körvonal nem lehet egy Legendre-csomó Lagrange-vetülete.
koordinátája vissza kell térjen a kiindulási értékébe, Green tétele szerint egy Legendre-csomó Lagrange-vetülete nulla előjeles területű részt határol. Tehát a sima körvonal nem lehet egy Legendre-csomó Lagrange-vetülete.
A csomóelmélet két alapvető célja, hogy megértsük a csomók „geográfiáját” – azaz hogy megkülönböztessük, avagy osztályozzuk a csomókat –, és hogy tanulmányozzuk a csomó helyzetét a háromdimenziós térben. E célkitűzések vonatkoznak a Legendre-csomóelméletre is. Két sima csomót ekvivalensnek tekintünk, ha sima mozgatásokkal, sima csomókon keresztül egymásba vihetők; hasonlóan, két Legendre-csomó ekvivalens, ha egymásba mozgathatók Legendre-csomókon keresztül.
Két ekvivalens Legendre-csomó sima csomóként is ekvivalens egymással, ám ez fordítva nem igaz. Hogy erről meggyőződhessünk, bevezetünk két „klasszikus” invariánst.
A Thurston–Bennequin-szám a Legendre-csomó, és annak egy olyan (például a ![]() irányba) eltolt példányának hurkolódási számát méri, amely mindenhol transzverzálisan metszi
irányba) eltolt példányának hurkolódási számát méri, amely mindenhol transzverzálisan metszi ![]() -t.
-t.
A 2. (a) ábrán lévő csomó Thurston–Benneqin-száma ![]() , míg a 2. (b) ábrán lévő (szintén triviális!) csomóé
, míg a 2. (b) ábrán lévő (szintén triviális!) csomóé ![]() . A rotációs szám egy irányított Legendre-csomó Lagrange-vetületén méri az érintővektorok körülfordulási számát. Ez is megkülönbözteti a 2. (a) és (b) ábrák csomóit.
. A rotációs szám egy irányított Legendre-csomó Lagrange-vetületén méri az érintővektorok körülfordulási számát. Ez is megkülönbözteti a 2. (a) és (b) ábrák csomóit.
A klasszikus invariánsok segítségével pontosíthatjuk a Legendre-csomók helyzetének kérdését egy rögzített sima csomóosztályon belül: Mely ![]() invariánspárok realizálhatók Legendre-csomóval, és hány Legendre-csomóosztály rendelkezik azonos klasszikus invariánspárral?
invariánspárok realizálhatók Legendre-csomóval, és hány Legendre-csomóosztály rendelkezik azonos klasszikus invariánspárral?
A triviális csomóra Eliashberg és Fraser bizonyították, hogy pontosan az olyan ![]() párok érhetők el, amelyek tagjai ellentétes paritásúak, valamint kielégítik a
párok érhetők el, amelyek tagjai ellentétes paritásúak, valamint kielégítik a ![]() Benneqin-korlátot; és hogy minden ilyen invariánspárhoz pontosan egy Legendre-csomóosztály tartozik. Eszerint minden Legendre-típusú triviális csomó előállítható a 2. (a) ábra frontális diagramjából néhány cikkcakk hozzáadásával (ezt a műveletet stabilizációnak nevezzük).
Benneqin-korlátot; és hogy minden ilyen invariánspárhoz pontosan egy Legendre-csomóosztály tartozik. Eszerint minden Legendre-típusú triviális csomó előállítható a 2. (a) ábra frontális diagramjából néhány cikkcakk hozzáadásával (ezt a műveletet stabilizációnak nevezzük).
Tóruszcsomókra, a 8-as csomóra, és egyes tóruszláncokra hasonló osztályozás ismert, de a helyzet általában bonyolultabb: Eliashberg és Chekanov felfedezte, hogy a 2. (c) ábrán látható két Legendre-csomó azonos csomóosztályhoz tartozik, invariánsaik ![]() és
és ![]() , mégsem ekvivalensek. Számos olyan „nem klasszikus” invariánst ismerünk, amely képes megkülönböztetni ezeket (illetve más csomókat) is: ilyen a Legendre-féle kontakt homológia, mely speciális esete Eliashberg, Givental és Hofer szimplektikus mezőelméletének (Symplectic Field Theory); Chekanov, Pushkar és Traynor generátorcsalád-elmélete; vagy Ozsváth, Szabó és Thurston Legendre-invariánsa a csomó-Floer-homológiában. Ezek az újonnan kifejlesztett invariánsok a Legendre-csomók, illetve komplementumuk olyan finom kontakt topológiai tulajdonságait is ki tudják mutatni, amelyekről alkotott képünk csak napjainkban kezd kirajzolódni.
, mégsem ekvivalensek. Számos olyan „nem klasszikus” invariánst ismerünk, amely képes megkülönböztetni ezeket (illetve más csomókat) is: ilyen a Legendre-féle kontakt homológia, mely speciális esete Eliashberg, Givental és Hofer szimplektikus mezőelméletének (Symplectic Field Theory); Chekanov, Pushkar és Traynor generátorcsalád-elmélete; vagy Ozsváth, Szabó és Thurston Legendre-invariánsa a csomó-Floer-homológiában. Ezek az újonnan kifejlesztett invariánsok a Legendre-csomók, illetve komplementumuk olyan finom kontakt topológiai tulajdonságait is ki tudják mutatni, amelyekről alkotott képünk csak napjainkban kezd kirajzolódni.
A Legendre-csomók nemcsak önmagukért érdekesek, hanem egyben eszközöket szolgáltatnak a kontakt topológia és a csomóelmélet tanulmányozásához. Kontakt topológiában gyakran Legendre-csomók segítségével vizsgáljuk a környező kontakt struktúrát. Erre az első példát Benneqin szolgáltatta az ![]() -on lévő
-on lévő ![]() „egzotikus” kontakt struktúra felfedezésekor: olyan Legendre-típusú triviális csomót talált
„egzotikus” kontakt struktúra felfedezésekor: olyan Legendre-típusú triviális csomót talált ![]() -ben, amelyre nem teljesült a Benneqin-korlát, így különböztetve meg
-ben, amelyre nem teljesült a Benneqin-korlát, így különböztetve meg ![]() -t
-t ![]() -tól. Legendre-csomókat használunk új kontakt sokaságok létrehozásakor is, a műtétek leírásához.
-tól. Legendre-csomókat használunk új kontakt sokaságok létrehozásakor is, a műtétek leírásához.
A Legendre-csomók elméletének fejlődése nagy hatással van a sima csomóelméletre is, hiszen szoros kapcsolatban állnak az ismert geometriai (4-génusz) és kvantum (HOMFLY, Kauffman, Khovanov, …) csomóinvariánsokkal, valamint alkalmazhatók olyan új invariánsok megalkotásánál, mint például Ng csomó kontakt homológiája, ami magasabb dimenziós Legendre-csomókat használ. Mindemellett a Legendre-csomók (illetve az ezekkel analóg módon definiálható, a kontakt struktúrát mindenhol transzverzálisan metsző csomók) mentén végzett műtétek jelentős szerepet játszottak Kronheimer és Mrowka bizonyításában, amikor igazolták, hogy minden nemtriviális csomóra fennáll a P tulajdonság.
Nemrég Chekanov és Pushkar az Arnold-féle „4 cusp” sejtésre adott bizonyításukban ismét eredeti környezetükben, a geometriai optikában alkalmazta a Legendre-csomókat (hullámfrontokként).
Mindezek ellenére a Legendre-csomók geográfiájának, geometriájának és alkalmazásainak megértéséhez vezető útnak csupán a legelején járunk.
Irodalomjegyzék
- [1] D. Bennequin, Entrelacements et équations de Pfaff, Asterisque 107–108 (1983), 87–161.
- [2] J. Etnyre, Legendrian and Transversal Knots, Handbook of Knot Theory, Elsevier, 2005, pp. 105–185.
- [3] H. Geiges, An Introduction to Contact Topology, Cambridge Studies in Advanced Mathematics, 109, Cambridge University Press, 2008.
Joshua M. Sabloff, Harverdord College
A cikk az Amerikai Matematikai Társaság Notices folyóiratának 2009. novemberi számában jelent meg, ezúton köszönjük az AMS és a szerző szíves engedélyét a fordítás közléséhez. Fordította: Földvári Viktória.
Joshua M. Sabloff, “What is...a Legendrian Knot?” Notices Amer. Math. Soc. 56, No. 10 (November 2009) 1282-84. ©2009 American Mathematical Society.









