A Wasserstein-terek olyan speciális metrikus terek, amelynek pontjai valószínűségi mértékek, a pontok közötti távolságot pedig transzport tervek segítségével lehet meghatározni. Ilyen módon ez a cikk az előző számban megjelent „Mi is a... Monge-Kantorovics probléma” című írás folytatása.
Rávilágítandó a transzportelmélet eszközeinek erejére, vázlatosan bemutatjuk a 2018-ban Fields-éremmel kitüntetett Alessio Figalli egyik optimális transzportot használó eredményét. Ezek után néhány motiváló példa érintésével eljutunk az ![]() -re épített Wasserstein-terek definíciójáig. Ugyan az
-re épített Wasserstein-terek definíciójáig. Ugyan az ![]() -nél komplikáltabb terekre is lehetne építkezni, és a definíciók sem lennének sokkal bonyolultabbak, mi megelégszünk ezzel az általánossággal. A Wasserstein-tér néhány érdekes tulajdonságának bemutatása után a cikket egy alkalmazással zárjuk: vázolunk egy eljárást, aminek segítségével egy képet fel lehet ruházni egy másik kép stílusjegyeivel.
-nél komplikáltabb terekre is lehetne építkezni, és a definíciók sem lennének sokkal bonyolultabbak, mi megelégszünk ezzel az általánossággal. A Wasserstein-tér néhány érdekes tulajdonságának bemutatása után a cikket egy alkalmazással zárjuk: vázolunk egy eljárást, aminek segítségével egy képet fel lehet ruházni egy másik kép stílusjegyeivel.
1. Az izoperimetrikus egyenlőtlenség és alkalmazásai
Mielőtt rátérünk Figalli és szerzőtársainak eredményére, röviden felidézünk néhány alapfogalmat. Az ![]() tér bizonyos részhalmazait akarjuk majd megmérni, természetes kívánalom, hogy az olyan egyszerű halmazok, mint a gömbök mérhetőek legyenek. Emlékeztetünk, hogy az
tér bizonyos részhalmazait akarjuk majd megmérni, természetes kívánalom, hogy az olyan egyszerű halmazok, mint a gömbök mérhetőek legyenek. Emlékeztetünk, hogy az ![]() középpontú
középpontú ![]() sugarú nyílt gömb nem más, mint
sugarú nyílt gömb nem más, mint ![]() , ahol
, ahol ![]() ,
, ![]() és
és 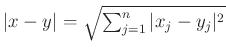 .
.
Jelölje ![]() a legszűkebb olyan halmazrendszert, amely
a legszűkebb olyan halmazrendszert, amely
– tartalmazza az összes nyílt gömböt,
– zárt a komplementer képzésére, azaz ha tartalmazza ![]() -t, akkor tartalmazza
-t, akkor tartalmazza ![]() -t is,
-t is,
– ha tartalmazza egy ![]() sorozat minden tagját, akkor tartalmazza az egyesítésüket is.
sorozat minden tagját, akkor tartalmazza az egyesítésüket is.
Ezt a ![]() halmazrendszert az
halmazrendszert az ![]() metrikus tér Borel
metrikus tér Borel ![]() -algebrájának nevezzük. A
-algebrájának nevezzük. A ![]() halmazfüggvény egy Borel valószínűségi mérték, ha
halmazfüggvény egy Borel valószínűségi mérték, ha
a) ![]() és
és
b) ha ![]() egy olyan
egy olyan ![]() -ben haladó halmazsorozat, hogy
-ben haladó halmazsorozat, hogy ![]() esetén
esetén ![]() , akkor
, akkor 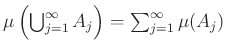 .
.
Az összes Borel valószínűségi mérték halmazát mostantól ![]() -nel jelöljük. Külön kiemeljük a
-nel jelöljük. Külön kiemeljük a ![]() halmaz két fontos részhalmazát: a Dirac-mértékek
halmaz két fontos részhalmazát: a Dirac-mértékek ![]() halmazát, és azok véges konvex kombinációinak
halmazát, és azok véges konvex kombinációinak ![]() halmazát. Emlékeztetünk, hogy az
halmazát. Emlékeztetünk, hogy az ![]() pontra koncentrált Dirac-mérték definíciója:
pontra koncentrált Dirac-mérték definíciója: ![]() ha
ha ![]() , és
, és ![]() ha
ha ![]() . Ebben a cikkben mindig Borel-mértékekkel dolgozunk, ezért a továbbiakban a Borel szót sem a mértékek, sem pedig a mérhető halmazok elé nem tesszük ki.
. Ebben a cikkben mindig Borel-mértékekkel dolgozunk, ezért a továbbiakban a Borel szót sem a mértékek, sem pedig a mérhető halmazok elé nem tesszük ki.
Felidézzük a transzportelmélet néhány alapfogalmát is. Tegyük fel, hogy adott egy folytonos ![]() költségfüggvény, és két valószínűségi mérték
költségfüggvény, és két valószínűségi mérték ![]() . Olyan
. Olyan ![]() mérhető függvényt keresünk, amelyre
mérhető függvényt keresünk, amelyre
teljesül minden ![]() mérhető halmaz esetén. Ilyenkor a
mérhető halmaz esetén. Ilyenkor a ![]() -t transzport leképezésnek,
-t transzport leképezésnek, ![]() -t pedig a
-t pedig a ![]()
![]() -szerinti előretoltjának neveztük. Egy ilyen
-szerinti előretoltjának neveztük. Egy ilyen ![]() függvény mentén a teljes transzport költsége
függvény mentén a teljes transzport költsége

Ilyen ![]() függvény persze nem feltétlenül létezik. A probléma Kantorovics-féle megfogalmazásában transzport terveket keresünk, azaz olyan
függvény persze nem feltétlenül létezik. A probléma Kantorovics-féle megfogalmazásában transzport terveket keresünk, azaz olyan ![]() valószínűségi mértékeket az
valószínűségi mértékeket az ![]() szorzat téren, amelyeknek marginálisai
szorzat téren, amelyeknek marginálisai ![]() és
és ![]() . A transzport tervek halmazát
. A transzport tervek halmazát ![]() -vel jelöljük.
-vel jelöljük.
Megjegyzendő, hogy ![]() soha nem üres, ugyanis
soha nem üres, ugyanis ![]() és
és ![]() szorzatmértéke megfelel a kritériumnak. Láttuk, hogy egy
szorzatmértéke megfelel a kritériumnak. Láttuk, hogy egy ![]() transzport terv költsége
transzport terv költsége

Ki fog derülni, hogy a Wasserstein-tér definíciójához pontosan ezekre a fogalmakra van szükségünk abban a speciális esetben, amikor a ![]() költségfüggvény a távolság egy hatványával egyezik meg.
költségfüggvény a távolság egy hatványával egyezik meg.
Most rátérünk Alessio Figalli és szerzőtársainak egy érdekes eredményére. Tudománynépszerűsítő előadásaiban Figalli a problémát Dido legendájával vezeti fel, ezt tesszük mi is. A legenda szerint Iarbás király (Jupiter istenség és Garamantis nimfa fia) annyi területet engedett át országából a Pygmalion zsarnoksága elől meneküló Didónak és követőinek, amennyit egy ökör bőre körülölel. Dido ravasz módon vékony csíkokra vágta a bőrt, és körülkerítette azt a dombot, ahová később Karthago fellegvára épült. De mi köze ennek az izoperimetrikus egyenlőtlenséghez?
Az izoperimetrikus egyenlőtlenség a síkon azt mondja, hogy ha egy egyszerű zárt rektifikálható görbe kerülete ![]() , az általa körbekerített terület pedig
, az általa körbekerített terület pedig ![]() , akkor
, akkor ![]() . Egyenlőség csak akkor teljesül, ha a szóban forgó görbe a körvonal. Hasonló egyenlőtlenség magasabb dimenzióban is felírható a térfogattal és a felülettel.
. Egyenlőség csak akkor teljesül, ha a szóban forgó görbe a körvonal. Hasonló egyenlőtlenség magasabb dimenzióban is felírható a térfogattal és a felülettel.
Mostantól az egyszerűség kedvéért mindig nagyon szép halmazokkal dolgozunk. Ha azt mondjuk, hogy legyen ![]() , akkor mindig egy korlátos és egyszeresen összefüggő tartományra gondolunk, aminek sima a határa. A
, akkor mindig egy korlátos és egyszeresen összefüggő tartományra gondolunk, aminek sima a határa. A ![]() jelölést olyan korlátos konvex nyílt halmazokra tartjuk fenn, amelyek tartalmazzák az origót. Az origó középpontú egység sugarú nyílt gömböt pedig
jelölést olyan korlátos konvex nyílt halmazokra tartjuk fenn, amelyek tartalmazzák az origót. Az origó középpontú egység sugarú nyílt gömböt pedig ![]() -vel jelöljük.
-vel jelöljük.
Az ![]() halmaz térfogatát
halmaz térfogatát ![]() -vel, felszínét (periméterét) pedig
-vel, felszínét (periméterét) pedig ![]() -vel jelöljük. Az
-vel jelöljük. Az ![]() -dimenziós perimetrikus egyenlőtlenség a következőképp szól:
-dimenziós perimetrikus egyenlőtlenség a következőképp szól:
Egyenlőség pontosan akkor áll fenn, ha ![]() egy gömb. Ennek az az oka, hogy a tér gömbje egy gömb. Hogy ezt hogy kell érteni, arra hamarosan fény derül. Most egy olyan módszerrel vezetjük be a
egy gömb. Ennek az az oka, hogy a tér gömbje egy gömb. Hogy ezt hogy kell érteni, arra hamarosan fény derül. Most egy olyan módszerrel vezetjük be a ![]() mennyiséget, ami egy fontos geometriai megfigyeléshez vezet. Jelölje
mennyiséget, ami egy fontos geometriai megfigyeléshez vezet. Jelölje ![]() az
az ![]() halmaz
halmaz ![]() -nal való felfújtját, azaz minden
-nal való felfújtját, azaz minden ![]() köré rakjunk egy
köré rakjunk egy ![]() sugarú gömböt. Minkowski-összegként ezt úgy írhatjuk, hogy
sugarú gömböt. Minkowski-összegként ezt úgy írhatjuk, hogy ![]() . Meg lehet mutatni, hogy ekkor
. Meg lehet mutatni, hogy ekkor
ahol az utolsó tag olyan kicsi, hogy még ![]() -nal osztva is eltűnik, és így
-nal osztva is eltűnik, és így
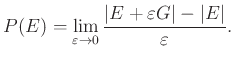
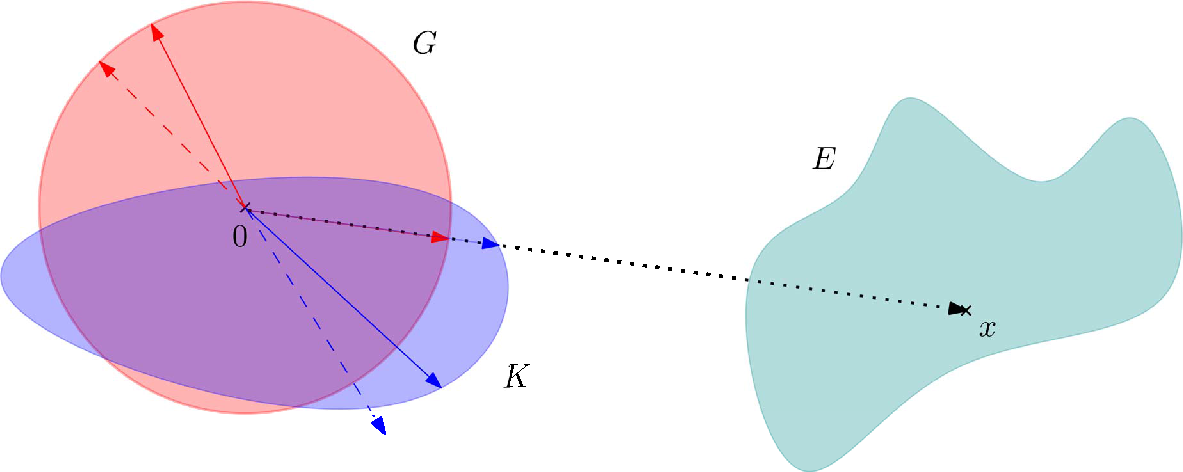
Magyarul a ![]() semmi mástól nem függ, mint
semmi mástól nem függ, mint ![]() -től és
-től és ![]() -től. Ez a felírás lehetőséget ad arra, hogy bevezessük az analóg fogalmat olyan terekben, amelyeknek tulajdonságai nem függetlenek az iránytól. Gondolhatunk arra, hogy egy fizikai jelenséget írunk le, és különböző irányokban különböző erők hatnak. A fenti 1. ábra azt mutatja, hogy ha a
-től. Ez a felírás lehetőséget ad arra, hogy bevezessük az analóg fogalmat olyan terekben, amelyeknek tulajdonságai nem függetlenek az iránytól. Gondolhatunk arra, hogy egy fizikai jelenséget írunk le, és különböző irányokban különböző erők hatnak. A fenti 1. ábra azt mutatja, hogy ha a ![]() gömböt lecseréljük
gömböt lecseréljük ![]() -ra, akkor az
-ra, akkor az ![]() vektor „hossza” kisebb lesz, hiszen
vektor „hossza” kisebb lesz, hiszen ![]() -t nem kell annyiszorosára fújni mint
-t nem kell annyiszorosára fújni mint ![]() -t, hogy az
-t, hogy az ![]() -et elnyelje. Továbbá előfordulhat, hogy egy origó körüli forgatással lemegyünk a gömbről. Ez azt mutatja, hogy a kék szaggatott nyíllal jelölt irányban máshogy skálázódik át hossz, mint a nem szaggatott kék nyíl irányában.
-et elnyelje. Továbbá előfordulhat, hogy egy origó körüli forgatással lemegyünk a gömbről. Ez azt mutatja, hogy a kék szaggatott nyíllal jelölt irányban máshogy skálázódik át hossz, mint a nem szaggatott kék nyíl irányában.
Mostantól tehát a gömb szerepét egy origót tartalmazó konvex nyílt ![]() halmaz játssza, a
halmaz játssza, a ![]() -szerinti perimétert pedig az alábbi formulával definiáljuk:
-szerinti perimétert pedig az alábbi formulával definiáljuk:

Wulff már 1901-ben megmutatta [16], hogy ebben az anizotróp környezetben is igaz az egyenlőtlenség, persze ![]() helyett
helyett ![]() -val
-val
Az egyenlőtlenség pontosan akkor teljesül egyenlőséggel, ha ![]() nagyítástól és eltolástól eltekintve megegyezik
nagyítástól és eltolástól eltekintve megegyezik ![]() -val, vagyis
-val, vagyis ![]() alkalmas
alkalmas ![]() -re és
-re és ![]() -ra. Tehát az derült ki, hogy az optimális konfigurációkat mindig a tér szerkezetét meghatározó (vagy ha úgy tetszik, a gömb szerepét betöltő)
-ra. Tehát az derült ki, hogy az optimális konfigurációkat mindig a tér szerkezetét meghatározó (vagy ha úgy tetszik, a gömb szerepét betöltő) ![]() halmaz adja. Ezt a
halmaz adja. Ezt a ![]() mennyiséget Wulff a felületi energia leírására alkalmazta kristályok egyensúlyi konfigurációjának tanulmányozásakor. Az egyensúlyi konfigurációt emiatt Wulff-alaknak nevezik. De hogy jön ide az optimális transzport?
mennyiséget Wulff a felületi energia leírására alkalmazta kristályok egyensúlyi konfigurációjának tanulmányozásakor. Az egyensúlyi konfigurációt emiatt Wulff-alaknak nevezik. De hogy jön ide az optimális transzport?
Figalliék a [4] cikkben megadták a fenti anizotróp egyenlőtlenségnek egy olyan bizonyítását, amelyik a transzportelmélet néhány nagyon mély eredményét használta. Ehhez először is mértékké kellett változtatni ![]() -t és
-t és ![]() -t:
-t:
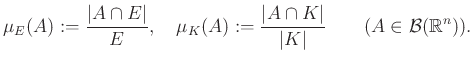
Tulajdonképpen ![]() -n és
-n és ![]() -n egyenletesen szétterítettünk egy-egy egységnyi tömeget. Amit kaptunk, az két olyan mérték, amihez Brenier és McCann nagyon szép eredményei (lásd [1,11,12]) szerint létezik
-n egyenletesen szétterítettünk egy-egy egységnyi tömeget. Amit kaptunk, az két olyan mérték, amihez Brenier és McCann nagyon szép eredményei (lásd [1,11,12]) szerint létezik ![]() transzport leképezés, ami átviszi
transzport leképezés, ami átviszi ![]() -t
-t ![]() -ba. Sőt, ez a
-ba. Sőt, ez a ![]() előáll, mint egy alkalmas
előáll, mint egy alkalmas ![]() konvex függvény gradiense. Tehát a transzportelmélet segítségével be lehetett hozni a képbe két függvényt
konvex függvény gradiense. Tehát a transzportelmélet segítségével be lehetett hozni a képbe két függvényt ![]() -t és
-t és ![]() -t, majd ezek segítségével meg tudtak becsülni néhány fontos mennyiséget. Így például az egyenlőtlenség két oldala közötti deficitet mérő
-t, majd ezek segítségével meg tudtak becsülni néhány fontos mennyiséget. Így például az egyenlőtlenség két oldala közötti deficitet mérő
mennyiséget, és az ![]() és
és ![]() alakjának eltérőségét mérő aszimmetriaindexet
alakjának eltérőségét mérő aszimmetriaindexet
Az ![]() definíciójában lévő
definíciójában lévő ![]() szimbólum a szimmetrikus differencia, tehát
szimbólum a szimmetrikus differencia, tehát
Megmutatták, hogy egy alkalmas ![]() -től függő
-től függő ![]() konstanssal
konstanssal
Ezeket az eredményeket felhasználva az [5] cikkben azt vizsgálták, hogy egy külső energiaforrás hatására hogyan változik meg egy kristály alakja. A sematikus 2. ábrán ![]() a kék sokszög, amely a kristály egyensúlyi állapotát mutatja,
a kék sokszög, amely a kristály egyensúlyi állapotát mutatja, ![]() pedig az a pirossal jelölt alakzat, amit a hevítéssel kapunk. Figalliék megmutatták, hogy
pedig az a pirossal jelölt alakzat, amit a hevítéssel kapunk. Figalliék megmutatták, hogy ![]() egyenletesen közel van
egyenletesen közel van ![]() -hoz, sőt a közelség mértékét egy olyan konstanssal tudták kontrollálni, ami csak a tér dimenziójától,
-hoz, sőt a közelség mértékét egy olyan konstanssal tudták kontrollálni, ami csak a tér dimenziójától, ![]() felületi energiájától, és a rendszerhez hozzáadott energiától függ.
felületi energiájától, és a rendszerhez hozzáadott energiától függ.
2. Speciális metrikus terek
Röviden emlékeztetünk a metrikus tér fogalmára. Legyen ![]() egy nemüres halmaz, amelyen adott egy
egy nemüres halmaz, amelyen adott egy ![]() függvény, amely teljesíti az
függvény, amely teljesíti az
i) minden ![]() -re
-re ![]() ,
,
ii) minden ![]() -re
-re ![]() ,
,
iii) minden ![]() -re
-re ![]() .
.
feltételeket. Ekkor a ![]() függvényt metrikának, a
függvényt metrikának, a ![]() -val ellátott
-val ellátott ![]() halmazt (röviden az
halmazt (röviden az ![]() párt) metrikus térnek nevezzük. Mostantól olyan speciális metrikus terekről lesz szó, amelyeknél
párt) metrikus térnek nevezzük. Mostantól olyan speciális metrikus terekről lesz szó, amelyeknél ![]() szerepét az
szerepét az ![]() tér Borel valószínűségi mértékeinek egy-egy kitüntetett részhalmaza játssza.
tér Borel valószínűségi mértékeinek egy-egy kitüntetett részhalmaza játssza.
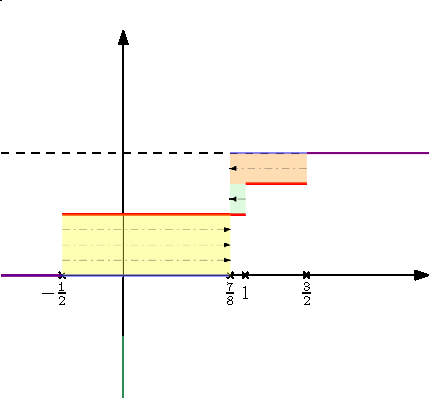
Az egyszerűség kedvéért tegyük fel most, hogy a mértékek a valós számegyenesen élnek, azaz ![]() . Ebben a speciális esetben minden
. Ebben a speciális esetben minden ![]() mérték helyett tekinthetjük az ő eloszlásfüggvényét, azaz az
mérték helyett tekinthetjük az ő eloszlásfüggvényét, azaz az
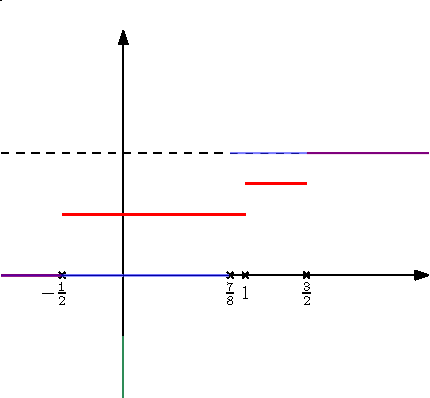
függvényt. A 3. ábrán a ![]() és a
és a ![]() mértékekhez tartozó eloszlásfüggvények láthatók. Egy eloszlásfüggvény általában nem szigorúan monoton, így a hagyományos értelemben vett inverzéről nem beszélhetünk. Ennek ellenére definiálhatunk egyfajta általánosított inverzet:
mértékekhez tartozó eloszlásfüggvények láthatók. Egy eloszlásfüggvény általában nem szigorúan monoton, így a hagyományos értelemben vett inverzéről nem beszélhetünk. Ennek ellenére definiálhatunk egyfajta általánosított inverzet:
A 4. ábrán a fenti eloszlásfüggvények általánosított inverzei láthatók.
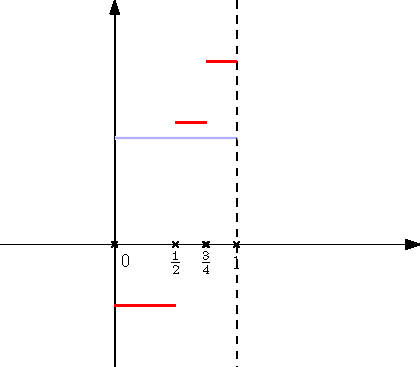
4. ábra
Ismerkedjünk meg három olyan nevezetes metrikával, amelyeket eloszlásfüggvények segítségével definiálnak.
2.1. A Kolmogorov–Smirnov távolság
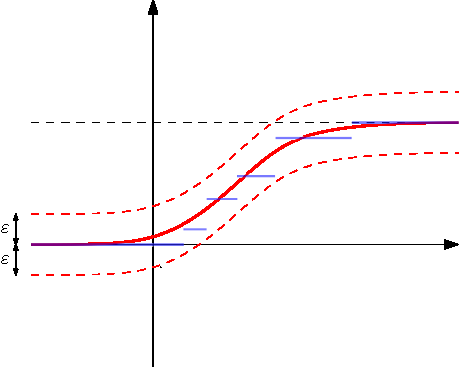
Két valószínűségi mérték Kolmogorov–Smirnov távolságát a
formulával definiáljuk. Tehát ![]() , ha
, ha ![]() az
az ![]() -re ilesztett
-re ilesztett ![]() -sávon belül halad (lásd 5. ábra). Ez a metrika ismerős lehet azoknak, akik már találkoztak a Kolmogorov-Smirnov próbával, amelyet a statisztikában illeszkedésvizsgálatra, illetve homogenitásvizsgálatra használnak.
-sávon belül halad (lásd 5. ábra). Ez a metrika ismerős lehet azoknak, akik már találkoztak a Kolmogorov-Smirnov próbával, amelyet a statisztikában illeszkedésvizsgálatra, illetve homogenitásvizsgálatra használnak.
2.2. A Lévy-távolság
Második példánk a Lévy-metrika, az egyik olyan metrika, ami a gyenge konvergenciát metrizálja. Két valószínűségi mérték Lévy-távolságát így definiáljuk:
Az alábbi 6. ábra azt szemlélteti, hogy egy ![]() érték mikor elégíti ki a definícióban látható egyenlőtlenség láncot.
érték mikor elégíti ki a definícióban látható egyenlőtlenség láncot.
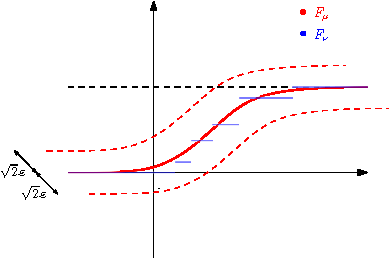
Azt látjuk, hogy ![]() -nek az
-nek az ![]() átlós irányban vett
átlós irányban vett ![]() -nal való eltoltjai között kell haladni. A két ábra első ránézésre elég hasonló, de nem szabad elfelejteni, hogy a Lévy-metrikánál a függvények változójában is történik eltolás. Ezáltal a metrika érzékeny lesz nem csak arra, hogy az
-nal való eltoltjai között kell haladni. A két ábra első ránézésre elég hasonló, de nem szabad elfelejteni, hogy a Lévy-metrikánál a függvények változójában is történik eltolás. Ezáltal a metrika érzékeny lesz nem csak arra, hogy az ![]() és
és ![]() egy adott
egy adott ![]() pontban mennyire tér el egymástól, hanem arra is, hogy a számegyenes
pontban mennyire tér el egymástól, hanem arra is, hogy a számegyenes ![]() -hez közeli pontjaiban hogyan alakulnak az eloszlások.
-hez közeli pontjaiban hogyan alakulnak az eloszlások.
Erre a tényre elég jól rávilágít, ha kiszámoljuk két Dirac-mérték távolságát. Ha ![]() két tetszőleges pont, akkor
két tetszőleges pont, akkor ![]() , míg
, míg ![]() . Azt látjuk, hogy a Kolmogorov-Smirnov metrika semmilyen információt nem ad vissza
. Azt látjuk, hogy a Kolmogorov-Smirnov metrika semmilyen információt nem ad vissza ![]() és
és ![]() távolságáról, azaz
távolságáról, azaz ![]() -ról. Ezzel szemben a Lévy-metrika segítségével ki tudjuk olvasni a tartó pontok távolságát, amennyiben az kisebb, mint 1.
-ról. Ezzel szemben a Lévy-metrika segítségével ki tudjuk olvasni a tartó pontok távolságát, amennyiben az kisebb, mint 1.
Ezen a ponton rátérhetünk a transzport tervekhez köthető metrikák tárgyalására.
2.3. A Kantorovics-távolság
A Lévy-metrikát általában kicsi mennyiségek becslésére alkalmazzák, így nem okoz gondot, hogy a metrika semmit nem tud mondani azokról a mértékekről, amelyek egymástól távol vannak. Ha olyan problémát akarunk kezelni, ahol nem csak kicsi mennyiségekkel kell dolgozni, akkor másik metrikát kell használnunk. Ahhoz hogy a következő definíció értelmes legyen, meg kell szorítanunk a valószínűségi mértékek ![]() halmazát. Vegyük azokat a valószínűségi mértékeket, amelyeknek véges a várható értéke. Ha
halmazát. Vegyük azokat a valószínűségi mértékeket, amelyeknek véges a várható értéke. Ha ![]() és
és ![]() két ilyen mérték, akkor a
két ilyen mérték, akkor a
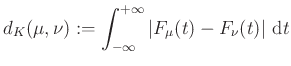
integrál véges. Azt látjuk, hogy egyrészt ![]() , másrészt azt is megsejthetjük, hogy ennek a metrikának már köze lesz a szállítási feladatokhoz.
, másrészt azt is megsejthetjük, hogy ennek a metrikának már köze lesz a szállítási feladatokhoz.
Erre később visszatérünk, sejtésünket egyelőre a 7. ábrával szemléltetjük. Tekintsük megint a 3. ábrán látható mértékeket. A definícióban szereplő integrál értéke éppen a (különböző színekkel jelölt) téglalapok összterülete. Egy-egy téglalap területe pedig nem más, mint a megfelelő súlyok mozgatásának költsége, ha ![]() egység
egység ![]() -ből
-ből ![]() -ba való mozgatásának költsége
-ba való mozgatásának költsége ![]() . Valójában amit itt látunk (a véges várható értékű mértékek halmaza a Kantorovics-metrikával ellátva) egy Wasserstein-tér. Hogy pontosan hogyan kell ezt érteni, az a következő fejezetből kiderül.
. Valójában amit itt látunk (a véges várható értékű mértékek halmaza a Kantorovics-metrikával ellátva) egy Wasserstein-tér. Hogy pontosan hogyan kell ezt érteni, az a következő fejezetből kiderül.
3. A 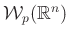 Wasserstein-tér
Wasserstein-tér
Rátérünk a Wasserstein-tér definíciójára. Legyen ![]() egy rögzített szám. Jelölje
egy rögzített szám. Jelölje ![]() a véges
a véges ![]() -edik momentumú valószínűségi mértékek halmazát
-edik momentumú valószínűségi mértékek halmazát
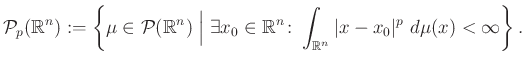
Ez a mértékcsalád szolgáltatja a ![]() -Wasserstein-tér alaphalmazát. Noha nem egészen magától értetődő, be lehet bizonyítani, hogy a
-Wasserstein-tér alaphalmazát. Noha nem egészen magától értetődő, be lehet bizonyítani, hogy a
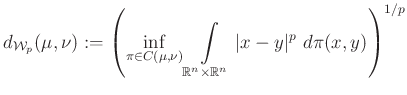
kétváltozós függvény metrika a ![]() halmazon. A
halmazon. A ![]() függvényt
függvényt ![]() -Wassertein-távolságnak, a
-Wassertein-távolságnak, a ![]() párt az
párt az ![]() feletti
feletti ![]() -Wasserstein-térnek nevezzük és röviden
-Wasserstein-térnek nevezzük és röviden ![]() -nel jelöljük.
-nel jelöljük.
Világos a kapcsolat a metrika és a transzport probléma között: két mérték távolsága nem más, mint az optimális transzport költsége a ![]() költségfüggvény mellett. Megjegyezzük, hogy Wasserstein-teret bármilyen szeparábilis metrikus térre lehet építeni. Azaz ha
költségfüggvény mellett. Megjegyezzük, hogy Wasserstein-teret bármilyen szeparábilis metrikus térre lehet építeni. Azaz ha ![]() egy ilyen tér, akkor
egy ilyen tér, akkor ![]() helyére
helyére ![]() -et,
-et, ![]() helyére
helyére ![]() -t írva és a transzport terv fogalmát értelemszerűen módosítva a
-t írva és a transzport terv fogalmát értelemszerűen módosítva a ![]() Wasserstein-tér definícióját kapjuk.
Wasserstein-tér definícióját kapjuk.
Könnyű meggondolni, hogy ha ![]() és
és ![]() közül legalább az egyik egy Dirac-mérték, akkor
közül legalább az egyik egy Dirac-mérték, akkor ![]() halmaz egyetlen eleme a szorzatmérték, és így a távolság könnyen kiszámítható. Egy ilyen egyszerű számítás mutatja, hogy a Wasserstein-távolságból ki lehet olvasni az alul fekvő tér metrikáját:
halmaz egyetlen eleme a szorzatmérték, és így a távolság könnyen kiszámítható. Egy ilyen egyszerű számítás mutatja, hogy a Wasserstein-távolságból ki lehet olvasni az alul fekvő tér metrikáját:
Azt is mondhatnánk, hogy a Wasserstein-tér alján Dirac-mértékek formájában ott ül az ![]() -nek egy másolata. Ezek a Dirac-mértékek a térnek egyfajta építőkövei abban az értelemben, hogy tetszőleges
-nek egy másolata. Ezek a Dirac-mértékek a térnek egyfajta építőkövei abban az értelemben, hogy tetszőleges ![]() -hez és
-hez és ![]() -hoz van olyan
-hoz van olyan ![]() mérték, amelyre
mérték, amelyre ![]() .
.
Felmerülhet a kérdés, hogy különböző ![]() értékekre a
értékekre a ![]() terek mennyire térnek el egymástól. Az egyszerűség kedvéért ismét az
terek mennyire térnek el egymástól. Az egyszerűség kedvéért ismét az ![]() esetet, tehát a számegyenes esetét fogjuk vizsgálni. A
esetet, tehát a számegyenes esetét fogjuk vizsgálni. A ![]() -Wasserstein-metrika
-Wasserstein-metrika
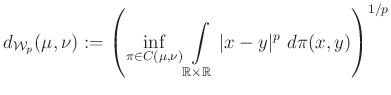
definícióját látva az embernek az a benyomása támad, hogy amit lát, az az ![]() függvénytér mértékelméleti analogonja. Ebben az esetben egy egyszerű analógiánál többről van szó: a
függvénytér mértékelméleti analogonja. Ebben az esetben egy egyszerű analógiánál többről van szó: a ![]() Wasserstein-tér beágyazható az
Wasserstein-tér beágyazható az ![]() térbe az általánosított inverzek segítségével. Nevezetesen, minden
térbe az általánosított inverzek segítségével. Nevezetesen, minden ![]() -re
-re
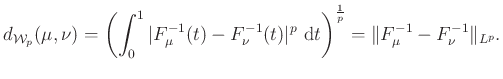
Ha egy pillanatra visszagondolunk az 7. ábrára és a Kantorovics-metrikára, akkor egy egyszerű integrál átalakítással megállapíthatjuk, hogy ott éppen az ![]() -Wasserstein-távolságot láttuk.
-Wasserstein-távolságot láttuk.
A fenti ![]() beágyazásnak a létezéséből már sejthető, hogy különböző
beágyazásnak a létezéséből már sejthető, hogy különböző ![]() értékekre a
értékekre a ![]() terek szerkezete eltérő, és hogy a
terek szerkezete eltérő, és hogy a ![]() és a
és a ![]() esetek különlegesek. A
esetek különlegesek. A ![]() azért, mert az
azért, mert az ![]()
![]() terek közül az
terek közül az ![]() az egyetlen, aminek a normája nem szigorúan konvex, a
az egyetlen, aminek a normája nem szigorúan konvex, a ![]() pedig azért, mert az
pedig azért, mert az ![]() terek között az
terek között az ![]() az egyetlen Hilbert tér.
az egyetlen Hilbert tér.
A ![]() tér gazdagságát jól mutatja, hogy a többi
tér gazdagságát jól mutatja, hogy a többi ![]() térrel összehasonlítva sokkal több szimmetriája van. Szimmetria alatt olyan bijektív
térrel összehasonlítva sokkal több szimmetriája van. Szimmetria alatt olyan bijektív ![]() leképezéseket értünk, amelyek megtartják a távolságot, azaz
leképezéseket értünk, amelyek megtartják a távolságot, azaz
Be lehet bizonyítani, hogy a ![]() tér szimmetriái a
tér szimmetriái a ![]() esetben éppen a számegyenes szimmetriáinak feleltethetők meg (lásd [7]). Azaz
esetben éppen a számegyenes szimmetriáinak feleltethetők meg (lásd [7]). Azaz ![]() pontosan akkor szimmetriája
pontosan akkor szimmetriája ![]() -nek, ha ő az
-nek, ha ő az ![]() egy
egy ![]() szimmetriájának az előretoltja
szimmetriájának az előretoltja
Egy véges tartójú mértéken könnyű is szemléltetni a ![]() hatását, mindössze a tartópontokat kell mozgatni:
hatását, mindössze a tartópontokat kell mozgatni:

Azt jól tudjuk, hogy mik a számegyenes szimmetriái: eltolások és csúsztatva tükrözések. Innen könnyű meggondolni, hogy ha ![]() a
a ![]() -nek
-nek ![]() egy olyan szimmetriája, ami két Dirac-mértéket helyben hagy, akkor minden mértéket helyben hagy. Tehát a tér meglehetősen merev. Ezzel szemben Kloeckner bebizonyította (lásd [9]), hogy a
egy olyan szimmetriája, ami két Dirac-mértéket helyben hagy, akkor minden mértéket helyben hagy. Tehát a tér meglehetősen merev. Ezzel szemben Kloeckner bebizonyította (lásd [9]), hogy a ![]() térnek van egy egész sereg olyan egzotikus szimmetriája, ami minden Dirac-mértéket fixen hagy, de mégsem igaz, hogy
térnek van egy egész sereg olyan egzotikus szimmetriája, ami minden Dirac-mértéket fixen hagy, de mégsem igaz, hogy ![]() minden
minden ![]() -re. Általában is igaz, hogy a
-re. Általában is igaz, hogy a ![]() -Wasserstein-terek struktúrája sokkal gazdagabb, emiatt az alkalmazásokban legtöbbször ezekkel a terekkel találkozhatunk.
-Wasserstein-terek struktúrája sokkal gazdagabb, emiatt az alkalmazásokban legtöbbször ezekkel a terekkel találkozhatunk.
4. Wasserstein stílustranszfer
Az optimális transzport, illetve a hozzá kötődő metrikák így például a Wasserstein-metrika nagy előnye, hogy nem csak egy számértéket rendelnek a mértékpárokhoz, de arra vonatkozóan is szolgálnak információval, hogy hogyan transzformálható át egyik mérték a másikba. A ![]() esetben ez könnyen látható: az eloszlásfüggvények általánosított inverzeit kell egymásba mozgatni, ahogy az a 8. ábrán látható.
esetben ez könnyen látható: az eloszlásfüggvények általánosított inverzeit kell egymásba mozgatni, ahogy az a 8. ábrán látható.

De nem csak a valós számok, vagy ![]() esetén ennyire szép a helyzet. Általánosabban, ha
esetén ennyire szép a helyzet. Általánosabban, ha ![]() egy Riemann-sokaság, akkor a
egy Riemann-sokaság, akkor a ![]() tér nagyon jó geometriai tulajdonságokkal rendelkezik. Emiatt a transzportelméletnek rengeteg alkalmazása van nem csak az elméleti matematikában, hanem az alkalmazott tudományokban is. Így például a jel- és képfeldolgozásban [10], [14], az alakfelismerésben [8], a szín és textúra modellezésben [3], [15], vagy a gépi tanulásban [2], [6]. A cikket egy képmanipuláló eljárás vázlatos bemutatásával zárjuk. A feladat a következő: adott két kép,
tér nagyon jó geometriai tulajdonságokkal rendelkezik. Emiatt a transzportelméletnek rengeteg alkalmazása van nem csak az elméleti matematikában, hanem az alkalmazott tudományokban is. Így például a jel- és képfeldolgozásban [10], [14], az alakfelismerésben [8], a szín és textúra modellezésben [3], [15], vagy a gépi tanulásban [2], [6]. A cikket egy képmanipuláló eljárás vázlatos bemutatásával zárjuk. A feladat a következő: adott két kép, ![]() és
és ![]() .
.


B. ábra
Az ![]() képet akarjuk manipulálni úgy, hogy az eredmény rendelkezzen a
képet akarjuk manipulálni úgy, hogy az eredmény rendelkezzen a ![]() stílusjegyeivel.
stílusjegyeivel.

A feladatot egy konvolúciós neurális háló végzi el: beazonosítja a két kép jellegzetességeit, és átkódolja őket egy-egy valószínűségi mértékké. Jelölje ezeket a mértékeket ![]() . Innentől kezdve a
. Innentől kezdve a ![]() Wasserstein-téren dolgozunk: egy olyan
Wasserstein-téren dolgozunk: egy olyan ![]() mértéket keresünk, amit ha visszakódolunk, akkor olyan képet kapunk, ami rendelkezik a kívánt tulajdonsággal. Sőt, nem is elégszünk meg ennyivel, a stilizálás erősségét is be akarjuk állítani.
mértéket keresünk, amit ha visszakódolunk, akkor olyan képet kapunk, ami rendelkezik a kívánt tulajdonsággal. Sőt, nem is elégszünk meg ennyivel, a stilizálás erősségét is be akarjuk állítani.
Vegyük szemügyre a következő kifejezést rögzített ![]() mellett:
mellett:
Az összeg első tagja arról ad információt, hogy ha ![]() -t kódoljuk vissza, akkor mennyit vesztünk
-t kódoljuk vissza, akkor mennyit vesztünk ![]() -ból, a második tag pedig arról, hogy mennyit vesztünk
-ból, a második tag pedig arról, hogy mennyit vesztünk ![]() -ből. Látjuk, hogy ha
-ből. Látjuk, hogy ha ![]() közel van
közel van ![]() -hez, akkor a stilizálás nagyon erős, hiszen a kifejezés értékébe az első tag alig szól bele. Ha pedig
-hez, akkor a stilizálás nagyon erős, hiszen a kifejezés értékébe az első tag alig szól bele. Ha pedig ![]() kicsi, akkor a stilizálás gyenge. A
kicsi, akkor a stilizálás gyenge. A ![]() kívánt értékre való beállítása után a fenti kifejezés csak a
kívánt értékre való beállítása után a fenti kifejezés csak a ![]() -nek függvénye, a feladat az, hogy minimalizáljuk a veszteségek összegét. Ez a feladat megoldható, sőt egyetlen megoldása van, jelölje ezt
-nek függvénye, a feladat az, hogy minimalizáljuk a veszteségek összegét. Ez a feladat megoldható, sőt egyetlen megoldása van, jelölje ezt ![]() . Ezt a
. Ezt a ![]() mértéket dekódolva a kívánt erősséggel stilizált képet kapjuk. Világos, hogy
mértéket dekódolva a kívánt erősséggel stilizált képet kapjuk. Világos, hogy ![]() és
és ![]() . Az már kevésbé világos, de igaz, hogy a minimalizáló mértékek által alkotott
. Az már kevésbé világos, de igaz, hogy a minimalizáló mértékek által alkotott ![]() sereg egy
sereg egy ![]() -t
-t ![]() -vel összekötő geodetikus görbét határoz meg. Két mérték ilyen módon való összekötését McCann-interpolációnak nevezik.
-vel összekötő geodetikus görbét határoz meg. Két mérték ilyen módon való összekötését McCann-interpolációnak nevezik.
Végül megjegyezzük, hogy a transzfer bemutatásánál két nehézséget is átugrottunk: az első, hogy hogyan kódolja és dekódolja a neurális háló a képeket/mértékeket. A másik probléma, hogy technikailag hogyan oldja meg az ember a minimalizálási feladatot, vagy általában, hogyan lehet hatékonyan kiszámolni a ![]() -Wasserstein-távolságot. Erről az olvasó többet is megtudhat a [13] cikkben.
-Wasserstein-távolságot. Erről az olvasó többet is megtudhat a [13] cikkben.
A cikk az ITM és az NKFIH ÚNKP-19-4-BGE-1 és PD128374 kódszámú projektjeinek, valamint az MTA Bolyai János Kutatási Ösztöndíjának támogatásával készült.
Irodalomjegyzék
- [1] Y. Brenier, Polar factorization and monotone rearrangement of vector-valued functions, Commun. Pure Appl. Math. 44(4) (1991), 375–417.
- [2] N. Courty, R. Flamary, D. Tuia, Domain adaptation with regularized optimal transport, Machine Learning and Knowledge Discovery in Databases, Springer, 274–289.
- [3] S. Ferradans, G.S. Xia, G. Peyré, J.F. Aujol, Static and dynamic texture mixing using optimal transport, Springer; 2013.
- [4] A. Figalli, F. Maggi, A. Pratelli, A mass transportation approach to quantitative isoperimetric inequalities, Invent. Math. 182 (2010), no. 1, 167–211.
- [5] A. Figalli, F. Maggi, On the shape of liquid drops and crystals in the small mass regime, Arch. Ration. Mech. Anal. 201 (2011), no. 1, 143–207.
- [6] C. Frogner, C. Zhang, H. Mobahi, M. Araya, T. A. Poggio, Learning with a Wasserstein loss, Advances in Neural Information Processing Systems, 2015:2044–2052.
- [7] Gy. P. Gehér, T. Titkos, D. Virosztek, Isometric study of Wasserstein spaces – The real line, Trans. Amer. Math. Soc., Volume 373, Number 8, August 2020, Pages 5855--5883.
- [8] S. Haker, L. Zhu, A. Tannenbaum, S. Angenent, Optimal mass transport for registration and warping. International Journal of Computer Vision. 2004;60(3):225–240.
- [9] B. Kloeckner, A geometric study of Wasserstein spaces: Euclidean spaces, Annali della Scuola Normale Superiore di Pisa - Classe di Scienze IX, 2 (2010), 297–323.
- [10] S. Kolouri, A.B. Tosun, J.A. Ozolek, G.K. Rohde, A continuous linear optimal transport approach for pattern analysis in image datasets. Pattern Recognition. 2016;51:453–462.
- [11] R.J. McCann, Existence and uniqueness of monotone measure-preserving maps, Duke Math. J., 80 (2) (1995), 309–323.
- [12] R. J. McCann, A convexity principle for interacting gases, Adv. Math. 128 (1) (1997), 153–179.
- [13] Y. Mroueh, Wasserstein Style Transfer, arxiv:1905.12828
- [14] S. R. Park, S. Kolouri, S. Kundu, G.K. Rohde GK, The cumulative distribution transform and linear pattern classification, Applied and Computational Harmonic Analysis. 2017.
- [15] J. Rabin, S. Ferradans, N. Papadakis, Adaptive color transfer with relaxed optimal transport, Image Processing (ICIP), IEEE 2014.; pp. 4852–4856.
- [16] G. Wulff, Zur Frage der Geschwindigkeit des Wachstums und der Auflösung der Krystallflagen, Zeitschrift für Krystallographie und Mineralogie. 34 (5/6) (1901) 449–530.









