Napjainkban sok szó esik arról, hogy hány tesztet kellene elvégezni ahhoz, hogy kellő pontossággal ismerni lehessen a fertőzöttek vagy fertőzésen átesettek számát egy bizonyos betegség esetén. Ez számos matematikai kérdést felvet. Ebben az írásban arról szólunk, hogy ideális feltételek mellett a fertőzésen átesettek országos arányát hány teszt elvégzésével lehet biztonságosan megállapítani.
Egyszerű számpéldával a következőképpen lehet a kérdést megvilágítani. Tegyük fel, hogy a társadalom ![]() -a esett át a fertőzésen, de ennek kiderítéséhez természetesen nem szeretnénk 10 millió emberen a tesztet elvégezni, csak kisebb mintán. Például, ha 100 embertől veszünk mintát, akkor, ha szerencsénk van, éppen 10 fertőzésen átesett egyént találunk, ami éppen az országos átlagot adná, de könnyen lehet, hogy 100-ból 8-at vagy 11-et kapunk, és tévesen becsüljük meg a valódi arányt. Ekkor tesztelhetünk újabb száz embert, majd ismét újabbat. A kérdés az, hogy hányszor kell ezt elvégezni, és milyen biztonsággal tudjuk a példa elején említett 10 százalékot megkapni. Ezt a bevezető valószínűségszámítás kurzusokon (közgazdasági, mérnöki szakokon is) elsajátított matematikai eszköztár segítségével magunk is kiszámolhatjuk, ezért örömmel osztjuk meg az Olvasóval ennek egy lehetséges módszerét. A végeredményt még nem áruljuk el, a kíváncsiak előrelapozhatnak és megleshetik. Aki pedig sorban haladva olvassa a cikket, azt elkalauzoljuk olyan témákhoz, mint a Stirling-formula, Gauss-görbe és centrális határeloszlás-tétel, sőt még az is kiderül, hogy nem volt felesleges megismerni analízisből az integrálközelítő összeg fogalmát és megtanulni a helyettesítéses integrálást.
-a esett át a fertőzésen, de ennek kiderítéséhez természetesen nem szeretnénk 10 millió emberen a tesztet elvégezni, csak kisebb mintán. Például, ha 100 embertől veszünk mintát, akkor, ha szerencsénk van, éppen 10 fertőzésen átesett egyént találunk, ami éppen az országos átlagot adná, de könnyen lehet, hogy 100-ból 8-at vagy 11-et kapunk, és tévesen becsüljük meg a valódi arányt. Ekkor tesztelhetünk újabb száz embert, majd ismét újabbat. A kérdés az, hogy hányszor kell ezt elvégezni, és milyen biztonsággal tudjuk a példa elején említett 10 százalékot megkapni. Ezt a bevezető valószínűségszámítás kurzusokon (közgazdasági, mérnöki szakokon is) elsajátított matematikai eszköztár segítségével magunk is kiszámolhatjuk, ezért örömmel osztjuk meg az Olvasóval ennek egy lehetséges módszerét. A végeredményt még nem áruljuk el, a kíváncsiak előrelapozhatnak és megleshetik. Aki pedig sorban haladva olvassa a cikket, azt elkalauzoljuk olyan témákhoz, mint a Stirling-formula, Gauss-görbe és centrális határeloszlás-tétel, sőt még az is kiderül, hogy nem volt felesleges megismerni analízisből az integrálközelítő összeg fogalmát és megtanulni a helyettesítéses integrálást.
1. A mintavételezés modellje: a binomális eloszlás
Induljon hát a matematikaóra. Ahhoz, hogy egy adott pontossághoz és bizonyossághoz tartozó szükséges tesztek számát meghatározzuk, először azt a kérdést értjük meg alaposabban, hogy adott számú teszt és ismert védettségi arány esetén mennyi a valószínűsége, hogy például legfeljebb ![]() -ot téved a becslésünk az igazi érték arányában. A számolások során azt feltételezzük, hogy a tesztek egymástól függetlenek, és tökéletes megbízhatósággal mutatják ki a fertőzést, nincs tévedés egyik irányban sem. A kérdés az egyszerű pénzfeldobáshoz (Bernoulli trials) hasonló, az egyének
-ot téved a becslésünk az igazi érték arányában. A számolások során azt feltételezzük, hogy a tesztek egymástól függetlenek, és tökéletes megbízhatósággal mutatják ki a fertőzést, nincs tévedés egyik irányban sem. A kérdés az egyszerű pénzfeldobáshoz (Bernoulli trials) hasonló, az egyének ![]() valószínűséggel átestek a fertőzésen, őket védetteknek fogjuk nevezni,
valószínűséggel átestek a fertőzésen, őket védetteknek fogjuk nevezni, ![]() valószínűséggel pedig nem. Ennek a
valószínűséggel pedig nem. Ennek a ![]() -nek az értékre leszünk kíváncsiak adott pontossággal. Legyen
-nek az értékre leszünk kíváncsiak adott pontossággal. Legyen ![]() azon emberek száma
azon emberek száma ![]() vizsgált személy közül, akiknél kimutatta a teszt a védettséget. Ennek értéke véletlen, azaz
vizsgált személy közül, akiknél kimutatta a teszt a védettséget. Ennek értéke véletlen, azaz ![]() egy valószínűségi változó. Ekkor a
egy valószínűségi változó. Ekkor a ![]() -t becsülni az
-t becsülni az ![]() -nel, vagyis a védettek relatív gyakoriságával tudjuk a legegyszerűbben és sok szempontból a legjobban (egy ezzel kapcsolatos kérdésre a cikk második részében fogunk kitérni). A becslésre azt a feltételt fogalmaztuk meg, hogy a relatív hibája legfeljebb
-nel, vagyis a védettek relatív gyakoriságával tudjuk a legegyszerűbben és sok szempontból a legjobban (egy ezzel kapcsolatos kérdésre a cikk második részében fogunk kitérni). A becslésre azt a feltételt fogalmaztuk meg, hogy a relatív hibája legfeljebb ![]() legyen:
legyen:
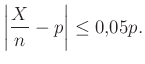 |
(1) |
Mivel a védettek száma, azaz ![]() értéke 0 és
értéke 0 és ![]() között tetszőleges lehet, olyan feltételt nem fogunk tudni mondani, amire ez biztosan teljesül, bárhogyan is alakul a mintavételezés. Azt azonban már kitűzhetjük célnak, hogy ez minél nagyobb, például legalább
között tetszőleges lehet, olyan feltételt nem fogunk tudni mondani, amire ez biztosan teljesül, bárhogyan is alakul a mintavételezés. Azt azonban már kitűzhetjük célnak, hogy ez minél nagyobb, például legalább ![]() valószínűséggel teljesüljön.
valószínűséggel teljesüljön.
Ehhez pedig először a fenti esemény valószínűségét szeretnénk tehát kiszámítani. Ha ![]() egyént tesztelünk, akkor a középiskolában tanult képlet alapján annak valószínűsége, hogy
egyént tesztelünk, akkor a középiskolában tanult képlet alapján annak valószínűsége, hogy ![]() védettet találunk:
védettet találunk:
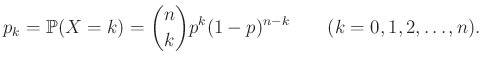 |
(2) |
Ez a jól ismert binomiális eloszlás, ami azt is megadja, hogy ha egy urnában a golyók ![]() -ed része piros, akkor mennyi annak valószínűsége, hogy
-ed része piros, akkor mennyi annak valószínűsége, hogy ![]() -szer visszatevéssel húzva pontosan
-szer visszatevéssel húzva pontosan ![]() pirosat kapunk.
pirosat kapunk.
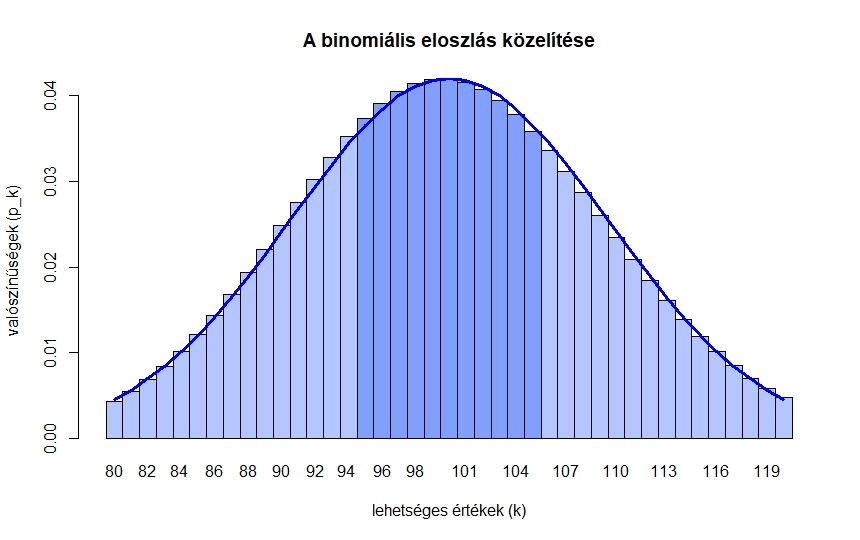
1. ábra. A binomiális eloszlás ![]() renddel és
renddel és ![]() paraméterrel, valamint a közelítő függvény (4) alapján
paraméterrel, valamint a közelítő függvény (4) alapján
Már az egyetemi bevezető matematika órára átlépve, tanultuk, hogy ennek várható értéke ![]() , azaz átlagosan ennyi védettet fogunk találni az
, azaz átlagosan ennyi védettet fogunk találni az ![]() tesztelt egyén között. Ha például
tesztelt egyén között. Ha például ![]() tesztelést végzünk, és az emberek 10 százaléka védett, azaz
tesztelést végzünk, és az emberek 10 százaléka védett, azaz ![]() , akkor várhatóan 100 védettet fogunk találni. Valójában persze lehet, hogy 95-öt vagy 110-et. Ha 95 védettet találunk, akkor a becslésünk
, akkor várhatóan 100 védettet fogunk találni. Valójában persze lehet, hogy 95-öt vagy 110-et. Ha 95 védettet találunk, akkor a becslésünk ![]() lesz, ezzel az igazi
lesz, ezzel az igazi ![]() -hez viszonyítva legfeljebb
-hez viszonyítva legfeljebb ![]() -t tévedtünk, azaz az
-t tévedtünk, azaz az ![]() relatív hibahatáron belül maradunk. Ha viszont
relatív hibahatáron belül maradunk. Ha viszont ![]() , akkor a becslésünk 0,11, ez már
, akkor a becslésünk 0,11, ez már ![]() -os hibát jelentene. Vagyis az (1) egyenlet alapján annak a valószínűségét szeretnénk kiszámítani, hogy a
-os hibát jelentene. Vagyis az (1) egyenlet alapján annak a valószínűségét szeretnénk kiszámítani, hogy a ![]() -től
-től ![]() -ig terjedő intervallumba esik a védettek száma. A (2) képletből ez a valószínűség egyszerűen a
-ig terjedő intervallumba esik a védettek száma. A (2) képletből ez a valószínűség egyszerűen a
összeg. Az 1. ábrán láthatjuk a binomiális eloszlást ![]() -tól
-tól ![]() -ig,
-ig, ![]() és
és ![]() esetén. Az oszlopok szélessége
esetén. Az oszlopok szélessége ![]() , a magasságokat a fenti
, a magasságokat a fenti ![]() -k adják meg, így a sötétebb rész területét kell meghatároznunk.
-k adják meg, így a sötétebb rész területét kell meghatároznunk.
Az alábbi octave kód abban lesz segítségünkre, hogy ezt numerikusan kiszámítsuk. Más programokban, például Matlabban vagy R-ben is egy hasonlóképpen megírt algoritmust használhatnánk, illetve ezen programoknak a binomiális eloszlásra vonatkozó beépített függvényeit is (például binocdf(105, 1000, 0.1)-binocdf(94, 1000, 0.1) az octave-ban). Ez a hosszabb kód viszont a számítás menetét is illusztrálja. Az mv vektor azokat a lehetséges értékeket tartalmazza, melyek a megengedett tartományba esnek. A pk függvény adott ![]() számok és
számok és ![]() , pozitív egészekből álló vektor esetén egy olyan vektort ad vissza, aminek a
, pozitív egészekből álló vektor esetén egy olyan vektort ad vissza, aminek a ![]() eleme éppen a fent definiált
eleme éppen a fent definiált ![]() . A logaritmusra való áttérés oka, hogy nagy
. A logaritmusra való áttérés oka, hogy nagy ![]() esetén a binomiális együttható értéke is nagyon nagy,
esetén a binomiális együttható értéke is nagyon nagy, ![]() pedig nagyon kicsi lehet, és a szorzásnál megbízhatóbb a logaritmusok kiszámítása és összeadása, így kisebb a számítógép kerekítéseiből adódó hiba. Végül a keresett tartományba eső valószínűségeknek, azaz binmv elemeinek az összege adja meg a kérdéses valószínűséget.
pedig nagyon kicsi lehet, és a szorzásnál megbízhatóbb a logaritmusok kiszámítása és összeadása, így kisebb a számítógép kerekítéseiből adódó hiba. Végül a keresett tartományba eső valószínűségeknek, azaz binmv elemeinek az összege adja meg a kérdéses valószínűséget.
n=1000; p=0.1; hiba=0.05;
mv=[round(n*p*(1-hiba)): round(n*p*(1+hiba))];
binmv=bineloszl(n,p,mv);
function pk=bineloszl(n,p,k)
bnc=[];
for j=1:length(k)
mj=m(j);
bnc=[bnc bincoeff(n,mk)];
end
lpk=log(bnc)+k*log(p)+(n-k)*log(1-p);
pk=exp(lpk);
endfunction
sum(binmv)
Ebből azt kapjuk, hogy ![]() és
és ![]() esetén annak valószínűsége, hogy a becslésünk relatív hibája legfeljebb
esetén annak valószínűsége, hogy a becslésünk relatív hibája legfeljebb ![]() , vagyis az (1) képletben felírt esemény valószínűsége:
, vagyis az (1) képletben felírt esemény valószínűsége:
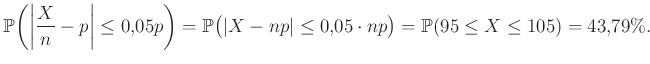 |
(3) |
2. A binomiális eloszlás tagjainak közelítése a haranggörbével
Ezzel tehát adott mintaelemszám esetén már tudunk számolni. Ugyanakkor az imént kapott érték azt jelenti, hogy több mint ![]() valószínűséggel tévedünk a megengedett
valószínűséggel tévedünk a megengedett ![]() relatív hibánál többet. Ennél jobb eredményt szeretnénk elérni, vagyis több mint ezer tesztre van szükség. A fenti közvetlen számolásból azonban nem látszik, hogy pontosan hány darabra, ráadásul nagyobb
relatív hibánál többet. Ennél jobb eredményt szeretnénk elérni, vagyis több mint ezer tesztre van szükség. A fenti közvetlen számolásból azonban nem látszik, hogy pontosan hány darabra, ráadásul nagyobb ![]() esetén a közelítésekből túlságosan sok hiba adódhat (például ha
esetén a közelítésekből túlságosan sok hiba adódhat (például ha ![]() és
és ![]() , akkor a binomiális együttható már
, akkor a binomiális együttható már ![]() -jegyű, ha
-jegyű, ha ![]() , akkor több mint
, akkor több mint ![]() számjegyből áll). Ennél egyszerűbben és megbízhatóbban számolhatunk, ha a fenti módszer helyett, ahogy az 1. ábra is sugallja, a kapott valószínűséget egy integrálközelítő összegnek tekintjük.
számjegyből áll). Ennél egyszerűbben és megbízhatóbban számolhatunk, ha a fenti módszer helyett, ahogy az 1. ábra is sugallja, a kapott valószínűséget egy integrálközelítő összegnek tekintjük.
Így ahhoz a kérdéshez jutunk, hogy mi is az a függvény, amit ezek a ![]() valószínűségek közelítenek. Mivel a binomiális együtthatókban faktoriálisok szerepelnek, a közelítésre az ezek aszimptotikus viselkedését leíró Stirling-formula ad lehetőséget:
valószínűségek közelítenek. Mivel a binomiális együtthatókban faktoriálisok szerepelnek, a közelítésre az ezek aszimptotikus viselkedését leíró Stirling-formula ad lehetőséget:
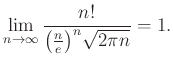
Innen elindulva számos további lépésen keresztül juthatunk el a de Moivre–Laplace-tétel lokális alakjáig, mely szerint
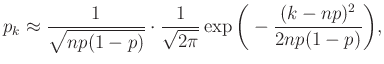 |
(4) |
ha a ![]() távolság nem több
távolság nem több ![]() -nál,
-nál, ![]() megfelelően nagy, illetve
megfelelően nagy, illetve ![]() és
és ![]() közül egyik sem túlságosan kicsi. A tétel ennél valójában sokkal erősebbet is állít, és pontosabban is megfogalmazható [4], [8]. Hasonló állítást de Moivre már 1730-ban publikált a
közül egyik sem túlságosan kicsi. A tétel ennél valójában sokkal erősebbet is állít, és pontosabban is megfogalmazható [4], [8]. Hasonló állítást de Moivre már 1730-ban publikált a ![]() esetben [7], Laplace pedig ezt általánosította a XIX. század első felében más
esetben [7], Laplace pedig ezt általánosította a XIX. század első felében más ![]() értékekre [6]. Ezzel tehát kapunk egy képletet az 1. ábrán látható tengelyesen szimmetrikus közelítő függvényre. Az ehhez hasonló (ebből eltolással vagy nyújtással megkapható) függvényeket szokták haranggörbének vagy Gauss-görbének nevezni.
értékekre [6]. Ezzel tehát kapunk egy képletet az 1. ábrán látható tengelyesen szimmetrikus közelítő függvényre. Az ehhez hasonló (ebből eltolással vagy nyújtással megkapható) függvényeket szokták haranggörbének vagy Gauss-görbének nevezni.
Az alábbi octave kód azt számolja, hogy mit kapunk a ![]() valószínűségre, ha az előző esethez hasonlóan először meghatározzuk a megfelelő értékek halmazát, mindegyikre kiszámítjuk a
valószínűségre, ha az előző esethez hasonlóan először meghatározzuk a megfelelő értékek halmazát, mindegyikre kiszámítjuk a ![]() -nak a most megadott közelítését, majd ezeket összeadjuk.
-nak a most megadott közelítését, majd ezeket összeadjuk.
n=10000; p=0.1; hiba=0.05;
mv=[round(n*p*(1-hiba)): round(n*p*(1+hiba))];
function pkkoz=bineloszlnormkoz(n,p,kv)
kvu=-1*(kv-n*p).![]() 2/(2*n*p*(1-p));
2/(2*n*p*(1-p));
pkkoz=exp(kvu)/(sqrt(pi*2*n*p*(1-p)));
endfunction
binkoz=bineloszlnormkoz(n,p,mv);
sum(binkoz)
A számolást elvégezve az eredmény ![]() lesz. A (3) egyenlettel összehasonlítva láthatjuk, hogy ez valóban jó közelítést ad a kérdéses valószínűségre.
lesz. A (3) egyenlettel összehasonlítva láthatjuk, hogy ez valóban jó közelítést ad a kérdéses valószínűségre.
3. Összegzés helyett integrálás
Az 1. ábra alapján az volt a célunk, hogy a sötétebb rész területét, azaz a ![]() valószínűséget a haranggörbe alatti területtel közelítsük. Pontosabban, a (4) egyenlet alapján (figyelve arra, hogy az integrálás is egy
valószínűséget a haranggörbe alatti területtel közelítsük. Pontosabban, a (4) egyenlet alapján (figyelve arra, hogy az integrálás is egy ![]() hosszú intervallumon történjen):
hosszú intervallumon történjen):
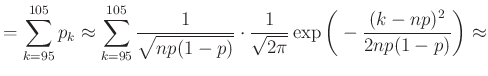 |
|
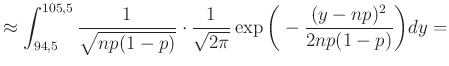 |
|
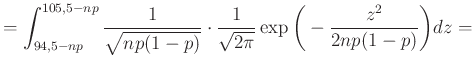 |
|
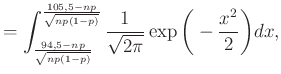 |
ahol a ![]() , majd az
, majd az ![]() változócseréket hajtottuk végre, hogy a függvény mindig ugyanaz legyen, csak a határok függjenek a változó paraméterektől.
változócseréket hajtottuk végre, hogy a függvény mindig ugyanaz legyen, csak a határok függjenek a változó paraméterektől.
A következő lépés az lehetne, hogy az integrálra explicit képletet adjunk az ![]() primitív függvényének segítségével. Ilyen azonban sajnos nincs, be is lehet bizonyítani, hogy az alapvető műveletek segítségével felírható függvények között nem találhatunk megfelelőt. Ezért az alábbi szokásos jelölést vezetjük be arra, hogy mennyi az integrál
primitív függvényének segítségével. Ilyen azonban sajnos nincs, be is lehet bizonyítani, hogy az alapvető műveletek segítségével felírható függvények között nem találhatunk megfelelőt. Ezért az alábbi szokásos jelölést vezetjük be arra, hogy mennyi az integrál ![]() -ig:
-ig:
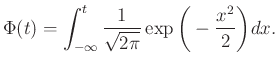
Ennek a függvénynek, amit a standard normális eloszlás eloszlásfüggvényének neveznek (erre még később visszatérünk), a ![]() helyen felvett értéke a 2. ábrán a
helyen felvett értéke a 2. ábrán a ![]() -től balra eső terület nagysága. Így például az is leolvasható, hogy
-től balra eső terület nagysága. Így például az is leolvasható, hogy ![]() . A teljes görbe alatti terület pedig
. A teljes görbe alatti terület pedig ![]() (azt, hogy
(azt, hogy ![]() esetén
esetén ![]() az integrál, polárkoordinátákra való áttéréssel lehet bizonyítani például, de ezt most nem tesszük meg, erről bővebben például itt lehet olvasni: [7.3. szakasz, 3], a normális eloszlásról pedig a [2] szimulációkat tartalmazó jegyzetben is).
az integrál, polárkoordinátákra való áttéréssel lehet bizonyítani például, de ezt most nem tesszük meg, erről bővebben például itt lehet olvasni: [7.3. szakasz, 3], a normális eloszlásról pedig a [2] szimulációkat tartalmazó jegyzetben is).
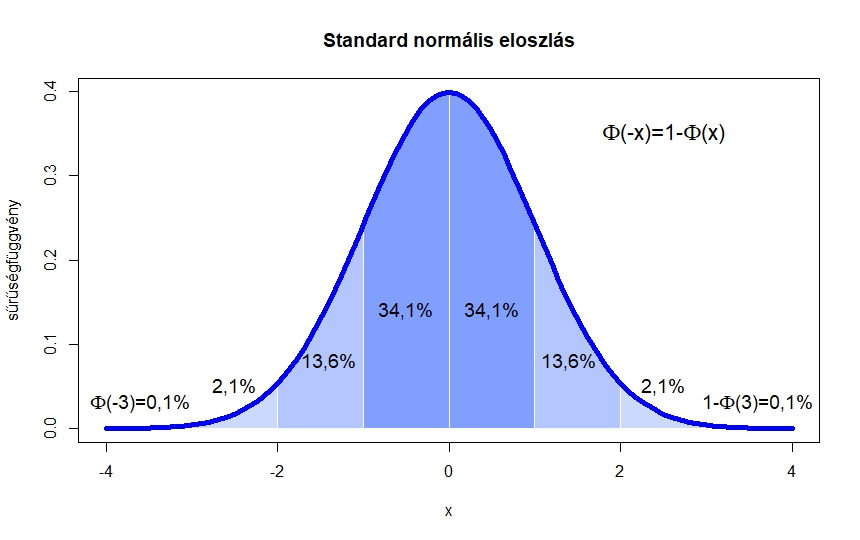
2. ábra. Az ![]() függvény és az alatta lévő területek
függvény és az alatta lévő területek
A fenti számolás általánosításával oda jutunk, hogy megfelelő feltételeket teljesítő ![]() számsorozatokra:
számsorozatokra:
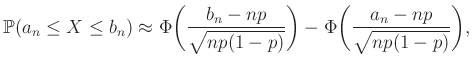 |
(5) |
hiszen a különbség nem más, mint a két érték közötti integrál. A példában pedig (az octave-ban ![]() a normcdf(x) paranccsal kapható meg):
a normcdf(x) paranccsal kapható meg):
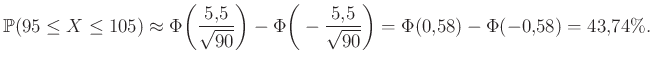
A (3) egyenlettel összehasonlítva látható, hogy továbbra is jó közelítést kaptunk.
4. Kapcsolat a centrális határeloszlás-tétellel és a normális eloszlással
Ezt a közelítő számolást precízzé téve juthatnánk el a de Moivre–Laplace-tétel globális alakjához (vagy annak általánosabb formájához, a centrális határeloszlás-tételhez [2], [3], [4], [8], [9]), és ebből a „megfelelő feltételek” is kiderülnek. A tételből ugyanis az következik, hogy rögzített ![]() valós számok és rögzített
valós számok és rögzített ![]() esetén, ha
esetén, ha ![]() binomiális eloszlású
binomiális eloszlású ![]() renddel és
renddel és ![]() paraméterrel, akkor
paraméterrel, akkor
Ha tehát rögzített ![]() és
és ![]() mellett
mellett
akkor a fenti közelítésben ![]() határértéket véve pontos egyenlőséget kapunk. Ebből az is látható, hogy ezzel a módszerrel a várható értéktől való
határértéket véve pontos egyenlőséget kapunk. Ebből az is látható, hogy ezzel a módszerrel a várható értéktől való ![]() nagyságrendű eltérések valószínűségét tudjuk jól meghatározni (ami éppen a binomiális eloszlás szórásának a nagyságrendje). A centrális határeloszlás-tétel abban általánosabb, hogy nem csak a binomiális eloszlásról, hanem tetszőleges független azonos eloszlású, véges szórású valószínűségi változók összegéről szól, és arról látja be, hogy a várható értéktől való
nagyságrendű eltérések valószínűségét tudjuk jól meghatározni (ami éppen a binomiális eloszlás szórásának a nagyságrendje). A centrális határeloszlás-tétel abban általánosabb, hogy nem csak a binomiális eloszlásról, hanem tetszőleges független azonos eloszlású, véges szórású valószínűségi változók összegéről szól, és arról látja be, hogy a várható értéktől való ![]() nagyságrendű eltérések limesze a fentihez hasonlóan a standard normális eloszlásfüggvénnyel írhatók le.
nagyságrendű eltérések limesze a fentihez hasonlóan a standard normális eloszlásfüggvénnyel írhatók le.
A közelítés hibája is felülről korlátozható, erre többféle lehetőség is van. Ennek egy egyszerű, bár nem a legjobb becslést adó alakja, ami a centrális határeloszlás egy még erősebb változatából, a Berry–Esséen-tételből [4] kapható, azt mondja, hogy a fenti közelítésénél (csak az egyik tagot tekintve) legfeljebb ![]() hibát követünk el. Ebből az mindenképpen fontos, hogy ha
hibát követünk el. Ebből az mindenképpen fontos, hogy ha ![]() közel van nullához, azaz
közel van nullához, azaz ![]() vagy
vagy ![]() túl kicsi az
túl kicsi az ![]() -hez képest, akkor a közelítés elromolhat. Ezért ennek a módszernek az alkalmazásánál például azt a feltételt szokták előírni, hogy
-hez képest, akkor a közelítés elromolhat. Ezért ennek a módszernek az alkalmazásánál például azt a feltételt szokták előírni, hogy ![]() teljesüljön [9]. Mivel
teljesüljön [9]. Mivel ![]() várható értéke
várható értéke ![]() , ez nem jelent sokkal többet, mint hogy legyen akkora az
, ez nem jelent sokkal többet, mint hogy legyen akkora az ![]() , hogy legalább
, hogy legalább ![]() védett embert találjunk.
védett embert találjunk.
Végül röviden arról, hogy mi is a standard normális eloszlás, aminek eloszlásfüggvénye ![]() . Ez egy olyan valószínűségi változó, amire az igaz tetszőleges
. Ez egy olyan valószínűségi változó, amire az igaz tetszőleges ![]() esetén, hogy
esetén, hogy ![]() valószínűséggel esik az
valószínűséggel esik az ![]() és
és ![]() számok közé, és ilyen módon
számok közé, és ilyen módon ![]() valószínűséggel lesz kisebb
valószínűséggel lesz kisebb ![]() -nél. Ahhoz, hogy egy ilyen
-nél. Ahhoz, hogy egy ilyen ![]() valószínűségi változót kapjunk, nem kell mást tenni, mint a 2. ábrán látható görbe alatti,
valószínűségi változót kapjunk, nem kell mást tenni, mint a 2. ábrán látható görbe alatti, ![]() nagyságú területről kiválasztani egy pontot „egyenletesen”, véletlenszerűen, majd
nagyságú területről kiválasztani egy pontot „egyenletesen”, véletlenszerűen, majd ![]() -nek ennek a pontnak a vízszintes tengelyre eső koordinátáját választani. A centrális határeloszlás-tétel pedig úgy is fogalmazható, hogy az
-nek ennek a pontnak a vízszintes tengelyre eső koordinátáját választani. A centrális határeloszlás-tétel pedig úgy is fogalmazható, hogy az ![]() valószínűségi változó „hasonlóan viselkedik” a standard normális eloszláshoz.
valószínűségi változó „hasonlóan viselkedik” a standard normális eloszláshoz.
5. A szükséges tesztek száma
Az előzőek alapján már közelítő választ tudunk adni az alábbi kérdésre.
Kérdés. Tegyük fel, hogy ![]() embert megvizsgálva mindenki egymástól függetlenül
embert megvizsgálva mindenki egymástól függetlenül ![]() valószínűséggel védett. Mekkorára válasszuk
valószínűséggel védett. Mekkorára válasszuk ![]() -t, hogy annak valószínűsége, hogy az elvégzett tesztek eredménye alapján adott becslésünknek és
-t, hogy annak valószínűsége, hogy az elvégzett tesztek eredménye alapján adott becslésünknek és ![]() -nek a különbsége legfeljebb
-nek a különbsége legfeljebb ![]() , legalább
, legalább ![]() legyen?
legyen?
Legyen továbbra is ![]() az, hogy az
az, hogy az ![]() elvégzett teszt közül hány mutat ki védettséget. A becslésünk továbbra is az
elvégzett teszt közül hány mutat ki védettséget. A becslésünk továbbra is az ![]() relatív gyakoriság lesz. A kérdés feltételét a következőképpen fogalmazhatjuk meg, az (1) egyenletből kiindulva:
relatív gyakoriság lesz. A kérdés feltételét a következőképpen fogalmazhatjuk meg, az (1) egyenletből kiindulva:
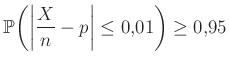 minden
minden A feltétel kicsit más, mint az előző részben, ott ugyanis a relatív hibát adtuk meg (![]() -nek hányadrésze lehet az eltérés), most viszont az abszolút hibát (legfeljebb milyen messze lehet a becslés
-nek hányadrésze lehet az eltérés), most viszont az abszolút hibát (legfeljebb milyen messze lehet a becslés ![]() -től). A relatív hiba esetére később még visszatérünk, ahogy érintőlegesen arra az esetre is, ha esetleg
-től). A relatív hiba esetére később még visszatérünk, ahogy érintőlegesen arra az esetre is, ha esetleg ![]() -ről van valamilyen előzetes információnk. A kérdés egyelőre abból indul ki, hogy olyan módszert keresünk, ami az ismeretlen
-ről van valamilyen előzetes információnk. A kérdés egyelőre abból indul ki, hogy olyan módszert keresünk, ami az ismeretlen ![]() valószínűség minden értékére jó, holott természetesen nem biztos, hogy ugyanaz a módszer lenne egyformán hatékony egy ezrelékes vagy tízszázalékos védettségi arány esetén.
valószínűség minden értékére jó, holott természetesen nem biztos, hogy ugyanaz a módszer lenne egyformán hatékony egy ezrelékes vagy tízszázalékos védettségi arány esetén.
A fenti valószínűséget alakítsuk át a korábban látott (5) közelítésnek megfelelően (az ![]() -re vonatkozó „megfelelő feltételeket” egyelőre figyelmen kívül hagyva):
-re vonatkozó „megfelelő feltételeket” egyelőre figyelmen kívül hagyva):
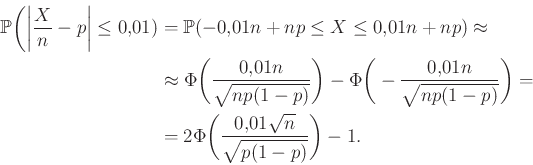 |
(6) |
Az utolsó lépés abból adódik, hogy a 2. ábrán látható haranggörbe 0-ra való szimmetriája miatt a ![]() -től balra lévő terület, vagyis
-től balra lévő terület, vagyis ![]() ugyanaz, mint a
ugyanaz, mint a ![]() -től jobbra lévő, mivel viszont a teljes görbe alatti terület
-től jobbra lévő, mivel viszont a teljes görbe alatti terület ![]() , ez utóbbi nem más, mint
, ez utóbbi nem más, mint ![]() .
.
Tehát azt szeretnénk elérni, hogy minden ![]() -re
-re
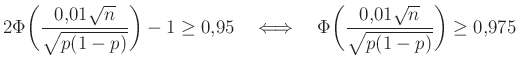 |
(7) |
teljesüljön. Vagyis a törtnek olyan értéket kell felvennie, amire igaz, hogy a 2. ábrán a tőle balra eső terület legalább ![]() . Az ábrán azt látjuk, hogy a
. Az ábrán azt látjuk, hogy a ![]() -től balra eső terület éppen 1 – 0,022 = 0,978. Vagyis a
-től balra eső terület éppen 1 – 0,022 = 0,978. Vagyis a ![]() -nél nagyobb számok biztosan jók, az ennél sokkal kisebbek nem. A pontos határ, amit az octave-ban a norminv(0.975) paranccsal számíthatunk ki (az átrendezés pedig azért érvényes, mert
-nél nagyobb számok biztosan jók, az ennél sokkal kisebbek nem. A pontos határ, amit az octave-ban a norminv(0.975) paranccsal számíthatunk ki (az átrendezés pedig azért érvényes, mert ![]() monoton növő függvény):
monoton növő függvény):
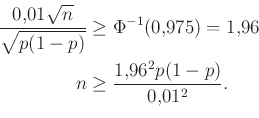 |
(8) |
Tehát, ha ez a feltétel teljesül, és a közelítések során nem vétettünk túl nagy hibát, akkor ez megadja, hogy legalább hány teszt elvégzésre van szükség. Azonban ![]() -t, ami a védettek valódi aránya, nem ismerjük, pont ezt szeretnénk megbecsülni, így a feltételnek minden
-t, ami a védettek valódi aránya, nem ismerjük, pont ezt szeretnénk megbecsülni, így a feltételnek minden ![]() -re teljesülnie kell. Szerencsére
-re teljesülnie kell. Szerencsére ![]() nem lehet bármilyen nagy (ez
nem lehet bármilyen nagy (ez ![]() függvényeként egy parabola, aminek van maximuma), például a számtani-mértani közepek közti egyenlőtlenség alapján
függvényeként egy parabola, aminek van maximuma), például a számtani-mértani közepek közti egyenlőtlenség alapján ![]() , és pontos egyenlőség is van,
, és pontos egyenlőség is van, ![]() esetén. Vagyis a szükséges mintaelemszám, amivel a feltételünk már minden
esetén. Vagyis a szükséges mintaelemszám, amivel a feltételünk már minden ![]() -re teljesül:
-re teljesül:
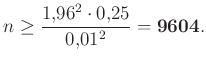
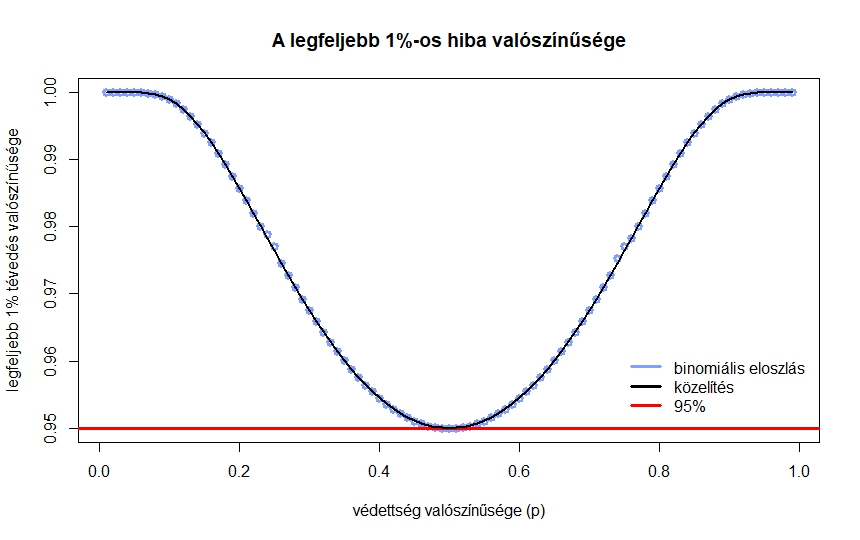
3. ábra. Annak valószínűsége, hogy legfeljebb ![]() -ot téved a becslés, a valós
-ot téved a becslés, a valós ![]() védettségi arány függvényében,
védettségi arány függvényében, ![]() teszt esetén
teszt esetén
Ezt adja tehát a módszerünk a fent megfogalmazott kérdésre. A közelítés után már csak ekvivalens átalakításokat végeztünk, ezért ha a kiindulás helyes volt, akkor ennél kisebb ![]() nem is lehet jó. Azt is láthatjuk, hogy ha
nem is lehet jó. Azt is láthatjuk, hogy ha ![]() -ről valamilyen előzetes információnk van, például biztosan tudjuk, hogy legfeljebb
-ről valamilyen előzetes információnk van, például biztosan tudjuk, hogy legfeljebb ![]() , akkor kisebb minta is elég, hiszen ekkor
, akkor kisebb minta is elég, hiszen ekkor ![]() -re az
-re az ![]() helyett jobb felső becslést írhatunk a (8) egyenlőtlenségben.
helyett jobb felső becslést írhatunk a (8) egyenlőtlenségben.
Viszont a közelítés miatt mindenképpen szükséges valamiféle ellenőrzés. A 3. ábrán az látható, hogy ha a tesztek száma ![]() , akkor a különböző
, akkor a különböző ![]() értékekre mennyi
értékekre mennyi ![]() — vagyis mennyi annak valószínűsége, hogy legfeljebb
— vagyis mennyi annak valószínűsége, hogy legfeljebb ![]() -ot tévedünk. A binomiális eloszlásból számolt értékek mellett a normális eloszlásből a (7) közelítő képlet eredményét is ábrázoltuk, jól látható, hogy a két görbe egymásra illeszkedik (a binomiális eloszlásnál nem a korábban látott közvetlen számolást, hanem a szoftverek beépített függvényeit alkalmaztuk, ezek a kerekítésekből adódó hibákat a lehető legjobban elkerülik). Az ábra alapján megállapíthatjuk, hogy
-ot tévedünk. A binomiális eloszlásból számolt értékek mellett a normális eloszlásből a (7) közelítő képlet eredményét is ábrázoltuk, jól látható, hogy a két görbe egymásra illeszkedik (a binomiális eloszlásnál nem a korábban látott közvetlen számolást, hanem a szoftverek beépített függvényeit alkalmaztuk, ezek a kerekítésekből adódó hibákat a lehető legjobban elkerülik). Az ábra alapján megállapíthatjuk, hogy ![]() esetén valóban tetszőleges
esetén valóban tetszőleges ![]() -re legalább
-re legalább ![]() valószínűséggel az előírt hibahatáron belüli a becslésünk, viszont ebben az esetben
valószínűséggel az előírt hibahatáron belüli a becslésünk, viszont ebben az esetben ![]() esetén egyenlőség lenne, ami azt jelenti, hogy kisebb mintaelemszám már nem elegendő (
esetén egyenlőség lenne, ami azt jelenti, hogy kisebb mintaelemszám már nem elegendő (![]() teszt és
teszt és ![]() esetén annak valószínűsége, hogy legfeljebb
esetén annak valószínűsége, hogy legfeljebb ![]() -ot tévedünk, „csak”
-ot tévedünk, „csak” ![]() ).
).
6. A relatív hiba, kis p esete és a pontosságtól való függés
Az ábrán azt is érdemes megfigyelni, hogy kicsi vagy egyhez közeli ![]() esetén (ahol pedig egyébként a (4) egyenlet közelítése elromlik), jobbnak tűnik a helyzet, mint amikor
esetén (ahol pedig egyébként a (4) egyenlet közelítése elromlik), jobbnak tűnik a helyzet, mint amikor ![]() közel van
közel van ![]() -hez (a szimmetria természetes, hiszen mindegy, hogy a védettek vagy a nem védettek arányára vagyunk kíváncsiak). Azonban vegyük észre, hogy az abszolút eltérésre fogalmaztuk meg a feltételt. Vagyis ebbe az is belefér, hogy
-hez (a szimmetria természetes, hiszen mindegy, hogy a védettek vagy a nem védettek arányára vagyunk kíváncsiak). Azonban vegyük észre, hogy az abszolút eltérésre fogalmaztuk meg a feltételt. Vagyis ebbe az is belefér, hogy ![]() helyett a becslésünk
helyett a becslésünk ![]() legyen – ez legfeljebb
legyen – ez legfeljebb ![]() -nyi különbség, mégis tízszeres relatív hiba az igazi
-nyi különbség, mégis tízszeres relatív hiba az igazi ![]() -hez képest. Vagyis arra is következtethetünk, hogy kisebb (vagy éppen egyhez közelebbi)
-hez képest. Vagyis arra is következtethetünk, hogy kisebb (vagy éppen egyhez közelebbi) ![]() értékeket csak nagyobb mintaelemszámmal tudunk megbecsülni. Ha a
értékeket csak nagyobb mintaelemszámmal tudunk megbecsülni. Ha a ![]() -hez számított relatív hibát adjuk meg, akkor
-hez számított relatív hibát adjuk meg, akkor ![]() helyére
helyére ![]() kerül, és ha visszatérünk a (8) egyenlethez, akkor
kerül, és ha visszatérünk a (8) egyenlethez, akkor ![]() lesz az alsó becslés
lesz az alsó becslés ![]() -re. Vagyis a szükséges mintaelemszám a
-re. Vagyis a szükséges mintaelemszám a ![]() -vel nagyjából fordítottan arányosan tart végtelenhez. Ezt az alábbi táblázat mutatja néhány konkrét érték esetén (itt tehát mindig csak az látszik, hogy ha az adott
-vel nagyjából fordítottan arányosan tart végtelenhez. Ezt az alábbi táblázat mutatja néhány konkrét érték esetén (itt tehát mindig csak az látszik, hogy ha az adott ![]() -re teljesíteni akarjuk a feltételt, akkor mekkora
-re teljesíteni akarjuk a feltételt, akkor mekkora ![]() -re van szükség):
-re van szükség):
| relatív hiba ( |
|||
| |
|||
| |
|
|
|
| |
|
|
A táblázatból jól látszik, hogy a relatív hibát alacsonyan tartani kicsi vagy egyhez közeli ![]() esetén jóval nehezebb lehet, mint
esetén jóval nehezebb lehet, mint ![]() -hez közelebbi
-hez közelebbi ![]() esetén. A táblázat értékeit a fent bemutatott normális közelítéssel számoltuk, de feltüntettük zárójelben, hogy ez mennyivel tér el a valódi értéktől. Ezzel tehát a közelítésünk pontosságáról is képet kaphatunk. A táblázat és az előző képlet pedig együtt azt is sugallják, hogy ha előzetesen nem tudunk egy biztos alsó becslést
esetén. A táblázat értékeit a fent bemutatott normális közelítéssel számoltuk, de feltüntettük zárójelben, hogy ez mennyivel tér el a valódi értéktől. Ezzel tehát a közelítésünk pontosságáról is képet kaphatunk. A táblázat és az előző képlet pedig együtt azt is sugallják, hogy ha előzetesen nem tudunk egy biztos alsó becslést ![]() -re (például hogy
-re (például hogy ![]() ), akkor nem is tudunk megfelelő mintaelemszámot mondani a relatív hiba adott korlát alatt tartásához. Ez persze onnan is látható, hogy minél kisebb a
), akkor nem is tudunk megfelelő mintaelemszámot mondani a relatív hiba adott korlát alatt tartásához. Ez persze onnan is látható, hogy minél kisebb a ![]() , annál többet kell várnunk arra, hogy akár csak egyetlen védett embert is találjunk. Amíg pedig ilyen nincs, addig csak felső becslést tudunk adni a védettség valószínűségére, alsó becslésre és pontos értékre nem számíthatunk.
, annál többet kell várnunk arra, hogy akár csak egyetlen védett embert is találjunk. Amíg pedig ilyen nincs, addig csak felső becslést tudunk adni a védettség valószínűségére, alsó becslésre és pontos értékre nem számíthatunk.
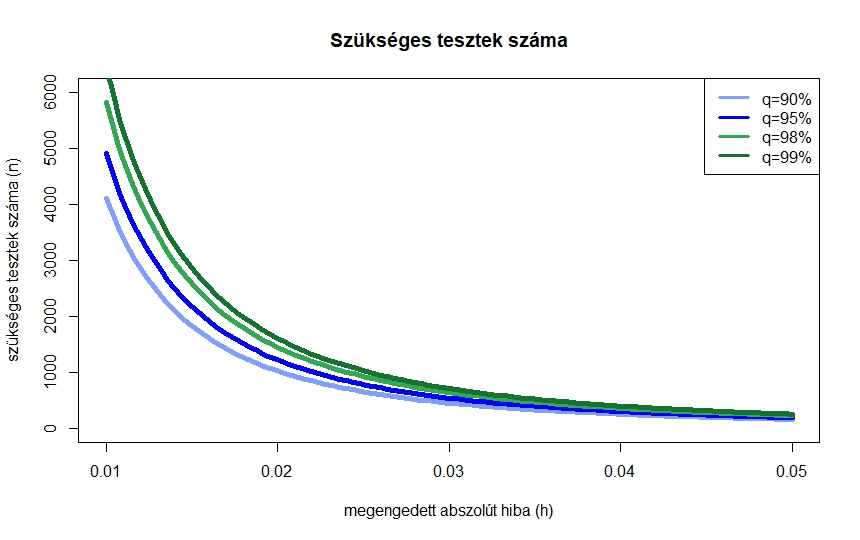
4. ábra. A szükséges tesztek száma normális közelítéssel néhány megbízhatósági szint mellett a megengedett abszolút hiba függvényében
A kapott összefüggést általánosan felírva megvizsgálhatjuk, hogy hogyan függ a szükséges mintaelemszám értéke az előírt feltételektől. Az előző számolással teljesen hasonló módon az adódik, hogy ha azt szeretnénk, legalább ![]() valószínűséggel legfeljebb
valószínűséggel legfeljebb ![]() -t tévedjünk, akkor a fenti (6) közelítéssel a szükséges tesztek száma (visszatérve a
-t tévedjünk, akkor a fenti (6) közelítéssel a szükséges tesztek száma (visszatérve a ![]() abszolút hibára):
abszolút hibára):
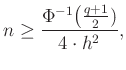
ahol tehát ![]() , és ennek az inverzére van szükség (az octave-ban norminv). Az ebből könnyen látszik, hogy mivel az előírt
, és ennek az inverzére van szükség (az octave-ban norminv). Az ebből könnyen látszik, hogy mivel az előírt ![]() hibahatárnak a négyzete szerepel a nevezőben, kétszer akkora pontossághoz négyszer annyi mérés kell. A 4. ábra ezt az összefüggést mutatja néhány különböző
hibahatárnak a négyzete szerepel a nevezőben, kétszer akkora pontossághoz négyszer annyi mérés kell. A 4. ábra ezt az összefüggést mutatja néhány különböző ![]() érték esetén. Az ábrán az is látszik, hogy a megbízhatósági szinttől,
érték esetén. Az ábrán az is látszik, hogy a megbízhatósági szinttől, ![]() -tól való függés kevésbé erős,
-tól való függés kevésbé erős, ![]() -os megbízhatósághoz nem lesz szükség nagyságrendekkel több tesztre, mint
-os megbízhatósághoz nem lesz szükség nagyságrendekkel több tesztre, mint ![]() -oshoz. Persze, ahogy az ábra alapján is sejthető és a képletből következik, az igaz, hogy ha
-oshoz. Persze, ahogy az ábra alapján is sejthető és a képletből következik, az igaz, hogy ha ![]() , akkor a szükséges tesztek száma végtelenhez tart:
, akkor a szükséges tesztek száma végtelenhez tart: ![]() az a szám, amitől balra a 2. ábrán
az a szám, amitől balra a 2. ábrán ![]() terület van. De mivel a teljes görbe alatti terület
terület van. De mivel a teljes görbe alatti terület ![]() , ez az érték végtelenhez tart, ahogy
, ez az érték végtelenhez tart, ahogy ![]() . Ezek a jelenségek a cikkünk második részében is előjönnek majd, amikor konfidenciaintervallumot adunk meg, vagyis egy olyan intervallumot, ami nagy valószínűséggel tartalmazza a valódi
. Ezek a jelenségek a cikkünk második részében is előjönnek majd, amikor konfidenciaintervallumot adunk meg, vagyis egy olyan intervallumot, ami nagy valószínűséggel tartalmazza a valódi ![]() -t.
-t.
7. Elmélet és gyakorlat
A fentiekben tehát a binomiális eloszlás normális közelítésének segítségével meghatároztuk, hogy ahhoz, hogy adott valószínűséggel adott hibahatáron belül legyen a becslésünk, hány teszt szükséges. Végül azt vizsgáljuk meg, hogy a feltevéseink közül mi az, ami a valóságban is könnyen teljesíthető, és mi az, ami további vizsgálatot igényelne.
![]() Függetlenség. Az egyik feltételezésünk az volt, hogy a tesztek eredménye egymástól független. A vizsgálatba bevont személyek kiválasztásánál ezt könnyű majdnem tökéletesen teljesíteni: ha sorban haladva mindig elfelejtenénk az eddig kiválasztottakat, és úgy választanánk a következő embert, akkor ez teljesülne, ha pedig figyelünk arra, hogy senkit ne válasszunk kétszer, akkor is ez a legtöbb esetben közelítőleg teljesül. Ugyanis mondjuk 2000000 ember közül 10000-t az még könnyen előfordulhat, hogy néhányan többször is szerepelnek, de arra már kevés az esély, hogy valakit olyan sokszor választunk, hogy ettől a mintavételezés eredménye is lényegesen megváltozik a csupa különböző ember esetéhez képest (ez a binomiális eloszlás hipergeometrikus eloszlással való közelítése, [9]). A mérések során ez a feltétel azt jelenti, hogy az egymás után, esetleg párhuzamosan, csoportosítva végzett eljárások eredménye között se legyen összefüggés.
Függetlenség. Az egyik feltételezésünk az volt, hogy a tesztek eredménye egymástól független. A vizsgálatba bevont személyek kiválasztásánál ezt könnyű majdnem tökéletesen teljesíteni: ha sorban haladva mindig elfelejtenénk az eddig kiválasztottakat, és úgy választanánk a következő embert, akkor ez teljesülne, ha pedig figyelünk arra, hogy senkit ne válasszunk kétszer, akkor is ez a legtöbb esetben közelítőleg teljesül. Ugyanis mondjuk 2000000 ember közül 10000-t az még könnyen előfordulhat, hogy néhányan többször is szerepelnek, de arra már kevés az esély, hogy valakit olyan sokszor választunk, hogy ettől a mintavételezés eredménye is lényegesen megváltozik a csupa különböző ember esetéhez képest (ez a binomiális eloszlás hipergeometrikus eloszlással való közelítése, [9]). A mérések során ez a feltétel azt jelenti, hogy az egymás után, esetleg párhuzamosan, csoportosítva végzett eljárások eredménye között se legyen összefüggés.
![]() Azonos védettségi valószínűség. Feltételeztük, hogy minden ember azonos
Azonos védettségi valószínűség. Feltételeztük, hogy minden ember azonos ![]() valószínűséggel védett. Ez egyrészt azt jelenti, hogy a védettek aránya a lakosságban ne változzon jelentősen a tesztek elvégzésének időszaka alatt, ami akár egy-két hét is lehet. Másrészt, ha további tulajdonságokat is figyelembe veszünk (például a lakóhelyet, vagy hogy volt-e az illető mostanában beteg), akkor ez természetesen nem teljesül, de ez nem baj, amíg megelégszünk azzal, hogy az átlagos védettségi valószínűséget vizsgáljuk, és nem az egyes csoportokét külön-külön. Annak valószínűsége ugyanis, hogy egy véletlenszerűen választott ember védett, éppen az átlagos védettségi valószínűség.
valószínűséggel védett. Ez egyrészt azt jelenti, hogy a védettek aránya a lakosságban ne változzon jelentősen a tesztek elvégzésének időszaka alatt, ami akár egy-két hét is lehet. Másrészt, ha további tulajdonságokat is figyelembe veszünk (például a lakóhelyet, vagy hogy volt-e az illető mostanában beteg), akkor ez természetesen nem teljesül, de ez nem baj, amíg megelégszünk azzal, hogy az átlagos védettségi valószínűséget vizsgáljuk, és nem az egyes csoportokét külön-külön. Annak valószínűsége ugyanis, hogy egy véletlenszerűen választott ember védett, éppen az átlagos védettségi valószínűség.
![]() Egyenletes választás. Itt azonban nagyon nem mindegy, hogy a „véletlenszerűen” és az „átlagos” mire vonatkozik. Ideális esetben az átlagban mondjuk egy ország minden lakosa azonos súllyal szerepel. Azt azonban, hogy úgy végezzük a vizsgálatot, hogy mindenkit azonos valószínűséggel válasszunk, legalább annyira nehéz megvalósítani, mint amilyen könnyű leírni. Ha az, hogy valaki védett-e, nem függne attól, hogy milyen könnyű őt egy ilyen vizsálatba bevonni, ez sem jelentene problémát – de leggyakrabban ezt nem tételezhetjük fel. Ennek az úgynevezett mintavételi torzításnak a kiküszöbölésére egy szokásos eljárás az, hogy ha mondjuk a mintában több budapesti ember szerepel, mint amennyi a budapestiek valós aránya, akkor a budapestiek és a vidékiek esetében is külön kiszámítják az átlagot, majd pontosabb (például népszámlálási) adatok alapján ezeket olyan súlyokkal veszik figyelembe, ami ezeknek a csoportoknak a valódi aránya lenne (bővebben például: [5]).
Egyenletes választás. Itt azonban nagyon nem mindegy, hogy a „véletlenszerűen” és az „átlagos” mire vonatkozik. Ideális esetben az átlagban mondjuk egy ország minden lakosa azonos súllyal szerepel. Azt azonban, hogy úgy végezzük a vizsgálatot, hogy mindenkit azonos valószínűséggel válasszunk, legalább annyira nehéz megvalósítani, mint amilyen könnyű leírni. Ha az, hogy valaki védett-e, nem függne attól, hogy milyen könnyű őt egy ilyen vizsálatba bevonni, ez sem jelentene problémát – de leggyakrabban ezt nem tételezhetjük fel. Ennek az úgynevezett mintavételi torzításnak a kiküszöbölésére egy szokásos eljárás az, hogy ha mondjuk a mintában több budapesti ember szerepel, mint amennyi a budapestiek valós aránya, akkor a budapestiek és a vidékiek esetében is külön kiszámítják az átlagot, majd pontosabb (például népszámlálási) adatok alapján ezeket olyan súlyokkal veszik figyelembe, ami ezeknek a csoportoknak a valódi aránya lenne (bővebben például: [5]).
![]() A tesztek megbízhatósága. Végig úgy számoltunk, hogy a tesztek sosem hibáznak. Ez természetesen a valóságban nincs így, és, főleg kis védettségi valószínűség esetén, még az is nagyon könnyen előfordulhat, hogy a hamis pozitív tesztek száma több, mint valódi pozitívaké. Hiszen ha mondjuk
A tesztek megbízhatósága. Végig úgy számoltunk, hogy a tesztek sosem hibáznak. Ez természetesen a valóságban nincs így, és, főleg kis védettségi valószínűség esetén, még az is nagyon könnyen előfordulhat, hogy a hamis pozitív tesztek száma több, mint valódi pozitívaké. Hiszen ha mondjuk ![]() ember közül csak
ember közül csak ![]() védett valójában, akkor a tesztnek körülbelül
védett valójában, akkor a tesztnek körülbelül ![]() -os valószínűségű tévedése is elég ahhoz, hogy legyen majdnem
-os valószínűségű tévedése is elég ahhoz, hogy legyen majdnem ![]() ember, akit hamisan védettnek gondolunk, és hogy a védettség valószínűségét háromszorosan túlbecsüljük. Ez a bizonytalanság, amit információs vagy mérési torzításnak neveznek, mint minden információhiány, azonban feltehetően csak növelné a szükséges tesztek számát, így ebből a szempontból a fenti értékeket alsó becslésnek tekinthetjük. Ennek a hibának a kiküszöbölése az epidemiológiának fontos témaköre, további hibalehetőségek figyelembevételével együtt [10].
ember, akit hamisan védettnek gondolunk, és hogy a védettség valószínűségét háromszorosan túlbecsüljük. Ez a bizonytalanság, amit információs vagy mérési torzításnak neveznek, mint minden információhiány, azonban feltehetően csak növelné a szükséges tesztek számát, így ebből a szempontból a fenti értékeket alsó becslésnek tekinthetjük. Ennek a hibának a kiküszöbölése az epidemiológiának fontos témaköre, további hibalehetőségek figyelembevételével együtt [10].
![]() A közelítésből adódó hiba. A fenti levezetésben egy közelítést alkalmaztunk, és nem bizonyítottuk, csak számítógéppel ellenőriztük, hogy a megadott szám valóban elég sok tesztet jelent. Ezen például a már említett Berry–Esséen-tétel vagy ennél is pontosabb becslések alapján lehetne javítani. Ugyanakkor ezekből állításokból is látszik, hogy a normális eloszlással való közelítés elromlik, ha
A közelítésből adódó hiba. A fenti levezetésben egy közelítést alkalmaztunk, és nem bizonyítottuk, csak számítógéppel ellenőriztük, hogy a megadott szám valóban elég sok tesztet jelent. Ezen például a már említett Berry–Esséen-tétel vagy ennél is pontosabb becslések alapján lehetne javítani. Ugyanakkor ezekből állításokból is látszik, hogy a normális eloszlással való közelítés elromlik, ha ![]() közel van nullához vagy egyhez. Ilyenkor egy másik lehetőség a Poisson-eloszlással való közelítés lenne [3], [9], de az érvényes marad, hogy ha a relatív hibát is alacsonyan akarjuk tartani, akkor jóval több tesztre lehet szükség. Arra bizonyítást adni, hogy egy adott számú minta már elég a megadott pontossághoz, egyszerűbb módszerekkel, például a Csebisev-egyenlőtlenséggel [2], [3], [9] is lehetséges. Ez azt állítja, hogy annak valószínűsége, hogy egy valószínűségi változó legalább
közel van nullához vagy egyhez. Ilyenkor egy másik lehetőség a Poisson-eloszlással való közelítés lenne [3], [9], de az érvényes marad, hogy ha a relatív hibát is alacsonyan akarjuk tartani, akkor jóval több tesztre lehet szükség. Arra bizonyítást adni, hogy egy adott számú minta már elég a megadott pontossághoz, egyszerűbb módszerekkel, például a Csebisev-egyenlőtlenséggel [2], [3], [9] is lehetséges. Ez azt állítja, hogy annak valószínűsége, hogy egy valószínűségi változó legalább ![]() -vel tér el a saját várható értékétől, legfeljebb a szórásnégyzetének és
-vel tér el a saját várható értékétől, legfeljebb a szórásnégyzetének és ![]() -nek a hányadosa. Ez a megközelítés azonban olyan egyenlőtlenséget használ, ami minden eloszlásra egyaránt érvényes, és ha speciálisan a binomiális eloszlásra alkalmazzuk, akkor nem túl erős. Konkrétan a
-nek a hányadosa. Ez a megközelítés azonban olyan egyenlőtlenséget használ, ami minden eloszlásra egyaránt érvényes, és ha speciálisan a binomiális eloszlásra alkalmazzuk, akkor nem túl erős. Konkrétan a ![]() hiba és
hiba és ![]() megbízhatóság mellett ebből az jönne ki, hogy
megbízhatóság mellett ebből az jönne ki, hogy ![]() elég, ami igaz, de azt láttuk, hogy valójában az ötödénél is kevesebb,
elég, ami igaz, de azt láttuk, hogy valójában az ötödénél is kevesebb, ![]() teszt már elég ugyanehhez.
teszt már elég ugyanehhez.
8. Következik: konfidenciaintervallum és maximumlikelihood-becslés
Összességében tehát a fenti matematikai módszerek alkalmazása során egy jól megbízható teszt és a vizsgálatba bevont személyek megfelelően elvégzett kiválasztása mellett számoltunk, közelítő módszerekkel, ahol azonban a közelítés jól működik, amíg a védettek valódi aránya sem nem túl kicsi, sem nem túl nagy a mintaelemszámhoz képest. Ez tehát arra mindenképpen hasznos, hogy lássuk, hogy mi az a szám, aminél semmiképpen nem mehetünk lejjebb az elvégzett tesztek számával adott pontosság mellett. Továbbá azt is megállapíthattuk, hogy a pontosság növelése milyen ütemben növeli a szükséges tesztek számát, és arra is több szempontot láttunk, hogy miért van szükség több tesztre, ha a védettek valódi aránya kicsi, és a relatív hibát akarjuk alacsonyan tartani.
Cikkünk második részében egyrészt arra térünk majd ki, hogy a fenti módszer arra is használható, hogy adott mintaelemszám esetén megfogalmazzuk, hogy mennyire vagyunk biztosak a ![]() -re vonatkozó becslésünkben, amire egy szokásos módszer a konfidenciaintervallum megadása. Ez egy olyan intervallum, ami az ismeretlen
-re vonatkozó becslésünkben, amire egy szokásos módszer a konfidenciaintervallum megadása. Ez egy olyan intervallum, ami az ismeretlen ![]() értéket nagy valószínűséggel tartalmazza (bár, mint látni fogjuk, ez nem pontosan azt jelenti, amit elsőre gondolnánk, ugyanis az eddig használt statisztikai felépítést követve
értéket nagy valószínűséggel tartalmazza (bár, mint látni fogjuk, ez nem pontosan azt jelenti, amit elsőre gondolnánk, ugyanis az eddig használt statisztikai felépítést követve ![]() -t továbbra sem tekintjük véletlennek). A fenti módszeren alapuló számításokkal hasonló jelenségeket figyelhetünk majd meg, például hogy megfelelő feltételek mellett fele olyan hosszú konfidenciaintervallumhoz négyszer akkora minta szükséges, vagy hogy kis
-t továbbra sem tekintjük véletlennek). A fenti módszeren alapuló számításokkal hasonló jelenségeket figyelhetünk majd meg, például hogy megfelelő feltételek mellett fele olyan hosszú konfidenciaintervallumhoz négyszer akkora minta szükséges, vagy hogy kis ![]() esetén a konfidenciaintervallum végpontjainak aránya nagy lehet.
esetén a konfidenciaintervallum végpontjainak aránya nagy lehet.
Másrészt egy olyan statisztikai módszert is bemutatunk, amely amellett érvel, hogy minden vizsgált személyhez ugyanazt a ![]() védettségi valószínűséget feltételezve miért az
védettségi valószínűséget feltételezve miért az ![]() relatív gyakoriság a legjobb becslés, miért nem például
relatív gyakoriság a legjobb becslés, miért nem például ![]() (amit egy másik módszerrel, a Bayes-becsléssel kaphatnánk, megfelelő előzetes feltételezések mellett). Ezt maximumlikelihood-becslésnek hívják, és a tesztek nyelvén megfogalmazva az alábbi elvből indul ki. Tegyük fel, hogy a laboratóriumban két dobozban vannak tesztek, és arra is emlékszünk, hogy az egyik dobozban a jó tesztek voltak, amik a védettséget
(amit egy másik módszerrel, a Bayes-becsléssel kaphatnánk, megfelelő előzetes feltételezések mellett). Ezt maximumlikelihood-becslésnek hívják, és a tesztek nyelvén megfogalmazva az alábbi elvből indul ki. Tegyük fel, hogy a laboratóriumban két dobozban vannak tesztek, és arra is emlékszünk, hogy az egyik dobozban a jó tesztek voltak, amik a védettséget ![]() valószínűséggel kimutatják, a másikban a rosszak, amik csak
valószínűséggel kimutatják, a másikban a rosszak, amik csak ![]() valószínűséggel jelzik a védettséget. Csak éppen azt felejtettük el, hogy melyik doboz melyik. Ezért szerzünk néhány biztosan pozitív (védett embertől származó) mintát, és az egyik doboz tíz tesztjével megvizsgáljuk. A tíz mérésből 8 pozitív lett. Biztosak nem lehetünk, de ebben az esetben könnyű megmondani, hogy mire gondolnánk inkább, melyik doboz volt az, amit kipróbáltunk. Ez a gondolat vezet el tehát egy jóval általánosabb statisztikai módszerhez, melyet a következő részben a tesztelés példáján keresztül mutatunk majd be.
valószínűséggel jelzik a védettséget. Csak éppen azt felejtettük el, hogy melyik doboz melyik. Ezért szerzünk néhány biztosan pozitív (védett embertől származó) mintát, és az egyik doboz tíz tesztjével megvizsgáljuk. A tíz mérésből 8 pozitív lett. Biztosak nem lehetünk, de ebben az esetben könnyű megmondani, hogy mire gondolnánk inkább, melyik doboz volt az, amit kipróbáltunk. Ez a gondolat vezet el tehát egy jóval általánosabb statisztikai módszerhez, melyet a következő részben a tesztelés példáján keresztül mutatunk majd be.
Irodalomjegyzék
- [1] Douglas Altman, David Machin, Trevor Bryant, Martin Gardner, Statistics with Confidence: Confidence Intervals and Statistical Guidelines. Second Edition, John Wiley & Sons, New York, 2000.
[2] Arató Miklós, Prokaj Vilmos, Zempléni András, Bevezetés a valószínűségszámításba és alkalmazásaiba: példákkal, szimulációkkal, 2013. https://ttk.elte.hu/dstore/document/901/zempleni.pdf
[3] Csiszár Villő, Valószínűségszámítás 1. http://csvillo.web.elte.hu/mtval/jegyzet.pdf
[4] William Feller, An introduction to probability theory and its applications. Vol. I. Third edition, John Wiley & Sons, Inc., New York, 1968.
[5] David Freedman, Robert Pisani, Roger Purves, Statistics. Fourth edition, W. W. Norton & Company, New York, 2007.
[6] Pierre-Simon de Laplace, Théorie analytiques de probabilités. 3ème éd., revue et augmentée par l'auteur, Courcier, Paris, 1820.
[7] Abraham de Moivre, Miscellanea analytica de seriebus et quadraturis. Lib. 5. J. Tonson & J. Watts, London, 1730.
[8] Rényi Alfréd, Valószínűségszámítás. Tankönyvkiadó, Budapest, 1954.
[9] Sheldon Ross, A first course in probability. Second edition, Macmillan Co., New York, 1984.
[10] Kenneth J. Rothman, Epidemiology: An introduction. Se Oxford University Press, New York, 2012.
–









