Mastermind, bástyák és ismerősök

A Héttusa 17., 18. és 20. feladata továbbgondolható, olyan, amit érdemes számítógép segítségével is megvizsgálni.

17. Marci bástyákat rak egy üres sakktáblára. Akkor helyezhet el egy bástyát egy üres mezőre, ha annak legalább két oldalszomszédja üres. Legfeljebb hány bástyát helyezhet a táblára Marci?

Megoldás. 56-ot például így; itt a számok azt jelzik, hogy az adott mezőbe hányadik lépésben rakunk le bástyát:

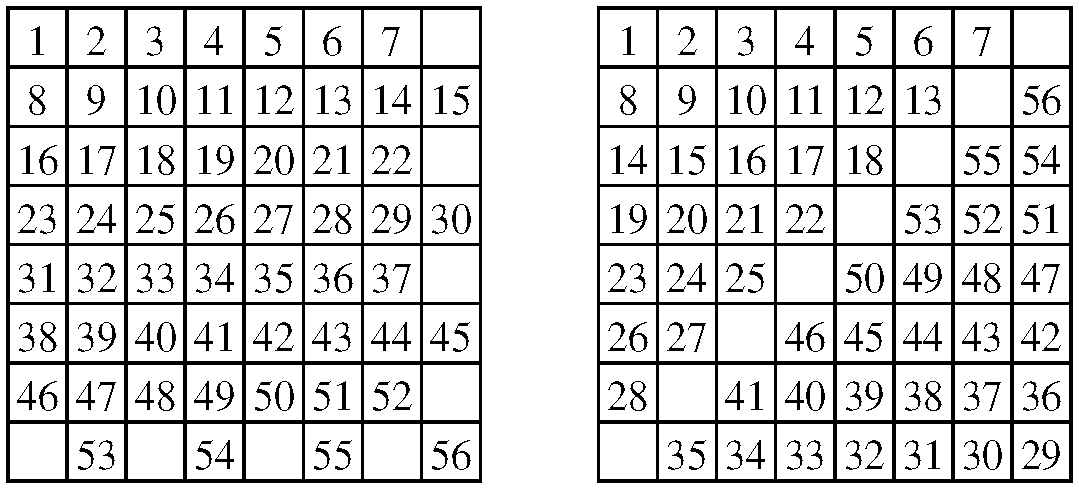
Hogy 56-nál több bástya nem helyezhető el, az belátható a mintamegoldás alapján is (lásd a Héttusa 3. fordulójának megoldásait). De a kitűző felhívta a szerző figyelmét egy ehhez kapcsolható feladatra:

Adott egy 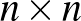$n\times n$ -es négyzetrács, amelynek minden négyzete vagy gyepes, vagy üres. Egy üres négyzet akkor válik gyepessé, ha legalább két szomszédja már gyepes. Egy gyepes négyzet mindig gyepes marad. Legalább hány négyzetnek kell gyepesnek lennie ahhoz, hogy a gyep átterjedjen az összes négyzetre?

Először is belátjuk, hogy a két probléma tényleg ekvivalens a következő értelemben: ha egy megfelelő bástyalerakásnál kimaradó mezőket tesszük gyepessé, akkor az át fog terjedni az összes négyzetre, illetve ha van egy megfelelő kiindulási gyepesítés, akkor a nem gyepes négyzetekre megfelelő sorrendben lehelyezhetőek a bástyák. Ehhez azt kell meggondolni, hogy egy új mező gyepesedése pontosan akkor történhet meg, ha a bástyalerakásos példánál annak a mezőnek két üres szomszédja van, és ezért oda lerakható a bástya. Másképpen fogalmazva (összevonva a két feladatot), a bástyákat csak „zöldmezős beruházás” keretei között lehet lerakni: eredetileg minden mező gyepes, és bástya akkor rakható le, ha legalább két szomszédja gyepes. De (mint minden emberi alkotás esetén) a természet igyekszik visszahódítani az elfoglalt területet: két gyepes szomszédból „a gyökerek feltörik a bástya alapját”, és abból a négyzetből ismét gyepes lesz. Vagyis a két probléma megoldása pontosan ugyanannak a folyamatnak az előre, illetve hátra történő végrehajtását jelenti. A fenti bástyaelhelyezések például a következő gyepesedési sorrendnek felelnek meg (0 a kezdeti gyepes mezőket jelöli):

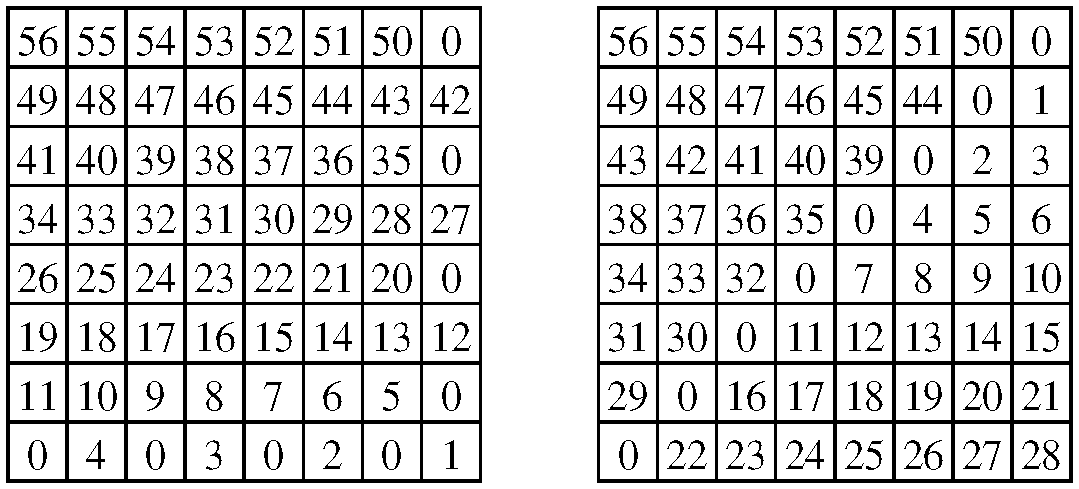
Gyakorlatilag a számokat 57-ből kivonva (a műveletek sorrendjét megfordítva) megkaptuk a gyepesedés egy lehetséges sorrendjét. A fentieknek megfelelően akkor a bástyalerakásnál kimaradó mezők lesznek a másik példában a kezdetben gyepesítendő mezők. Az pedig ismert állítás (ld. [1]), hogy a gyepesítési probléma esetén egy 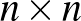$n\times n$ -es táblán legalább 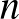$n$ mezőt kell gyepesíteni, hogy elterjedjen a gyep. Ennek a hivatkozásban is leírt bizonyítása a következő. Vegyük a kezdetben gyepesített mezők kerületét. Amikor terjed a gyep, akkor egy új gyepes mező legalább két oldala fog érintkezni a régebbi gyepes mezők oldalaival, úgyhogy azok nem lesznek a gyepes terület kerületén a továbbiakban. Másrészt az új gyepes mező nem gyepes szomszédaival közös oldalai bekerülnek a kerületbe. Ez alapján a gyepes terület kerülete nem nőhet. Ha az 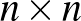$n\times n$ -es tábla minden mezője gyepes lesz a végén, akkor annak kerülete 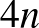$4n$ , így kezdetben is legalább 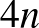$4n$ -nek kell lennie a kerületnek, tehát legalább 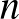$n$ mezőnek gyepesnek kell lennie, és lehet ilyen konfigurációt találni. Visszatérve az eredeti problémára ez azt jelenti, hogy a bástyalerakások végén még legalább 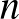$n$ üres mezőnek lennie kell, vagyis a 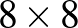$8\times 8$ -as tábla esetén legfeljebb 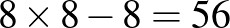$8\times 8-8=56$ bástya helyezhető el, és ez is megvalósítható.

Érdekes kérdés lehet, hogy hányféleképpen rakhatja le Marci a bástyákat úgy, hogy végül 56 bástya legyen a táblán. Igazából két lehetséges értelmezése van ennek a kérdésnek is: hány bástya végállás lehetséges, illetve hogy ha a lerakás sorrendje is számít, akkor azokból hány van.

Az első lehetséges értelmezése a kérdésnek (hogy t.i. hány különböző bástya végállás lehetséges) elérhetőnek tűnik: 64 mezőből 8 lesz üres, ilyenből 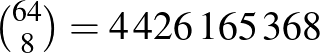$\binom{64}{8}=4\,426\,165\,368$ eset van. A gyepes példával való összekötésből tudjuk, hogy ezek az üres mezők nem lehetnek oldalszomszédosak, hiszen akkor a kerületük nem adná ki a gyepes példa végállásának 32-es kerületét, ez tovább csökkenti a lehetséges elhelyezések számát (abból már „csak” 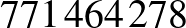$771\,464\,278$ darab van). Erre már írhatunk egy olyan programot, ami különösebb optimalizálás nélkül is végigellenőrzi ezeket kevesebb, mint 10 perc alatt. Eszerint 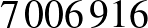$7\,006\,916$ bástya végállás lehetséges. Csak a kíváncsiság kedvéért kiszámoltattam kisebb táblákra is a lehetséges bástyaelhelyezések számát, és kikerestem megvizsgálandó esetek számát és az eredmények sorozatát is az On-Line Encyclopedia of Integer Sequences oldalon, és mindkettőt megtaláltam (https://oeis.org/A201511, https://oeis.org/A146971).

Ha a lerakás sorrendje is számít, akkor nyilván sokkal több esetet kell végignézetnünk a programmal, becsüljük meg, hogy mennyit. Induljunk ki a fenti második megoldásból, amikor a mellékátlóban nincsenek bástyák. Ebben az esetben a mellékátló feletti és a mellékátló alatti bástyák egymástól függetlenül lerakhatóak, így ha csak azt nézzük, hogy minden lépésben kiválaszthatjuk, hogy melyik oldalt építjük tovább, már akkor $\binom{56}{28}\approx 7,65\cdot 10^{15}$ lehetőségünk van, és ez már túl sok. De akár egy még nagyobb alsó becslést is mondhatunk. A mellékátló felett és alatt is alkalmazhatjuk a következő lerakási módszert: rakjuk le a sarokba az első bástyát, a mellékátlóval párhuzamos vonalon levő, a sarokkal szomszédos 2 bástyát bármilyen sorrendben, ezután a mellékátlóval párhuzamos vonalon levő ezekkel szomszédos 3 bástyát bármilyen sorrendben, és így tovább. 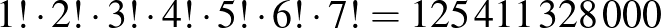Így a mellékátló alatt és felett is már legalább $1!\cdot 2!\cdot 3!\cdot 4!\cdot 5!\cdot 6!\cdot 7!=125\,411\,328\,000$ lerakási sorrendünk van, és ebből az egész táblára kapunk egy alsó becslést:

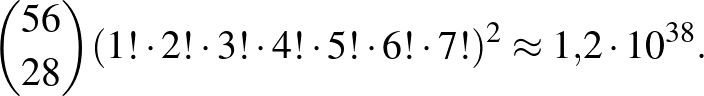
$\displaystyle \binom{56}{28}%\left(56\atop 28\right) (1!\cdot 2!\cdot 3!\cdot 4!\cdot 5!\cdot 6!\cdot 7!)^2\approx 1{,}2\cdot 10^{38}.$

Eszerint az összes ilyen sorrend kiszámolása egy mai számítógép számára messze túl van a lehetőségeken még erre az egyetlen végállásra is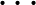 $\ldots$

Ez az alsó becslés elég pontosra sikeredett, mert a lehetséges lerakási sorrendek száma az átlós végállásra „csak” kb. 150 000-szer ekkora:

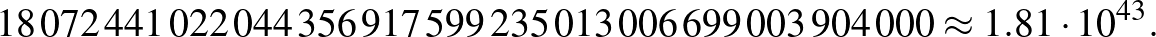
$\displaystyle 18\,072\,441\,022\,044\,356\,917\,599\,235\,013\,006\,699\,003\,904\,000\approx 1.81\cdot 10^{43}.$

(Csak ellenőrzésképpen: ezt a számot osztva az $\binom{56}{28}$ számmal és gyököt vonva belőle kapjuk meg, hogy az átló egyik oldalán hányféle sorrendben rakhatjuk le a bástyákat, és valóban egész számot kapunk: 48 608 795 688 960, ami tényleg nagyobb a 125 411 328 000-nél.)

Hogy honnan tudom ezt a számot? Annak ellenére, hogy megpróbáltam meggyőzni az olvasót (ahogy korábban saját magamat is 🙂) arról, hogy ez túl nagy szám ahhoz, hogy számítógéppel vizsgálható legyen a probléma, mégis vizsgálható. Ugyanis a cél nem az, hogy az összes lehetséges lerakási sorrendet meghatározzuk, hanem „csak” annyi, hogy ezek számát megkapjuk. Ezt a konkrét számot kevesebb, mint 7 másodperc alatt ki lehet számolni az alábbiakban ismertetett algoritmussal.

Nézzünk először egy egyszerű esetet, a 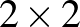$2\times 2$ -es „sakktáblát”. Itt 2 lehetséges végállás van: az átellenes sarokpárok adják meg ezeket. Könnyen végigkövethetjük egy irányított gráfon, hogy hányféleképpen lehet azokat kihozni:

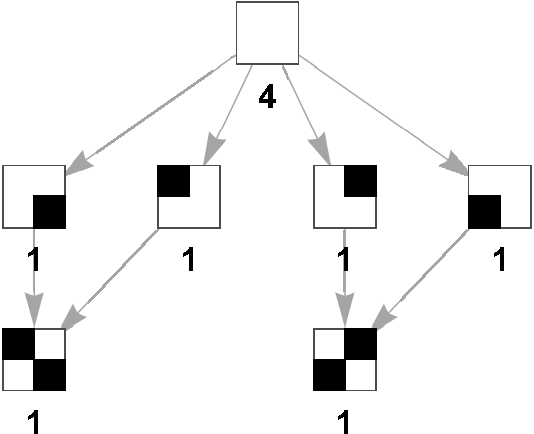
A gráf minden csúcsában egy állás van, az élek egy-egy bástya lerakásának felelnek meg. A lehetséges befejezések száma (a csúcs alatti szám) a belőle kiinduló élek végpontjainál levő csúcsok lehetséges befejezéseinek összege. A legalsó csúcsoknál (a végállásoknál) ez a szám nyilván 1, így alulról felfelé kitölthetjük a lehetséges befejezések számát. Az algoritmus (a technikai megvalósítás nehézségeitől eltekintve) így annyiból áll, hogy a már kiszámolt végállásokból határozzuk meg azokat a bástyaállásokat, amelyeken keresztül azok elérhetőek, rakjuk össze ezeket egy irányított gráfba, és számoljuk össze az esetek számát a fenti módon. Példaként legyen itt a 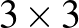$3\times 3$ -as táblához tartozó gráfnak az a része, amelyik a jobb felső sarkot tartalmazó kitöltéseket mutatja:

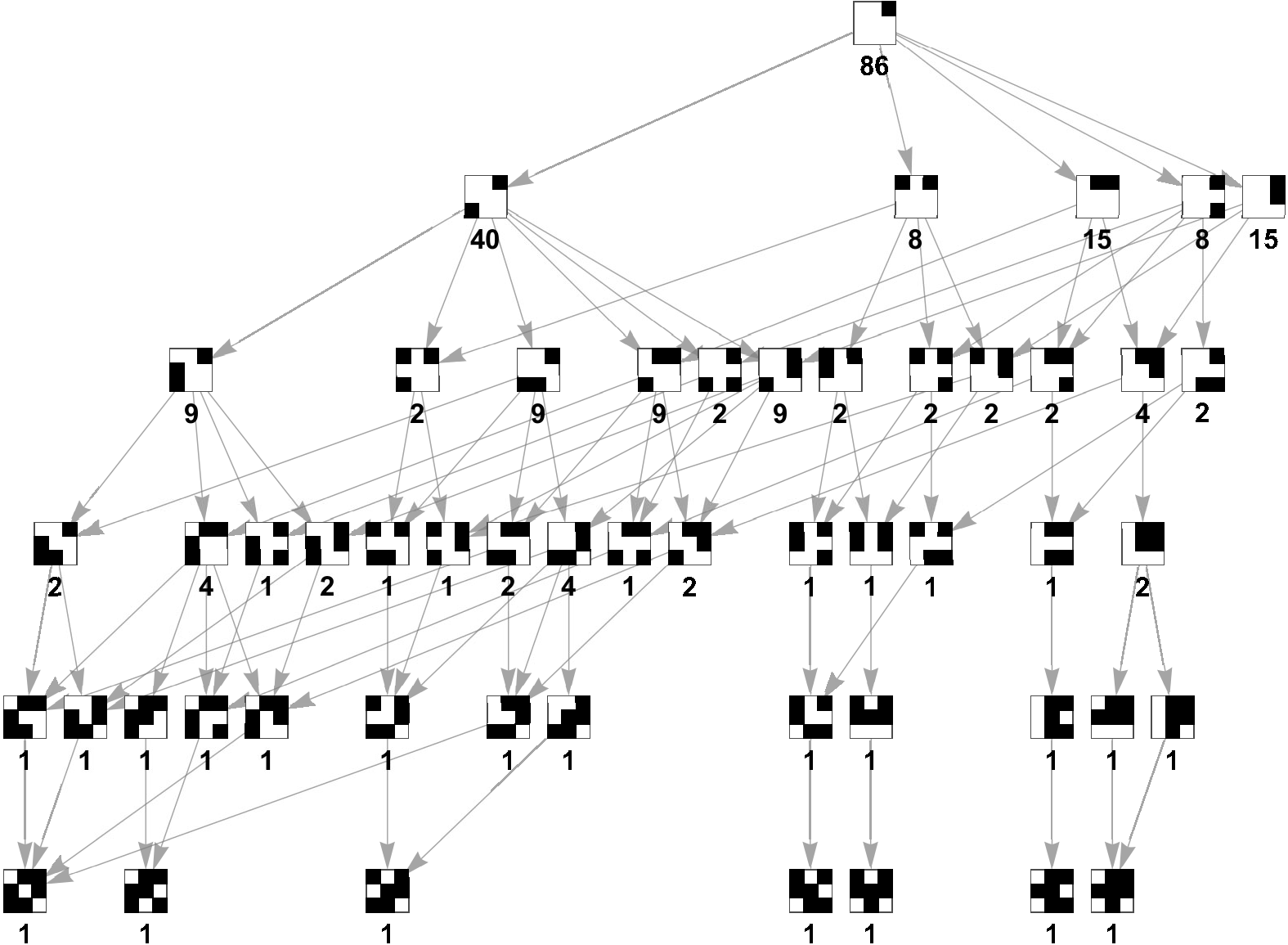
A fentiek alapján tudjuk, hogy mindenképpen valamelyik sarokban kell elkezdenünk a kitöltést, így a 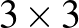$3\times 3$ -as esetben 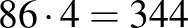$86\cdot 4=344$ az összes lehetséges kitöltések száma. Ugyanez az algoritmus (optimális módon megírva) működik a 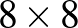$8\times 8$ -as tábla esetén is: 30.2 Gb memória felhasználással (a gráfunkban 870 540 024 csúcs és több mint 4.6 milliárd él lesz) 43 perc alatt megkapjuk az eredményt:

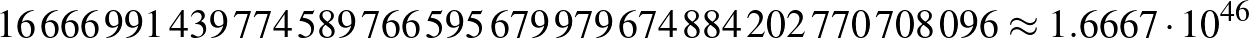
$\displaystyle 16\,666\,991\,439\,774\,589\,766\,595\,679\,979\,674\,884\,202\,770\,708\,096\approx 1.6667\cdot 10^{46}$

Ez nem kicsi szám. Ha a mai leggyorsabb szuperszámítógéppel próbálnánk az összes lehetséges lerakási sorrendet meghatározni, akkor az több, mint 30 000 milliárdszor milliárd évbe telne... 🙂

18. Gondoltam egy különböző jegyekből álló négyjegyű számra. A számnak az 5870, 1763, 9342, 4016 számok mindegyikével pontosan két közös számjegye van, és ezek a jegyek más helyeken állnak, mint a gondolt számban. Mi ez a szám?

Megoldás: Ez a Mastermind nevű játék egy állásának felel meg, ahol 4 színt kell kitalálni tippekkel, amelyekre a lehetséges válaszok, hogy egy szín helyes és a helyén van, vagy egy szín helyes, de nincs a helyén. Gyerekkoromban sokat játszottam ezzel a játékkal (még mindig megvan és unokaöcsikéimmel is játszottuk), így becsületbeli ügynek tekintettem, hogy ezt számítógép segítsége nélkül megoldjam (amúgy könnyű lenne programot írni rá).

A megadott négy számban az egyes számjegyek száma a következő:

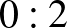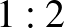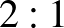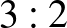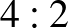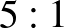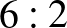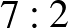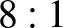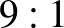$\displaystyle 0: 2$ db, $\displaystyle 1: 2$ db, $\displaystyle 2: 1$ db, $\displaystyle 3: 2$ db, $\displaystyle 4: 2$ db, $\displaystyle 5: 1$ db, $\displaystyle 6: 2$ db, $\displaystyle 7: 2$ db, $\displaystyle 8: 1$ db, $\displaystyle 9: 1$ db.

A négy számból összesen 8 helyes számjegynek kell összejönnie, így a négy különböző számjegy mindegyike pontosan kétszer kell előforduljon, hiszen ha egy olyan számjegy szerepelne a gondolt számban, ami a csak egyszer fordul elő a fenti négy számban, akkor kellene lennie olyan számjegynek is, ami legalább háromszor fordul elő, olyan pedig nincs. Így kizárhatjuk a 2, 5, 8, 9 számjegyeket. Ezeket (gondolatban) kihúzva az első és harmadik számból a 0, 3, 4, 7 számjegyek maradnak meg. A százas helyiértéken a számokban szerepel a 7, 3 és 0 számjegy, így ott csak a 4-es lehet. Az egyes helyiértéken szerepel a 0 és a 3, a 4-est már elhelyeztük, úgyhogy oda a 7-est kell írnunk. Mivel a gondol szám négyjegyű, az első számjegye nem lehet a 0, oda kerül a 3-as és a tízesek helyére a 0. A gondolt szám tehát a 3407.

De ha már emlegettem a programozást: érdekes feladat egy olyan programot írni a Mastermind játékra, ami az ember által kigondolt számot (színkombinációt) minél kevesebb tippel kitalálja. Egy adott állásban még lesznek lehetséges megoldások, ezek számát próbáljuk csökkenteni. A programban több stratégia is elképzelhető:

1. Olyat tippeljünk, ami az arra adható válaszok alapján a legrosszabb esetben is minél több lehetséges megoldást kizár. Ez az okos (és „ellenséges”) emberi ellenfelek esetén jó: ha az ember a kitalált számát mindig úgy változtatja meg, hogy az az eddig általa adott információknak megfeleljen, de minél több legyen a még lehetséges megoldások száma.

2. Olyat tippeljünk, ami az arra adható válaszok alapján a legjobb esetben minél több lehetséges megoldást kizár. Ez az okos (és „jóindulatú”) emberi ellenfelek esetén jó: ha az ember a kitalált számát mindig úgy változtatja meg, hogy az eddig általa adott információknak megfeleljen, és minél kevesebb legyen a még lehetséges megoldások száma. Persze, ha ezt szó szerint vesszük, akkor a gép első tippjére azt kellene mondania az embernek, hogy az volt a helyes... 🙂

3. A legkiegyensúlyozottabb stratégia valószínűleg az, hogy olyat tippelünk, ami az arra adható válaszok alapján átlagban minél több lehetséges megoldást kizár. Ez a „fair” emberi játékosok esetén lesz hatékony, akik nem változtatgatják a kitalált számukat.

Érdekes dolog, hogy (bármelyik esetet is nézzük) nem az az elsődleges cél, hogy jót tippeljünk, hanem hogy kizárjuk a rosszakat. Az emberek többsége hajlamos az előbbire törekedni a játékban, márcsak azért is, mert az utóbbit végiggondolni sokkal bonyolultabb. Végül meg is írtam ezt a programot az 1. stratégiával [2], itt egy példa futtatás eredménye:

Figyeljük meg, hogy az ötödik lépésben már megvoltak a kódban levő számjegyek, a hatodik lépésben a gép mégsem azokat a számjegyeket használva tippelt: több esetet tudott kizárni egy „rosszabb” tippel.

Persze, a programmal meg lehet oldatni a feladatot is erre a linkre kattintva. Próbáljuk meg többször is újratölteni az oldalt. Ez megadja a feladat két lehetséges megoldását: a kódban lehet 0 az első számjegy, a feladatban nem, de ez utóbbit nem programoztam bele a programba. Az olvasónak egy kis gondolkodnivaló, hogy a Status változó értéke milyen módon írja le a feladat problémáját... 🙂

A program megírása után fedeztem fel Donald Knuth (A számítógép-programozás művészete című mű szerzője, a TEX tördelőszerkesztő rendszer megalkotója [ezt a cikket is TEX-ben írom]) egyik cikkét [3], amelyben az eredeti MasterMind játékot elemzi. Ebben az 1. stratégia alapján bizonyítja, hogy 6 szín és 4 hely esetén legfeljebb öt tippel kitalálható a titkos kombináció. Ehhez már 1977-ben (!) számítógépet használt, és már Ő is felfedezte, hogy nem feltétlenül egy lehetséges megoldást kell tippelni.

20. Lehetséges-e egy társaságban, hogy a jelenlévők közül mindenki 4 másikat ismer, és a társaság bármely két egymást nem ismerő tagjának a többiek között pontosan 2 közös ismerőse van? (Az ismeretségek kölcsönösek, és a társaságnak vannak tagjai.)

Megoldás: Igen, egy 5 tagú társaságban, ha mindenki ismer mindenkit, akkor az megfelel a feladat feltételeinek.

Persze, túl egyszerű lenne ennyivel elintézni a dolgot, hiszen akkor a feladat második tagmondata egy üreshalmazra vonatkozik. Szokás szerint programot írtam rá, és van megoldás 8 és 9 tagú társaságra is. Ezekben a szomszédsági mátrixokban az x jelöli, hogy ki ismer kit, és gráfizomorfiától eltekintve ez az összes lehetséges megoldás:

Nyilván 5-nél kevesebb ember nem lehet a társaságban, 5 ember esetén pedig mindenkinek ismernie kell mindenkit. Az könnyen belátható, hogy 6 és 7 tagú társaság nem felelhet meg a feltételnek: ekkor ugyanis lesznek olyan emberpárok, akik nem ismerik egymást, viszont „túl sok” embert ismernek, így a közös ismerőseik száma legalább 4, illetve 3 lesz.

Érdekes a mintamegoldásban a 9 emberre vonatkozó konstrukció, a fenti szomszédsági mátrix persze megfelel annak. De emiatt elgondolkodtam a 8 emberes megoldásokon, hogy azoknak van-e valami „geometriai” jelentése. A középső szomszédsági mátrixra viszonylag könnyen találtam jelentést: egy szabályos nyolcszögben a szomszédok és a második szomszédok legyenek ismerősök (ez amúgy is teljesen „normális”, az ember a legközelebbi szomszédait ismeri ☺). Az elsőre ez már nehezebb volt, de végülis sikerült a Wolfram Mathematica segítségével: egy kocka élei, és két egymással szemközti lapjának lapátlói adják meg az ismeretséget. Ezek a gráfok felelnek meg a fenti szomszédsági mátrixoknak:

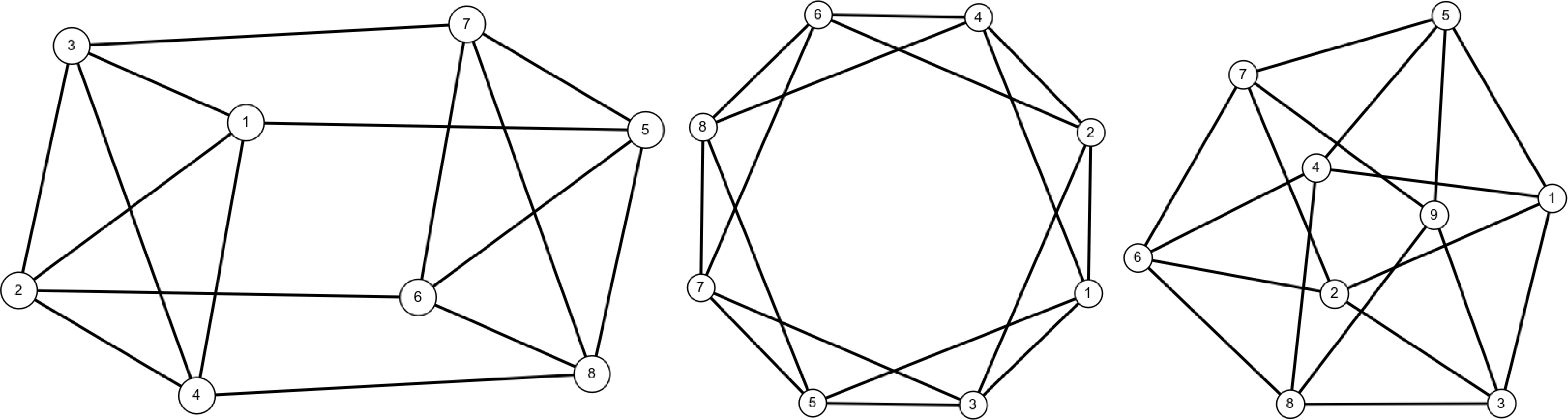
A programom nem talált megoldást 10-17 emberre (nagyobb számra már túl sok ideig futott volna). Úgyhogy az a sejtés, hogy 10-nél több ember esetén nem lehetséges a feladat állítása. Számoljunk egy kicsit. 2 egymásnak ismeretlen ember között van 2 darab kettő hosszú út. Így ha 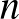$n$ ember van a társaságban, akkor mindenkinek 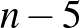$n-5$ ember lesz ismeretlen, vagyis az ismeretlen párok száma 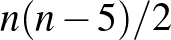$n(n-5)/2$ , és a köztük lévő különböző kettő hosszú utak száma 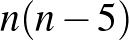$n(n-5)$ . A kettő hosszú utak számát úgy is meghatározhatjuk, hogy ha egy adott ember ismerősei nem ismerik egymást, akkor 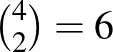$\binom{4}{2}=6$ darab kettő hosszú út keletkezik, amelyiken az adott ember „középen” van. Ezek a kettő hosszú utak különbözőek, hiszen különbözőek a középen álló emberek, így az összes kettő hosszú utak száma 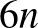$6n$ . 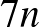Eszerint $n\geq 12$ esetén legalább $7n$ darab kettő hosszú út kellene, de csak 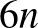$6n$ darab van. Mivel 10-re és 11-re programmal ellenőriztük, hogy nincs megfelelő ismeretség, 12-től pedig beláttuk, hogy nem is lehetséges ilyen ismeretség, ezért igaz, hogy 10-nél több emberre nincs megoldása a feladatnak. A fentiek alapján ezek szerint csak 4 lényegesen különböző megoldás van: 5 és 9 emberre 1-1, 8 emberre 2.

Érdemes megjegyezni, hogy a fenti bizonyítás alapján véges sok megoldás van akkor is, ha egy 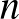$n$ tagú társaságban mindekinek legfeljebb 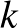$k$ ismerőse van, és bármelyik két ismeretlennek van legalább 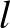$l$ közös ismerőse ( 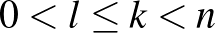$0<l\leq k<n$ ). 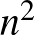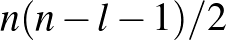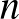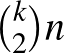Ugyanis az ismeretlen párok száma az ilyen esetekben $n^2$ nagyságrendű lesz: ( $n(n-l-1)/2$ ), míg a közös ismerősök alapján az ismeretlen párokat összekötő kettő hosszú utak száma $n$ -nel arányos: ( $\binom{k}{2}n$ ).

Makay Géza
Szegedi Tudományegyetem, Bolyai Intézet

Ezt a kutatást a TKP2021-NVA-09 projekt támogatta. A TKP2021-NVA-09 számú projekt a Magyar Innovációs és Technológiai Minisztérium támogatásával valósult meg a Nemzeti Kutatási, Fejlesztési és Innovációs Alapból, a TKP2021-NVA támogatási konstrukció keretében.