A 3. forduló feladataira 19 beküldőtől 107 jó válasz érkezett.
A táblázat mutatja, hogy a legeredményesebb beküldők mely feladatokra adtak helyes választ. (Vannak, akik a saját nevükkel szerepelnek, és vannak, akik más nevet választottak maguknak.)
| A feladat sorszáma | 15. | 16. | 17. | 18. | 19. | 20. | 21. |
| Orangestripes | x | x | x | x | x | x | x |
| D & 2d | x | x | x | x | x | x | x |
| Dombi Péter | x | x | x | x | x | x | x |
| Keresztvölgyi József | x | x | x | x | x | x | x |
| Makay Géza | x | x | x | x | x | x | |
| vukung | x | x | x | x | x | x | |
| Udvari Tibor | x | x | x | x | x | x | |
| Szemerédi Ferenc | x | x | x | x | x | x | |
| Emil | x | x | x | x | x | x | |
| Belzebub | x | x | x | x | x | x | |
| Jankó Zsuzsanna | x | x | x | x | x | x | |
| Berkó Erzsébet | x | x | x | x | x | x | |
| Kovach M. László | x | x | x | x | x | ||
| Megérek egy Petákot | x | x | x | x | x | ||
| Danka Emma (diák) | x | x | x | x | x | ||
| Kengyelfutó Einstein (diák) | x | x | x | x | x | ||
| Vaszary Krisztián (diák) | x | x | x | x | x |
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak. A jutalmazottak, „D & 2d” a Polygon Jegyzettárból (Csákány Béla: Diszkrét matematikai játékok), „Orangestripes” pedig a Bolyai Társulat és a Springer közös kiadványaiból (Volume 28: Building Bridges II., Szerkesztette: Bárány Imre, Katona Gyula, Sali Attila) választott könyvet.
A feladatok megoldása (további megjegyzésekkel)
15. Az 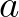 ,
, 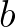 ,
,  egész számokra az
egész számokra az 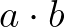 és
és 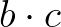 számok négyzetszámok.
számok négyzetszámok.
Igaz-e, hogy ekkor 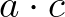 is egy egész szám négyzete?
is egy egész szám négyzete?
Megoldás. A válasz: Hamis.
Egy példa erre: 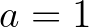 ,
, 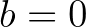 ,
, 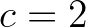 . Ekkor
. Ekkor 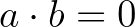 és
és 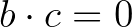 (és a 0 négyzetszám!), de
(és a 0 négyzetszám!), de 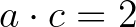 .
.
Az állítás igaz, ha a nulla nem szerepelhet a számok között.
Ha az 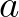 ,
, 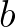 ,
,  pozitív egész számokra az
pozitív egész számokra az 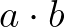 és
és 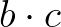 számok négyzetszámok, akkor
számok négyzetszámok, akkor 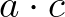 is egy egész szám négyzete.
is egy egész szám négyzete.
Ez igaz, kétféleképpen is indokoljuk.
a) Legyen 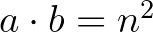 és
és 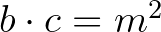 , ekkor
, ekkor 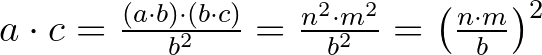 . A feltételek miatt
. A feltételek miatt  osztója
osztója 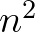 -nek és
-nek és 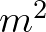 -nek, tehát
-nek, tehát 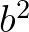 osztója
osztója 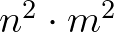 -nek, azaz
-nek, azaz 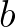 osztója
osztója 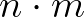 -nek. Tehát
-nek. Tehát 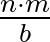 egész szám. Ezzel igazoltuk, hogy
egész szám. Ezzel igazoltuk, hogy 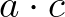 négyzetszám. (Az átalakításokban felhasználtuk, hogy
négyzetszám. (Az átalakításokban felhasználtuk, hogy 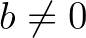 , ezért oszthatunk vele.)
, ezért oszthatunk vele.)
b) Nézhetjük az 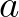 ,
,  ,
,  számok prímtényezőit. Ha az
számok prímtényezőit. Ha az  és
és 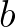 számoknak
számoknak 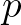 közös prímtényezője, és
közös prímtényezője, és 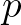 páratlan kitevővel szerepel az
páratlan kitevővel szerepel az 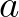 szám prímtényezős felbontásában, akkor páratlan kitevője lesz a
szám prímtényezős felbontásában, akkor páratlan kitevője lesz a 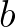 szám prímtényezős alakjában is, hiszen
szám prímtényezős alakjában is, hiszen 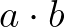 négyzetszám. Mivel
négyzetszám. Mivel 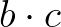 is négyzetszám, és a
is négyzetszám, és a 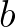 szám prímtényezős alakjában
szám prímtényezős alakjában 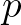 páratlan kitevővel szerepel, emiatt a
páratlan kitevővel szerepel, emiatt a  szám prímtényezős felbontásában is páratlan kitevője lesz. Ekkor az
szám prímtényezős felbontásában is páratlan kitevője lesz. Ekkor az 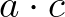 szorzatban ennek a prímnek a kitevője két páratlan szám összege, páros szám lesz. Az
szorzatban ennek a prímnek a kitevője két páratlan szám összege, páros szám lesz. Az 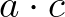 szorzatban a prímkitevőket nézve mindegyik páros, így a szorzat négyzetszám. (A 0-nak nincs prímtényezős alakja.)
szorzatban a prímkitevőket nézve mindegyik páros, így a szorzat négyzetszám. (A 0-nak nincs prímtényezős alakja.)
Megjegyzés. A nulla zavart okozott, emiatt sokan hibás választ adtak. A nullát van, aki természetes számnak nevezi, és van aki nem, mindkét gyakorlat indokolható, érthető. Négyzetszám esetén nincs megfontolható ok, hogy a nullát kizárjuk. Persze, ha négyzetszámokról beszélünk, a nullát ritkán emlegetjük1.
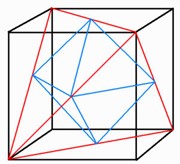
16. Adott egy négyzetalapú gúla és egy tetraéder. Ezeknek minden éle 1 egység hosszú. A tetraédert a gúla egyik oldallapjára illesztettük úgy, hogy az illeszkedő lapok fedik egymást. Hány oldallapja van az így kapott testnek?
1. megoldás. A válasz: 5.
Az ábra szerint helyezzünk a gúla mellé egy másik, vele egybevágó gúlát. A két gúla között látunk egy tetraédert, amelynek minden éle 1 egység. A két gúlából és a tetraéderből álló testnek 5 lapja van.
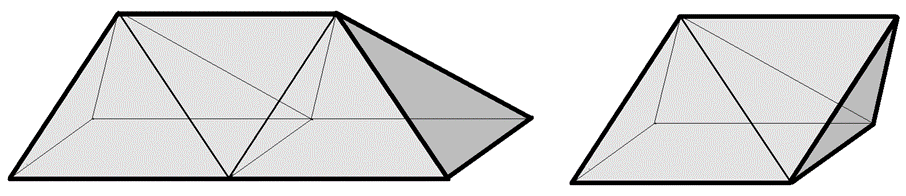
A most kapott testből vegyük el az egyik gúlát, és megkapjuk azt a testet, amiről a feladat beszél. Ennek a testnek 5 lapja van.
2. megoldás. (Dombi Péter megoldása.) A testnek öt oldala van. Az egyesítés egy háromszög alapú ferde hasáb lesz, a palást egyik oldallapja négyzet, a másik kettő pedig 60 fokos rombusz.
Egyszerű belátni, hogy a tetraéder és a gúla megfelelő oldallapjai a gúla oldaléleinél egy síkba esnek. Képzeljük a gúlát egy kocka oldalközéppontjai által meghatározott fél oktaédernek, ekkor a hozzá illesztett szabályos tetraédert a kocka egyik csúcsa és az ehhez illeszkedő 3 lapközéppont alkotja, viszont a gúla oldallapja is, és ennek a „kis” tetraédernek a megfelelő oldallapja is a kockacsúcsok által meghatározott „nagy” tetraéder megfelelő lapsíkjában fekszenek.
17. Marci bástyákat rak egy üres sakktáblára. Akkor helyezhet el egy bástyát egy üres mezőre, ha annak legalább két oldalszomszédja üres. Legfeljebb hány bástyát helyezhet a táblára Marci?
Megoldás. A válasz: 56.
A tábla mezőit jelöljük egy-egy ponttal, és ha két mező szomszédos, akkor a két pontot kössük össze szakasszal. Így a 64 pont között 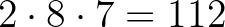 szakaszt rajzolunk.
szakaszt rajzolunk.

Ha elfoglalunk egy mezőt, akkor szüntessük meg az innen induló szakaszokat. Ilyenkor legalább két szakaszt törlünk. Egy újabb bástyát csak olyan mezőre tehetünk, ahonnan legalább 2 szakasz indul.
Ezért legfeljebb 56 bábut tehetünk fel, hiszen 57 bábu elhelyezésével legalább 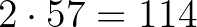 szakaszt szüntetnénk meg.
szakaszt szüntetnénk meg.
Elhelyezhetünk 56 bábut, ezt látjuk az ábrán. A táblán a számok mutatják a felhelyezés sorrendjét.

Megjegyzés. A beküldött megoldások alapján három kiegészítés következik.
Udvari Tibor egy másik elhelyezést mutatott: 56 bástya elhelyezhető. A bal felső sarokból kiindulva soronként helyezzünk el annyi bástyát, amennyit csak lehet. Így az első sorban 7, a másodikban 8, majd megint 7, 8, 7, 8, 7 tehető a táblára. Az utolsó sorban a másodiktól kezdve 4 tehető le, ez együtt 56. (Más módon is letehető 56 bástya.)
Dombi Péter bizonyítása arra, hogy 56-nál több több bástyát sehogy sem lehet lerakni, nem könnyű, de nagyon rövid. Az üres területrész kerülete egy-egy bástya elhelyezésénél legalább 2 éllel nő (ti. ott, ahol üres szomszédokkal érintkezik), és legfeljebb kettővel csökken (ahol foglaltakkal érintkezik), tehát összességében nem csökken. Kiinduláskor 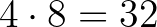 volt a kerülete, de ez véghelyzetben, 7 üres mezővel csak
volt a kerülete, de ez véghelyzetben, 7 üres mezővel csak 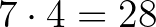 , vagy még kevesebb lenne. (Tehát az üres mezők száma legalább 8.)2
, vagy még kevesebb lenne. (Tehát az üres mezők száma legalább 8.)2
Adható teljes indukciós bizonyítás is arra, hogy 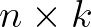 -as táblán legalább
-as táblán legalább 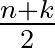 mező üresen marad.
mező üresen marad.
A feladat eléggé közismert fordított szemléletben, amikor néhány „gazos” mező kezd terjedni az egynél több gazos szomszéddal rendelkező mezőkre (lásd pl. KöMaL, F.3220., 1998. március)3.
Megemlíthető, hogy bárhogyan rakosgatjuk – a szabályt betartva – a bástyákat a 8 x 8-as táblára, 32 darabot mindenképpen el tudunk helyezni. Ugyanis 31 bástya után még biztosan található olyan 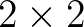 -es rész, ahova a cellaszám felénél kevesebb, azaz legfeljebb 1 figura jutott.
-es rész, ahova a cellaszám felénél kevesebb, azaz legfeljebb 1 figura jutott.
Végül Makay Géza még tovább gondolta a feladatot: vajon hányféleképpen rakhatja le Marci a bástyákat úgy, hogy végül 56 bástya legyen a táblán? Erről, továbbá a következő, 18. és 20. feladatokhoz fűzött kiegészítéseiről a Mastermind, bástyák és ismerősök című cikkünkben olvashatnak.
18. Gondoltam egy különböző jegyekből álló négyjegyű számra. A számnak az 5870, 1763, 9342, 4016 számok mindegyikével pontosan két közös számjegye van, és ezek a jegyek más helyeken állnak, mint a gondolt számban. Mi ez a szám?
Megoldás. A válasz: 3407.
A négy számban összesen 8 számjegyet találtunk el.
Mivel nincs olyan számjegy, amely háromszor ismétlődne a számokban, ezért gondolt szám mindegyik jegyét kétszer találtuk el.
Az adott négy számban kétszer szereplő számjegyek 0, 1, 3, 4, 6, 7. Ezek között vannak a gondolt szám számjegyei.
Tehát a 2, 5, 8 és 9 jegyek egyike sincs a gondolt számban.
Ezért 5870-ben eltaláltuk a 0 és 7 jegyeket.
A 9342 számban 3 és 4 talált.
Már tudjuk, hogy a gondolt szám jegyei 0, 3, 4 és 7.
Hol állhatnak ezek a számjegyek?
A 0 az 1. vagy 3. helyen, de 0 nem állhat az első helyen, tehát a 3. lesz.
A 3 is az 1. vagy 3. helyen állhat, a 3. helyen 0 áll, így marad az 1. hely.
A 7 az 1. vagy 4. helyen lehet, foglalt az 1. hely, így a 4. helyen áll.
A 4-nek marad a 2. hely.
A gondolt szám: 3407.
19. A síkon felvettünk 8 pontot úgy, hogy nincs közte három, amely egy egyenesre esne. Az egyik pont piros, a többi kék. Nevezzünk egy kék csúcsú háromszöget pirosnak, ha a belsejében ott van a piros pont. Lehetséges-e, hogy a háromszögeknek legalább a fele piros?
Megjegyzés. A feladat kérdése eredetileg így szólt volna: Lehetséges-e, hogy a kék csúcsú háromszögeknek legalább a fele piros? A kitűzött feladat kérdésére és erre a kérdésre is ugyanaz a válasz: Nem lehet.
Mindkét kérdésre adunk megoldást:
1. megoldás. Az összes háromszög felénél kevesebb a pirosak száma.
A 8 pontból hármat-hármat választva 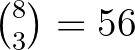 háromszöget kapunk. A kék csúcsú háromszögek száma
háromszöget kapunk. A kék csúcsú háromszögek száma 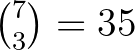 . Nevezzünk egy háromszöget kéknek, ha a csúcsai kék pontok és a háromszög nem tartalmazza a piros pontot. Megmutatjuk, hogy van legalább 8 kék háromszög, ezért a piros háromszögek száma legfeljebb
. Nevezzünk egy háromszöget kéknek, ha a csúcsai kék pontok és a háromszög nem tartalmazza a piros pontot. Megmutatjuk, hogy van legalább 8 kék háromszög, ezért a piros háromszögek száma legfeljebb 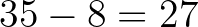 lehet, és ez kevesebb 28-nál, az összes lehetőség felénél.
lehet, és ez kevesebb 28-nál, az összes lehetőség felénél.
Vegyünk fel egy olyan egyenest, amely illeszkedik a piros pontra, és nincs rajta kék pont. Az egyenes egyik oldalán a 7 kék pontból legalább 4 pont fekszik. Nézzük ezt a 4 pontot. Egyet-egyet kihagyva, a megmaradó három pont kék háromszöget alkot. Ez eddig 4 kék háromszög.
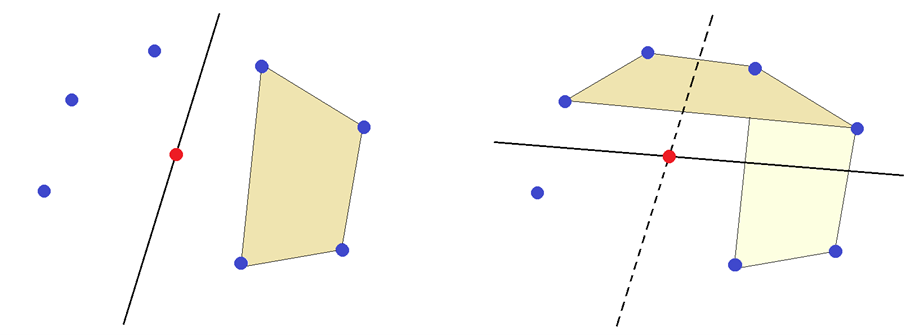
Van még 3 kék pont, amelyeket nem vizsgáltunk. Vegyünk fel egy második egyenest a piros ponton keresztül úgy, hogy ne legyen rajta kék pont, és az egyenes „felezze el” az előbb kiszemelt 4 pontot, azaz a 4 pontból 2 pont az egyenes egyik oldalán, 2 pont a másik oldalán legyen. Az egyenes egyik oldalán a 3 kék pontból legalább 2 fekszik. Így a második egyenes egyik oldalán 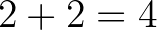 olyan pont fekszik, amelynek az előbbi 4 ponttal csak két közös pontja van. A most választott 4 pont meghatároz 4 újabb kék háromszöget.
olyan pont fekszik, amelynek az előbbi 4 ponttal csak két közös pontja van. A most választott 4 pont meghatároz 4 újabb kék háromszöget.
2. megoldás. A kék csúcsú háromszögek felénél kevesebb a pirosak száma.
Válasszunk 4 kék pontot, az 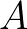 ,
, 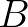 ,
, 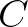 ,
, 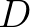 pontokat. Ha
pontokat. Ha  konvex négyszög, akkor ezt egy átlója két háromszögre vágja, és csak az egyikben lehet piros pont. Ekkor az
konvex négyszög, akkor ezt egy átlója két háromszögre vágja, és csak az egyikben lehet piros pont. Ekkor az  ,
,  ,
, 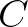 ,
, 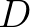 pontnégyesből választható 4 háromszög közül legfeljebb 2 háromszög piros.
pontnégyesből választható 4 háromszög közül legfeljebb 2 háromszög piros.
Ha az 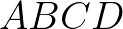 négyszög konkáv, akkor is legfeljebb 2 háromszög piros az
négyszög konkáv, akkor is legfeljebb 2 háromszög piros az 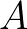 ,
, 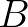 ,
, 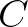 ,
, 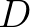 pontnégyesből választható 4 háromszög közül.
pontnégyesből választható 4 háromszög közül.
Tehát 4 kék pont esetén legfeljebb 2 olyan piros háromszög van, amelynek csúcsait ezen pontok közül választjuk.
Így számlálva legfeljebb  piros háromszöget számolunk, persze egy-egy piros háromszöget többször is megszámolunk. Egy piros háromszög három kék csúcsához a negyedik kék csúcsot
piros háromszöget számolunk, persze egy-egy piros háromszöget többször is megszámolunk. Egy piros háromszög három kék csúcsához a negyedik kék csúcsot 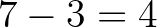 pont közül választhatjuk, azaz a számlálás során egy piros háromszöget 4-szer számolunk meg.
pont közül választhatjuk, azaz a számlálás során egy piros háromszöget 4-szer számolunk meg.
Ezért a piros háromszögek száma legfeljebb
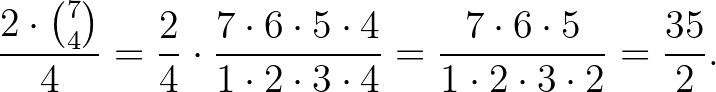
Legfeljebb ![$\left[\frac{35}{2}\right]=17$](/images/stories/latexuj/2024-02/2024-02-megoldasokahettusaharmadikfordulojahoz/img46.png) piros háromszög van, míg a kék csúcsú háromszögek száma
piros háromszög van, míg a kék csúcsú háromszögek száma 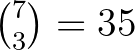 . Ezért nem lehet a háromszögeknek legalább a fele piros.
. Ezért nem lehet a háromszögeknek legalább a fele piros.
3. megoldás. (Dombi Péter megoldása.) A 35 háromszögből legfeljebb 14-ben lehet a piros pont.
Válasszuk a piros pontot origónak, a kék pontokba mutató vektorok legyenek 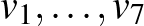 . Három végpont háromszöge pontosan akkor tartalmazza az origót, ha a három vektor által generált kúp az egész sík, vagy másképp, ha a belőlük képzett
. Három végpont háromszöge pontosan akkor tartalmazza az origót, ha a három vektor által generált kúp az egész sík, vagy másképp, ha a belőlük képzett 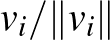 egységvektorok végpontjai az egységkörön hegyesszögű háromszöget alkotnak. Elég tehát megbecsülni, hogy az egységkörön 7 általános helyzetű
egységvektorok végpontjai az egységkörön hegyesszögű háromszöget alkotnak. Elég tehát megbecsülni, hogy az egységkörön 7 általános helyzetű 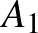 ,
,  ,
,  pont legalább hány tompaszögű háromszöget határozhat meg (derékszögű nem léphet fel).
pont legalább hány tompaszögű háromszöget határozhat meg (derékszögű nem léphet fel).
Rögzítve pl. az 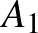 pontot, olyan tompaszögű háromszöget, amelynek egyik hegyesszöge
pontot, olyan tompaszögű háromszöget, amelynek egyik hegyesszöge 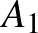 -nél van, akkor és csak akkor kapunk, ha a háromszög másik két csúcsa az
-nél van, akkor és csak akkor kapunk, ha a háromszög másik két csúcsa az 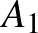 végpontú átmérő azonos oldalára esik. Ilyenből a legkevesebb (6) akkor áll elő, ha a többi hat pontból 3-3 pont esik egy-egy félkörre. Ugyanezt elmondva
végpontú átmérő azonos oldalára esik. Ilyenből a legkevesebb (6) akkor áll elő, ha a többi hat pontból 3-3 pont esik egy-egy félkörre. Ugyanezt elmondva 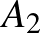 ,
, 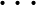 ,
, 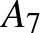 -re, legalább
-re, legalább 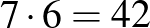 tompaszögű háromszöget kapunk, viszont minden tompaszögű háromszöget kétszer is megszámoltunk, mert két hegyesszöge van, ezért a helyes becslés ennek a fele:
tompaszögű háromszöget kapunk, viszont minden tompaszögű háromszöget kétszer is megszámoltunk, mert két hegyesszöge van, ezért a helyes becslés ennek a fele: 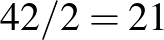 . Legalább 21 tompaszögű háromszög mellett legfeljebb
. Legalább 21 tompaszögű háromszög mellett legfeljebb 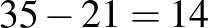 hegyesszögű háromszög lehet, és így a piros pontot tartalmazó háromszögből is legfeljebb ennyi lehet.
hegyesszögű háromszög lehet, és így a piros pontot tartalmazó háromszögből is legfeljebb ennyi lehet.
Általános esetben, az egységkörön felvett 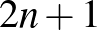 pont esetén, bármelyik ponthoz a rajta átmenő átmérő két félkörén legalább
pont esetén, bármelyik ponthoz a rajta átmenő átmérő két félkörén legalább 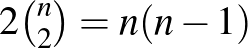 tompaszögű háromszög illeszkedik (ha a maradék
tompaszögű háromszög illeszkedik (ha a maradék 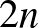 pontot nem felezi az átmérő, akkor még több). Így a tompaszögű háromszögek száma legalább
pontot nem felezi az átmérő, akkor még több). Így a tompaszögű háromszögek száma legalább 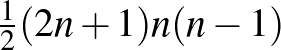 , ami közelítőleg
, ami közelítőleg 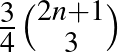 , vagyis nagy
, vagyis nagy 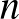 -ekre a háromszögeknek közelítőleg
-ekre a háromszögeknek közelítőleg 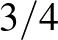 része biztosan tompaszögű, vagy ami ugyanaz, a feladatbeli háromszögeknek jó közelítéssel legfeljebb a negyed része tartalmazhatja a piros pontot.
része biztosan tompaszögű, vagy ami ugyanaz, a feladatbeli háromszögeknek jó közelítéssel legfeljebb a negyed része tartalmazhatja a piros pontot.
20. Lehetséges-e egy társaságban, hogy a jelenlévők közül mindenki 4 másikat ismer, és a társaság bármely két egymást nem ismerő tagjának a többiek között pontosan 2 közös ismerőse van? (Az ismeretségek kölcsönösek, és a társaságnak vannak tagjai.)
Megjegyzés. Pontatlan a feladat, nehezebb akart lenni. A nehezebb változathoz ez a fogalmazás kell: Az ismeretségek kölcsönösek, és a társaságnak vannak egymást nem ismerő tagjai.
A kitűzött feladat kérdésére és erre a kérdésre is ugyanaz a válasz: Lehetséges.
Belzebub írja: Lehetséges, több módon is, pl ha a társaság 5 tagú, és mindenki ismer mindenkit, azaz mindenkinek 4 ismerőse van, továbbá az egymást nem ismerők halmaza üres, ami miatt a második feltétel is teljesül.
Szebb megoldásnak tartom a 8 tagú társaságot. Ültessünk le 8 egymást nem ismerő embert egy kerek asztal köré. Mindenki megismeri a közvetlen és az amellett ülő 1-1 embert (azaz ismeri a legfeljebb 2. szomszédját). Az így kialakuló ismeretségi rendszer is megfelel a kért feltételnek. (Mindenkinek 3 ember marad idegen, a vele szemben ülő, és annak két szomszédja, a szemben ülővel a közös ismerősök a tőlük 2 távolságra ülők, annak szomszédaival pedig a köztük ülő két ember.)
Udvari Tibor konstrukciója 8 fős társaságra: a 8 fő egy kocka 8 csúcsa, az ismeretségek közöttük a kocka élei, és két szemközti lapon a lapátlók.
Megoldás.
Például legyen a társaság 9 fős. A táblázatban lévő 9 kör szemlélteti őket, és mindenki a vele egy sorban, valamint a vele egy oszlopban lévőket ismeri, a többieket nem. ( ismerősei 1, 2, 3, 4;
ismerősei 1, 2, 3, 4;  és
és  közös ismerősei 1 és 2.)
közös ismerősei 1 és 2.)
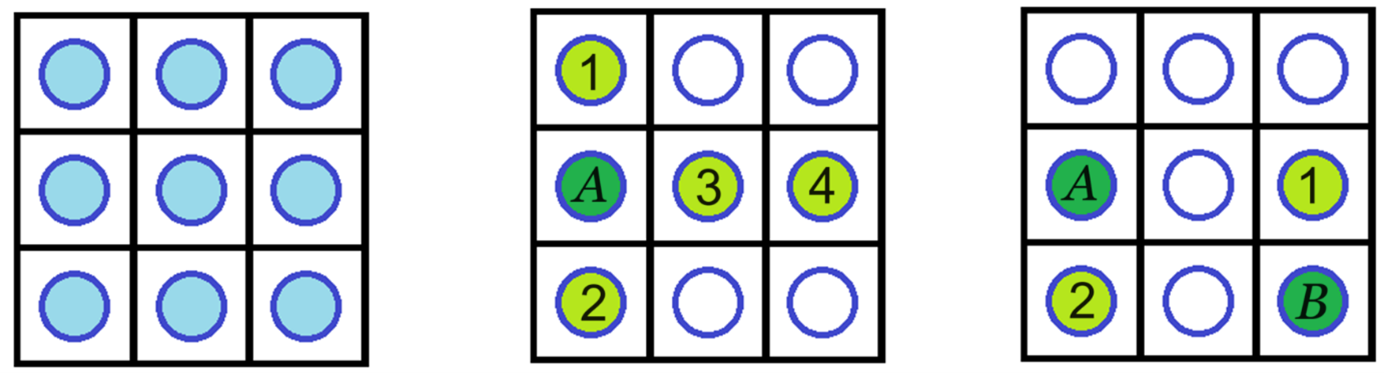
Ilyen ismeretségi kapcsolatok esetén teljesül a feladat elvárása.
Makay Géza: Mastermind, bástyák és ismerősök c. cikke tisztázza, hogy a társaság létszáma 5, 8 vagy 9. Nyolc fő esetén két konstrukció van, 5 és 9 esetén csak egy.
21. Hófehérke a törpék kerek asztalánál névtáblákkal megjelölte mind a hét törpe helyét. Kuka érkezett elsőként, de figyelmetlenségből nem a helyére, hanem az óramutató járása szerint következő szomszédos helyre, Szundi helyére ült. Ezután, ha jött egy törpe, megkereste a helyét, és ha az üres volt, akkor elfoglalta, ha pedig már ült ott törpe, akkor az óramutató járását követve tovább ment az asztal körül, és leült az első szabad székre. Így hányféle ülésrend alakulhat ki?
Megoldás. A válasz: 32.
Két törpe, Kuka és Szundi biztos, hogy rossz helyre, más helyére ült. A többi törpénél választhatunk, hogy a szerencsések közé tartozik, vagy sem. Egy törpe szerencsés, ha a számára kijelölt helyre ül.
A szerencsés törpék csoportját 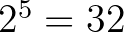 -féleképp állíthatjuk össze.
-féleképp állíthatjuk össze.
Ha a törpék leültek az asztal köré, akkor adott, hogy kik tartoznak a szerencsés csoportba. Ez fordítva is meghatározott, ha kiválasztottuk a szerencsés csoportot, akkor ahhoz tartozik egy ülésrend. Ebből adódik, hogy a szerencsés csoportok száma azonos az ülésrendek számával.
Válasszunk egy szerencsés csoportot és keressük meg, milyen ültetési sorrend tartozik hozzájuk. A törpék másik csoportja a balszerencsések csoportja. Előbb a szerencséseket ültetjük le, majd jönnek a balszerencsések. Legyenek balszerencsések Szundi, Kuka, Tudor és Vidor, székük ebben a sorrendben követi egymást az asztal körül az óramutató járása szerint haladva. Kuka és a szerencsés törpék már helyet foglaltak. Érkezik Szundi, a helyén Kuka ül, ezért megy tovább az asztal körül, és leül az első szabad helyre, Tudor helyére. Jön Tudor, leül Vidor helyére, majd Vidor érkezik, aki Szundi helyére ül.
Általánosítás. Dombi Péter a következőket írta: A lehetséges sorrendek száma 32, 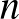 törpe esetén
törpe esetén 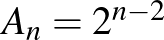 .
.
Bizonyítás. Legyen az utolsó, Kuka előtti hely Z részére fenntartva. Két esetet érdemes szétválasztani.
 Ha Z utolsónak megy asztalhoz, akkor egy kivétellel minden hely hézagmentesen fel lesz töltve az óramutató járása szerint, ezért Z az utolsó szabadon hagyott székre, Kuka helyére kerül. A lehetséges sorrendek száma így megegyezik a maradék 6 törpe által produkálható sorrendek számával, jelöljük ezt
Ha Z utolsónak megy asztalhoz, akkor egy kivétellel minden hely hézagmentesen fel lesz töltve az óramutató járása szerint, ezért Z az utolsó szabadon hagyott székre, Kuka helyére kerül. A lehetséges sorrendek száma így megegyezik a maradék 6 törpe által produkálható sorrendek számával, jelöljük ezt 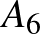 -tal.
-tal.
 Ha Z nem az utolsó, akkor amikor asztalhoz indul, még legalább két szék üres, és nyilván az asztal „végén", tehát Z a saját helyére fog ülni. Ilyen esetekben tehát Z széke a többi törpe számára nem létezik, így ismét csak
Ha Z nem az utolsó, akkor amikor asztalhoz indul, még legalább két szék üres, és nyilván az asztal „végén", tehát Z a saját helyére fog ülni. Ilyen esetekben tehát Z széke a többi törpe számára nem létezik, így ismét csak 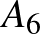 különböző sorrend alakulhat ki.
különböző sorrend alakulhat ki.
Ezt minden lépésre elmondva 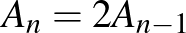 , és így
, és így 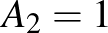 ,
, 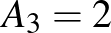 stb. miatt
stb. miatt 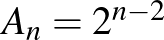 adódik.
adódik.
Lábjegyzetek
- 1 Varga Tamás: Matematika lexikon (Műszaki Kiadó, SHL Hungary, 2001) c. könyvében a 300. oldalon ezt olvassuk: „Négyzetszám egész szám négyzete. A legkisebb négyzetszám a 0, a többi mind pozitív.” A Freud–Gyarmati: Számelmélet c. könyv is négyzetszámnak tekinti a nullát. Így szól a 7.7.3. Lemma: Két (nemnulla) négyzetszám összege és különbsége nem lehet egyszerre négyzetszám.
- 2 A fenti, különlegesen szép gondolatmenet tudomásom szerint Laczkovich Miklóstól származik – írja Dombi Péter. Laczkovich Miklós azonban úgy emlékszik, Kós Gézától hallotta a feladat különböző változatait és azok elegáns bizonyítását.
- 3 Érdemes megkeresni az F3220-as feladatot a KöMaL archívumában, a http://db.komal.hu/KomalHU/ oldalon. Ebben 10 x 10-es tábla 9 parcellája gazos, kérdés, hogy az egész mező elgazosodik-e? Gyenes Zoltán (akkor 10. o. tanuló) megoldása az 1999. januári számban jelent meg, a fentihez hasonló meggondolással belátja, hogy 9 esetén nem, de 10 parcellánál már elgazosodhat a mező.
Róka Sándor, a Héttusa rovat szerkesztője











